Tailieumoi.vn xin giới thiệu đến các quý thầy cô Giáo án Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn (2022) - Toán 9 theo mẫu Giáo án môn Toán học chuẩn của Bộ Giáo dục. Hi vọng tài liệu này sẽ giúp thầy/cô dễ dàng biên soạn chi tiết Giáo án môn Toán học lớp 9. Chúng tôi rất mong sẽ được thầy/cô đón nhận và đóng góp những ý kiến quý báu của mình.
Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

§5. GÓC CÓ ĐỈNH BÊN TRONG, BÊN NGOÀI ĐƯỜNG TRÒN
A. MỤC TIÊU:
1.Kiến thức: HS nhận biết được góc có đỉnh ở bên trong hay bên ngoài đường tròn. Biết cách tính số đo của góc đó.
2 Kỹ năng: Vận dụng được các định lí để chứng minh các bài tập
Rèn luyện kỹ năng vẽ hình, phân tích, chứng minh thông qua các bài tập. Biết vận dụng các tính chất trên vào bài tập dựng hình, bài toán thực tế.
3 Thái độ: Cẩn thận, tập trung, chú ý
4 Xác định nội dung trọng tâm. HS nhận biết được góc có đỉnh ở bên trong hay bên ngoài đường tròn. Biết cách tính số đo của góc đó. Vận dụng được các định lí để chứng minh các bài tập
5- Định hướng phát triển năng lực:
-Năng lực chung: tự học, giải quyết vấn đề, tư duy, tự quản.
-Năng lưc chuyên biệt. Biết Vận dụng được các định lí để chứng minh các bài tập, bài toán thực tế.
B. PHƯƠNG PHÁP, KĨ THUẬT, HÌNH THỨC TỔ CHỨC DẠY HỌC:
- Phương pháp và kĩ thuật dạy học: Đàm thoại gợi mở, thuyết trình,..,
- Hình thức tổ chức dạy học: Cá nhân, nhóm.
- Phương tiện và thiết bị dạy học: Thước, bảng phụ, MTBT.
C. CHUẨN BỊ:
1. Giáo viên: Thước thẳng, bảng phụ, phấn màu
2. Học sinh: Thực hiện hướng dẫn tiết trước
D. MÔ TẢ MỨC ĐỘ NHẬN THỨC:
1. Bảng mô tả 4 mức độ nhận thức:
|
Cấp độ Chủ đề |
Nhận biết M1 |
Thông hiểu M2 |
Vận dụng M3 |
Vận dụng cao M4 |
|
góc có đỉnh ở bên trong đường tròn -góc có đỉnh ở bên ngoài đường tròn |
K/niệm góc có đỉnh ở bên trong đường tròn -góc có đỉnh ở bên ngoài đường tròn. |
Phát biểu định lý và hệ quả về Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn. |
Vận dụng định nghĩa, định lý và hệ quả Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn giai bài tập áp dụng. Làm bài tập 37 tr 82 sgk : |
chứng minh đc định lý Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn. |
E. TIẾN TRÌNH TIẾT DẠY:
1. Ổn định lớp:
2. Kiểm tra bài cũ: (không kiểm tra)
3. Khởi động:
|
Hoạt động của giáo viên |
Hoạt động của học sinh |
|
Gv đưa mô hình về góc ở tâm, góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung. Sau đó Gv dời đỉnh của góc ra ngoài và vào trong đường tròn. Yêu cầu Hs nêu dự đoán tên gọi của góc |
Hs nêu dự đoán |
|
Mục tiêu: Bước đầu Hs làm quen với khái niệm góc có đỉnh bên trong, bên ngoài đường tròn. Phương pháp và kĩ thuật dạy học: Đàm thoại gợi mở, thuyết trình,... Hình thức tổ chức dạy học: Cá nhân, nhóm. Phương tiện và thiết bị dạy học: Thước, bảng phụ, MTBT. Sản phẩm: Dự đoán của học sinh |
|
4. Hoạt động hình thành kiến thức:
|
HOẠT ĐỘNG CỦA GV VÀ HS |
NỘI DUNG |
||
|
Hoạt động 1: Góc có đỉnh ở bên trong đường tròn – cá nhân + cặp đôi Mục tiêu: Hs phát biểu được đ.n góc có đỉnh bên trong đường tròn, chứng minh được định lý 1 Phương pháp và kĩ thuật dạy học: Đàm thoại gợi mở, thuyết trình,... Hình thức tổ chức dạy học: Cá nhân, nhóm. Phương tiện và thiết bị dạy học: Thước, bảng phụ, MTBT. Sản phẩm: Đ.n và tính chất của góc có đỉnh bên trong đường tròn. NLHT: NL tự học, hợp tác, sử dụng công cụ vẽ. |
|||
|
Bước 1: Gv Vẽ hình và giới thiệu góc có đỉnh bên trong đường tròn. Qui ước cung bị chắn H. chắn những cung nào ? H. Góc ở tâm có phải là góc có đỉnh ở bên trong đường tròn không ? GV. Gọi HS đọc to định lí GV. Gợi ý c/m : TaÏo ra các góc nội tiếp chắn GV. Gọi một HS c/m
GV. Yêu cầu HS làm BT 36 tr 82 SGK GV. Phân tích đi lên AEH cân
GV. Yêu cầu HS hoạt động nhóm từ 3 đến 4 phút GV. Gọi một HS đại diện nhóm trình bày bài giải GV. Đưa các hình 33, 34, 35 lên bảng phụ và giới thiệu góc có đỉnh ở bên ngoài đường tròn. Bước 2: Gv chốt lại vấn đề. |
1. Góc có đỉnh ở bên trong đường tròn : *KN: Gọi là góc có đỉnh ở bên trong đường tròn (O) chắn hai cung và
* Định lí : (sgk) ?1 Nối D với B. Theo định nghĩa góc nội tiếp ta có: Mà (góc ngoài của tam giác ) |
||
|
Hoạt động 2: Góc có đỉnh ở bên ngoài đường tròn – Cá nhân + Nhóm Mục tiêu: Hs phát biểu được đ.n góc có đỉnh bên ngoài đường tròn, chứng minh được định lý 2 Phương pháp và kĩ thuật dạy học: Đàm thoại gợi mở, thuyết trình,... Hình thức tổ chức dạy học: Cá nhân, nhóm. Phương tiện và thiết bị dạy học: Thước, bảng phụ, MTBT. Sản phẩm: Đ.n và tính chất của góc có đỉnh bên ngoài đường tròn. NLHT: NL tự học, hợp tác, sử dụng công cụ vẽ. |
|||
|
Hoạt động 2 (20p)
GV. Gọi HS đọc định lí sgk H. Với nội dung đ/l ta cần c/m điều gì ? GV. Cho HS c/m từng trường hợp - TH 1 : Hai cạnh của góc là cát tuyến. - TH 2 : Một cạnh của góc là cát tuyến, 1 cạnh là tiếp tuyến. - TH 3 : Hai cạnh đều là tiếp tuyến. GV. Gợi ý tạo ra các góc nội tiếp trong trường hợp 1
GV. TH 2 và TH 3 học sinh về nhà c/m Góc có đỉnh ở bên ngoài đường tròn |
2. Góc có đỉnh ở bên ngoài đường tròn :
*KN:Góc có đỉnh ở bên ngoài đường tròn là góc: - Có đỉnh nằm ngoài đường tròn. - Các cạnh đều có điểm chung với đường tròn ( có 1 hoặc 2 điểm chung ) *ĐL: ?2 C/m : TH 1 : Nối A và C. Ta có là góc ngoài của tam giác AEC Mặt khác : (định lí góc nt ) |
||
4. Câu hỏi và bài tập củng cố - Hướng dẫn về nhà:
a. Câu hỏi và bài tập củng cố
C1. Nhắc lại định lí góc có đỉnh ở bên trong đường tròn và góc có đỉnh ở bên ngoài đường tròn.(M2)
C2.Làm bài tập 37 tr 82 sgk :.(M3)
Ta có
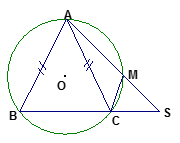 |
sđ (đ/l góc có đỉnh ở bên ngoài đường tròn)
( đ/l góc nội tiếp )
Mà AB = AC (gt) . Vậy
b. Hướng dẫn về nhà
Về nhà hệ thống các loại góc với đường tròn.
Biết áp dụng các định lí.làm các bài tập 38.39.40 SGK. Chuẩn bị tiết sau luyện tập.



