Bài 4.25 trang 84 Toán lớp 7: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.

a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.

b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.

Phương pháp giải:

Lời giải:

a)

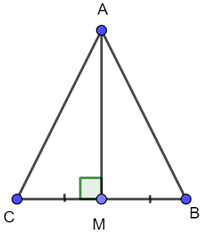
Xét 2 tam giác vuông AMC và AMB có:

AM chung

BM=CM (gt)

=>$\mathrm{\Delta }AMB=\mathrm{\Delta }AMC$ (c.g.c)

=> AM=BM (2 cạnh tương ứng)

=> Tam giác ABM cân tại A

b)

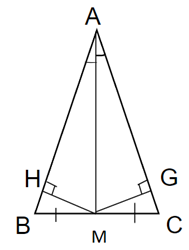
Kẻ MH vuông góc với AB(H thuộc AB)

     MG vuông góc với AC (G thuộc AC)

Xét 2 tam giác vuông AHM và AGC có:

$\widehat{HAM}=\widehat{GAM}$

AM chung

=>$\mathrm{\Delta }AHM=\mathrm{\Delta }AGC$(cạnh huyền – góc nhọn)

=>HM=GM (2 cạnh tương ứng)

Xét 2 tam giác vuông BHM và CGM có:

BM=CM(gt)

MH=MG(cmt)

=>$\mathrm{\Delta }BHM=\mathrm{\Delta }CGM$(cạnh huyền – cạnh góc vuông)

=>$\widehat{BMH}=\widehat{CMH}$(2 góc tương ứng)

=>Tam giác ABC cân tại A.

Bài tập vận dụng:

Bài 1. Cho tam giác ABC cân tại A. Kẻ BH và CK lần lượt vuông góc với AC và AB (H ∈ AC; K ∈ AB). Chứng minh rằng BH = CK.

Hướng dẫn giải

Xét tam giác BHA (vuông tại H) và tam giác CKA (vuông tại K) có:

AB = AC ($\Delta ABC$ cân tại A)

$\hat{A}$ là góc chung

⇒ $\Delta BHA=\Delta CKA$ (cạnh huyền – góc nhọn)

⇒ BH = CK (hai cạnh tương ứng)

Vậy BH = CK (đpcm).

Bài 2. Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC. Chứng minh AI vuông góc với BC và AI là tia phân giác của góc BAC.

Hướng dẫn giải

Xét tam giác AIB và tam giác AIC có:

AB = AC ($\Delta ABC$ cân tại A)

BI = CI (theo giả thiết)

AI là cạnh chung

⇒ $\Delta AIB=\Delta AIC$ (c.c.c)

⇒ $\widehat{AIB}=\widehat{AIC}$ (hai góc tương ứng)

Mà $\widehat{AIB}+\widehat{AIC}=180°$

⇒ $\widehat{AIB}=\widehat{AIC}=90°$

⇒ AI ⊥ BC (đpcm)

Vì $\Delta AIB=\Delta AIC$ (chứng minh trên)

⇒ $\widehat{IAB}=\widehat{IAC}$ (hai góc tương ứng)

⇒ AI là tia phân giác của góc BAC (đpcm).

Bài 3. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân.

Hướng dẫn giải

$\Delta ABC$ cân tại A ⇒ $\widehat{ABC}=\widehat{ACB}$ (tính chất)

Mà: $\widehat{ABC}+\widehat{ABD}=180°$ (hai góc kề bù)

$\widehat{ACB}+\widehat{ACE}=180°$ (hai góc kề bù)

Do đó, $\widehat{ABD}=\widehat{ACE}$

Xét tam giác ADB và tam giác AEC có:

AB = AC ($\Delta ABC$ cân tại A)

$\widehat{ABD}=\widehat{ACE}$ (chứng minh trên)

BD = CE (theo giả thiết)

⇒ $\Delta ADB=\Delta AEC$ (c.g.c)

⇒ AD = AE (hai cạnh tương ứng)

⇒ $\Delta ADE$ cân tại A (đpcm).