Với giải HĐ 4 trang 72 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
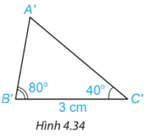
HĐ 4 trang 72 Toán lớp 7: Vẽ thêm tam giác sao cho , .
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và .
Hai tam giác A B C và có bằng nhau không?
Phương pháp giải:
Dùng thước thẳng hoặc compa để đo độ dài các cạnh của 2 tam giác và so sánh
Lời giải:
Tương tự Hoạt động 3, ta vẽ hình như sau:
Bước 1. Vẽ đoạn thẳng B'C' = 3cm
Bước 2. Dùng thước đo độ, vẽ hai tia B'x' và C'y' sao cho x'B'C' = 80 độ, y'C'B' = 40 độ
Bước 3. Lấy giao điểm A' của hai tia B'x' và C'y' ta được tam giác A'B'C'.
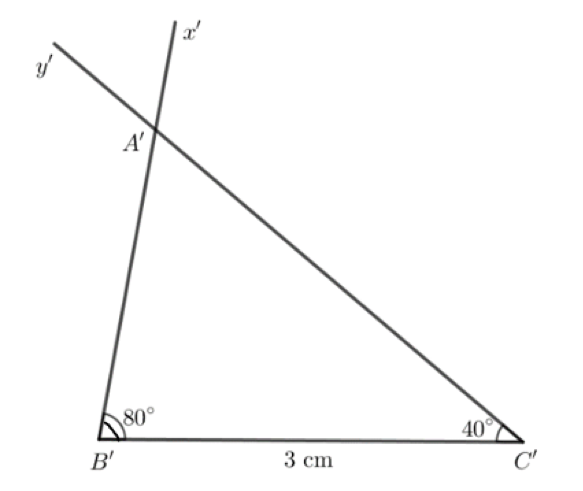
- Dùng thước thẳng có vạch chia, ta đo được AB = A'B' 2,2 cm; AC = A'C' 3,4 cm và BC = B'C' = 3 cm
- Xét hai tam giác ABC và A'B'C' có:
AB = A'B' (chứng minh trên).
ABC = A'B'C' (cùng bằng 80o).
BC = B'C' (chứng minh trên).
Vậy (c – g – c).
Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g)
• Trong tam giác ABC, hai góc ABC, ACB (hay góc B và góc C) được gọi là hai góc kề cạnh BC của tam giác ABC.
• Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ
+ Tam giác ABC và tam giác EFD có ; ; góc B và góc C là hai góc kề của cạnh BC, góc F và góc D là hai góc kề của cạnh FD; cạnh BC = FD = 6cm.
Khi đóta có <theo trường hợp góc cạnh góc (g.c.g)
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác