Với giải Luyện tập 3 trang 77 Toán 9 Tập 2 Cánh diều chi tiết trong Bài 2: Tứ giác nội tiếp đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp đường tròn

Luyện tập 3 trang 77 Toán 9 Tập 2: Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8 cm và 6 cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.

Lời giải:

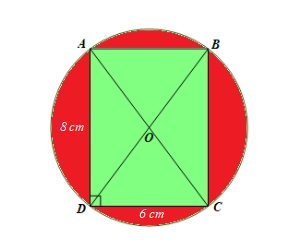
Giả sử hình chữ nhật ABCD nội tiếp đường tròn (O) có AB = CD = 6 cm và AD = BC = 8 cm.

Khi đó đường chéo AC là đường kính của đường tròn (O).

Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:

AC² = AD² + DC² = 8² + 6² = 100.

Suy ra AC = 10 cm.

Do đó bán kính của đường tròn (O) là $R=\frac{AC}{2}=\frac{10}{2}=5\text{ (cm).}$

Diện tích hình tròn bán kính R = 5 cm là:

S₁ = πR² = π.5² = 25π (cm²).

Diện tích hình chữ nhật ABCD là:

S₂ = AD.DC = 8.6 = 48 (cm²).

Diện tích phần được tô màu đỏ là:

S = S₁ – S₂ = 25π – 48 (cm²) ≈ 30,5 (cm²) với π ≈ 3,14.