Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O)

Lữ Ngọc My My Ngày: 28-07-2024 Lớp 9

Với giải Thử thách 2 trang 89 Toán 9 Tập 2 Kết nối tri thức chi tiết trong Bài 30: Đa giác đều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 30: Đa giác đều

Thử thách nhỏ 2 trang 89 Toán 9 Tập 2: Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).

Lời giải:

Giả sử lục giác đều ABCDEF nội tiếp đường tròn (O) (hình vẽ).

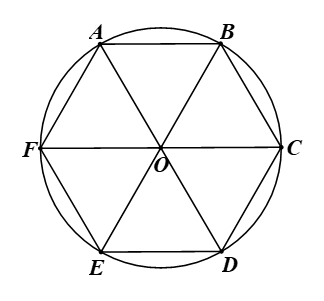
Thử thách nhỏ 2 trang 89 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

Vì lục giác ABCDEF nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OF.

Vì ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC.

Do đó ∆OAB = ∆OBC (c.c.c).

Chứng minh tương tự ta có

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOF = ∆FOA.

Suy ra $\hat{A O B} = \hat{B O C} = \hat{C O D} = \hat{D O E} = \hat{E O F} = \hat{F O A} .$

Mà $\hat{A O B} + \hat{B O C} + \hat{C O D} + \hat{D O E} + \hat{E O F} + \hat{F O A} = 360 °$

Do đó $6 \hat{A O B} = 360 °$

Suy ra $\hat{A O B} = \hat{B O C} = \hat{C O D} = \hat{D O E} = \hat{E O F} = \hat{F O A} = \frac{360 °}{6} = 60 ° .$

Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 60°.

Vậy mỗi phép quay thuận chiều 60° tâm O ở mỗi đỉnh A, B, C, D, E, F sẽ giữ nguyên lục giác đều nội tiếp đường tròn tâm O.

Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 84 Toán 9 Tập 2: Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:...

Câu hỏi trang 85 Toán 9 Tập 2: Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp đường tròn bán kính 2 cm (H.9.40) thì độ dài các cạnh của lục giác đều bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?...

Luyện tập 1 trang 86 Toán 9 Tập 2: Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?...

Thử thách nhỏ 1 trang 87 Toán 9 Tập 2: Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?...

HĐ2 trang 87 Toán 9 Tập 2: Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có dạng hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay có dạng hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều quay của kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B....

HĐ3 trang 87 Toán 9 Tập 2: Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến vị trí của điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?...

Câu hỏi trang 88 Toán 9 Tập 2:...

Luyện tập 2 trang 88 Toán 9 Tập 2: Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50....

Thực hành trang 88 Toán 9 Tập 2: Cho điểm O và điểm A khác điểm O (H.9.51)....

Thử thách nhỏ 2 trang 89 Toán 9 Tập 2: Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O)....