Với giải Luyện tập 1 trang 9 Chuyên đề Toán 12 Kết nối tri thức chi tiết trong Bài 1: Biến ngẫu nhiên rời rạc và các số đặc trưng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 12. Mời các bạn đón xem:

Giải Chuyên đề Toán 12 Bài 1: Biến ngẫu nhiên rời rạc và các số đặc trưng

Luyện tập 1 trang 9 Chuyên đề Toán 12: Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.

Lời giải:

Các giá trị của X thuộc tập {0; 1; 2; 3}.

Ta cần tính P(X = 0), P(X = 1), P(X = 2), P(X = 3).

Số kết quả có thể là $C_{16}^3=560$.

+) Biến cố (X = 0) là biến cố: “Chọn được 3 học sinh nữ”.

Số kết quả thuận lợi cho biến cố (X = 0) là $C_6^3=20$.

Vậy $P\left(X=0\right)=\frac{20}{560}=\frac{2}{56}$.

+) Biến cố (X = 1) là biến cố: “Chọn được 1 học sinh nam và 2 học sinh nữ”.

Có $C_{10}^1=10$ cách chọn 1 học sinh nam trong 10 học sinh nam và $C_6^2=15$ cách chọn 2 học sinh nữ trong 6 học sinh nữ.

Theo quy tắc nhân ta có 10.15 = 150 cách chọn 1 học sinh nam và 2 học sinh nữ.

Vậy số kết quả thuận lợi cho biến cố (X = 1) là 150.

Do đó P(X = 1) = $\frac{150}{560}=\frac{15}{56}$.

+) Biến cố (X = 2) là biến cố: “Chọn được 2 học sinh nam và 1 học sinh nữ”.

Có $C_{10}^2=45$ cách chọn 2 học sinh nam trong 10 học sinh nam và $C_6^1=6$ cách chọn 1 học sinh nữ trong 6 học sinh nữ. Theo quy tắc nhân ta có 45.6 = 270 cách chọn 2 học sinh nam và 1 học sinh nữ.

Vậy số kết quả thuận lợi cho biến cố (X = 2) là 270.

Do đó $P\left(X=2\right)=\frac{270}{560}=\frac{27}{56}$.

+) Biến cố (X = 3) là biến cố: “Chọn được 3 học sinh nam”.

Số kết quả thuận lợi cho biến cố (X = 3) là $C_{10}^3=120$.

Do đó $P\left(X=3\right)=\frac{120}{560}=\frac{12}{56}$.

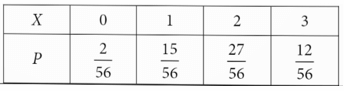
Vậy bảng phân bố xác suất của X là: