Tailieumoi.vn giới thiệu giải Chuyên đề học tập Toán lớp 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính sách Kết nối tri thức hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm Chuyên đề Toán 12. Mời các bạn đón xem:

Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính

Mở đầu trang 23 Chuyên đề Toán 12: Một xí nghiệp sản xuất hai loại sản phẩm I và II. Mỗi kilôgam sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ làm, đem lại mức lợi nhuận 40 nghìn đồng. Mỗi kilôgam sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ làm, đem lại mức lợi nhuận là 30 nghìn đồng. Xí nghiệp có 200 kg nguyên liệu và tối đa 1 200 giờ làm việc. Hãy đặt kế hoạch sản xuất để xí nghiệp có mức lợi nhuận cao nhất.

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.

Lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).

Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).

Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).

Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:

Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d₁: x + 2y = 100 và đường thẳng d₂: 2x + y = 80.

Các điểm cực biên là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).

Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền tứ giác OABC. Tính giá trị của F(x; y) tại các đỉnh của tứ giác, ta được:

F(0; 0) = 40.0 + 30.0 = 0;

F(0; 50) = 40.0 + 30.50 = 1 500;

F(20; 40) = 40.20 + 30.40 = 2 000;

F(40; 0) = 40.40 + 30.0 = 1 600.

Giá trị lớn nhất của F(x; y) bằng 2 000 tại (20; 40). Phương án tối ưu là (20; 40).

Vậy lợi nhuận cao nhất mà xí nghiệp đạt được là 2 000 nghìn đồng, tức 2 triệu đồng khi sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II.

1. Giới thiệu bài toán quy hoạch tuyến tính hai biến

HĐ1 trang 24 Chuyên đề Toán 12: Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.

a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y.

b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán.

c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác này.

d) Tính giá trị của F(x; y) tại các đỉnh của miền tứ giác tìm được trong ý b, từ đó dự đoán về mức lợi nhuận cao nhất.

Lời giải:

a) Lợi nhuận đem lại từ x kg sản phẩm loại I là 40x nghìn đồng.

Lợi nhuận đem lại từ y kg sản phẩm loại II là 30y nghìn đồng.

Vậy lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).

b) Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).

Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).

Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:

c) Miền nghiệm của hệ bất phương trình trong ý b là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d₁: x + 2y = 100 và đường thẳng d₂: 2x + y = 80.

A là giao điểm của đường thẳng d₁ với trục tung nên A(0; 50).

B là giao điểm của hai đường thẳng d₁ và d­₂ nên B(20; 40).

C là giao điểm của đường thẳng d₂ với trục hoành nên C(40; 0).

Vậy các đỉnh của miền nghiệm là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).

d) Ta có:

F(0; 0) = 40.0 + 30.0 = 0;

F(0; 50) = 40.0 + 30.50 = 1 500;

F(20; 40) = 40.20 + 30.40 = 2 000;

F(40; 0) = 40.40 + 30.0 = 1 600.

Dự đoán mức lợi nhuận cao nhất là 2 000 nghìn đồng, hay 2 triệu đồng.

Luyện tập 1 trang 26 Chuyên đề Toán 12: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất X và 9 kg chất Y. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất X và 0,6 kg chất Y. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất X và 1,5 kg chất Y. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.

Phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đáp ứng được các yêu cầu đặt ra ở trên?

a) Đặt ẩn và viết bài toán quy hoạch tuyến tính diễn tả yêu cầu của bài toán trên.

b) Biểu diễn tập các phương án chấp nhận được và tìm các phương án cực biên.

Lời giải:

a) Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng (x ≥ 0, y ≥ 0).

Do cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên x ≤ 10, y ≤ 9.

Số kg chất X chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 20x + 10y (kg).

Số kg chất Y chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 0,6x + 1,5y (kg).

Theo bài, cần chiết xuất ít nhất 140 kg chất X và 9 kg chất Y nên ta có hệ phương trình:

Gọi F(x; y) là chi phí mua nguyen liệu, khi đó F(x; y) = 4x + 3y (triệu đồng).

Vậy ta có bài toán quy hoạch tuyến tính như sau:

F(x; y) = 4x + 3y → min

với các ràng buộc

b) Tập các phương án chấp nhận được là miền tô màu trong hình vẽ dưới đây:

Các đỉnh của miền nghiệm là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).

Các phương án cực biên là: (2,5; 9), (10; 9), (10; 2), (5; 4).

2. Bài toán quy hoạch tuyến tính với miền chấp nhận được là miền đa giác

HĐ2 trang 26 Chuyên đề Toán 12: Ta giải bài toán Tình huống mở đầu.

Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau: F(x; y) = 40x + 30y → max

Với các ràng buộc

Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3.

a) Tìm tập hợp các điểm M(x; y) thỏa mãn F(x; y) = 40x + 30y = 1 200.

b) Với mỗi số thực m xét đường thẳng d_m­: 40x + 30y = m.

Từ hình vẽ, tìm điều kiện của m để d_m ∩ S ≠ ∅.

c) Từ câu b suy ra giá trị lớn nhất của F(x; y) trên miền S, từ đó suy ra lời giải của bài toán.

Lời giải:

a) Theo bài, F(x; y) = 40x + 30y = 1 200, hay 4x + 3y = 120.

Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d₁₂₀₀: 4x + 3y = 120 nằm trong miền chấp nhận S, chính là tập hợp các điểm nằm trên đoạn thẳng AB (hình vẽ).

b) Đường thẳng d_m song song với AB, có phương không đổi, do đó từ hình vẽ, ta thấy đường thẳng d_m: 40x + 30y = m luôn cắt trục tung tại điểm có tung độ $y=\frac{m}{30}.$

Từ hình vẽ, ta thấy rằng để d_m ∩ S ≠ ∅ thì $0\le \frac{m}{30}\le \frac{200}{3}$ tức là 0 ≤ m ≤ 2 000.

Vậy 0 ≤ m ≤ 2 000.

c) Ta có: F(x; y) = 40x + 30y = m, mà theo kết quả của câu b, ta có 0 ≤ m ≤ 2 000 nên 0 ≤ F(x; y) ≤ 2 000.

Vậy giá trị lớn nhất của F(x; y) trên miền S là 2 000.

Ta có lời giải của bài toán như sau:

Gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.

Lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).

Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).

Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).

Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:

Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d₁: x + 2y = 100 và đường thẳng d₂: 2x + y = 80.

Xét đường thẳng d_m: 40x + 30y = m luôn cắt trục tung tại điểm có tung độ $y=\frac{m}{30}.$

Từ hình vẽ, ta thấy rằng để d_m ∩ S ≠ ∅ thì $0\le \frac{m}{30}\le \frac{200}{3}$ tức là 0 ≤ m ≤ 2 000.

Ta có: F(x; y) = 40x + 30y = m, nên 0 ≤ F(x; y) ≤ 2 000.

Giá trị lớn nhất của F(x; y) trên miền S là 2 000.

Vậy lợi nhuận cao nhất mà xí nghiệp đạt được là 2 000 nghìn đồng, tức 2 triệu đồng khi sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II.

Luyện tập 2 trang 29 Chuyên đề Toán 12: Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?

Lời giải:

Gọi x và y lần lượt là số xe loại A và loại B cần thuê.

Chi phí thuê xe là: F(x; y) = 4x + 3y (triệu đồng).

Hệ bất phương trình ràng buộc x và y là:

Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD trong hình vẽ dưới đây:

Các điểm cực biên là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền tứ giác ABCD. Ta biết rằng F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị củ F(x; y) tại các đỉnh của tứ giác ta được:

F(2,5; 9) = 4.2,5 + 3.9 = 37;

F(10; 9) = 4.10 + 3.9 = 67;

F(10; 2) = 4.10 + 3.2 = 46;

F(5; 4) = 4.5 + 3.4 = 32.

Giá trị nhỏ nhất của F(x; y) bằng 32 tại D(5; 4). Phương án tối ưu là (5; 4).

Vậy phải thuê 5 xe loại A và 4 xe loại B để chi phí bỏ ra là ít nhất (32 triệu đồng) mà vẫn chở được hết hàng và người.

3. Bài toán quy hoạch tuyến tính với miền chấp nhận được không là miền đa giác

HĐ3 trang 29 Chuyên đề Toán 12: Xét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min

với các ràng buộc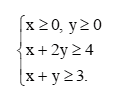 

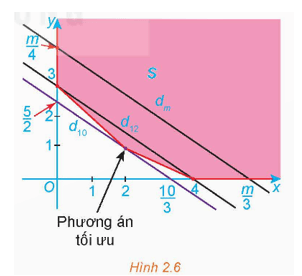
a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.

b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12.

c) Với mỗi số thực m, xét đường thẳng d_m: 3x + 4y = m.

Từ hình vẽ, tìm điều kiện của m để d_m ∩ S ≠ ∅.

d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận được. Chứng tỏ rằng, giá trị nhỏ nhất này chính là giá trị của F(x; y) tại một điểm cực biên của miền chấp nhận được.

Lời giải:

a) Biểu diễn miền nghiệm của các bất phương trình trong hệ ràng buộc ta thấy rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.

b) Theo bài, F(x; y) = 3x + 4y = 12.

Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d₁₂: 3x + 4y = 12 nằm trong miền chấp nhận S, chính là tập hợp các điểm nằm trên đoạn thẳng AB (hình vẽ).

b) Đường thẳng d_m song song với AB, có phương không đổi, do đó từ hình vẽ, ta thấy đường thẳng d_m: 3x + 4y = m luôn cắt trục tung tại điểm có tung độ $y=\frac{m}{4}.$

Từ hình vẽ, ta thấy rằng để d_m ∩ S ≠ ∅ thì $\frac{m}{4}\ge \frac{5}{2},$ tức là m ≥ 10.

Vậy m ≥ 10.

c) Ta có: F(x; y) = 3x + 4y = m, mà theo kết quả của câu b, ta có m ≥ 10 nên F(x; y) ≥ 10.

Vậy giá trị nhỏ nhất của F(x; y) trên miền S là 10.

Ta có các điểm cực biên của miền S là: (0; 3), (2; 1), (4; 0).

⦁ F(0; 3) = 3.0 + 4.3 = 12;

⦁ F(2; 1) = 3.2 + 4.1 = 10;

⦁ F(4; 0) = 3.4 + 4.0 = 12.

Vậy giá trị nhỏ nhất của F(x; y) trên miền S chính là giá trị của F(x; y) tại điểm cực biên có tọa độ (2; 1) của miền chấp nhận được.

Luyện tập 3 trang 32 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính sau: F(x; y) = x + 2y → min

với các ràng buộc

Lời giải:

Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:

Ở đây, d­­₁, d₂ là các đường thẳng có phương trình lần lượt là x + y = 1 và 2x + 4y = 3.

Có ba điểm cực biên là A(0; 1), B(0,5; 0,5), C(1,5; 0).

Với mỗi số thực m, xét đường thẳng d_m: x + 2y = m.

Đường thẳng d_m song song với đường thẳng d₂ (hay BC) và cắt Oy tại điểm $\left(0;\frac{m}{2}\right).$ Dễ thấy d_m ∩ S ≠ 0 nếu và chỉ nếu $\frac{m}{2}\ge 0,75,$ hay m ≥ 1,5.

Từ đó suy ra, giá trị nhỏ nhất của G(x; y) bằng 1,5, đạt được tại mọi điểm của đoạn BC.

Thực tế, mọi điểm M (x; y) thuộc đoạn BC ta đều có:

$F\left(x;y\right)=x+2y=\frac{1}{2}\left(2x+4y\right)=\frac{1}{2}\cdot 3=1,5.$

Cũng từ kết quả d_m ∩ S ≠ 0 nếu và chỉ nếu m ≥ 1,5 suy ra F(x; y) không có giá trị lớn nhất trên miền S. Thực tế, F(x; y) có thể lớn tùy ý khi x, y đủ lớn.

Vận dụng trang 32 Chuyên đề Toán 12: Một chủ trang trại cần sử dụng phân bón để chăm sóc cho một loại đậu tương. Loại đậu tương này cần ít nhất 18 đơn vị đạm và ít nhất 6 đơn vị phosphate. Ông chủ trang trại có thể sử dụng hai loại phân bón X và Y. Giá cả, hàm lượng đạm và hàm lượng phosphate có trong một tạ phân X và một tạ phân Y được cho bởi bảng sau:

Hãy cho biết cần phải mua bao nhiêu tạ phân loại X, bao nhiêu tạ phân loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên?

Lời giải:

Gọi x, y lần lượt là số tạ phân bón loại X là Y cần phải mua.

Chi phí mua phân bón là: F(x; y) = 1,7x + 1,2y (triệu đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm của hệ bất phương trình này là miền tô màu, không là miền đa giác (hình vẽ).

Ở đây, d₁: x + 3y = 9 và d₂: 2x + y = 6.

Các điểm cực biên là: A(0; 6), B(1,8; 2,4), C(9; 0).

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên theo phần Nhận xét ở trên thì F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Tính giá trị của F(x; y) tại các điểm cực biên ta được:

F(0; 6) = 1,7.0 + 1,2.6 = 7,2;

F(1,8; 2,4) = 1,7.1,8 + 1,2.2,4 = 5,94;

F(9; 0) = 1,7.9 + 1,2.0 = 15,3.

Do đó giá trị nhỏ nhất của F(x; y) bằng 5,94 tại điểm cực biên B(1,8; 2,4).

Vậy cần phải mua 1,8 tạ phân bón loại X và 2,4 tạ phân bón loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên.

Bài tập

Bài 2.1 trang 32 Chuyên đề Toán 12: Một trung tâm tổ chức sự kiện có một phòng tổ chức lễ cưới với hai kiểu bàn ăn: bàn hình chữ nhật ngồi 6 người với giá thuê 200 nghìn đồng và bàn tròn ngồi 10 người với giá thuê 300 nghìn đồng. Anh Nam muốn thuê phòng để tổ chức đám cưới với 250 khách mời. Căn phòng chỉ chứa được tối đa 35 bàn các loại và chỉ có 15 bàn hình chữ nhật. Hỏi anh Nam phải thuê mỗi loại bàn bao nhiêu để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.

Lời giải:

Gọi x và y lần lượt là số bàn hình chữ nhật và số bàn tròn cần thuê.

Chi phí thuê bàn là: 200x + 300y (nghìn đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu như hình vẽ dưới đây:

Ở đây, d₁: x + y = 35 và d₂: 3x + 5y = 125.

Các điểm cực biên là: A(0; 35), B(0; 25), C(15; 16), D(15; 20).

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên ta được:

F(0; 35) = 200.0 + 300.35 = 10 500;

F(0; 25) = 200.0 + 300.25 = 7 500;

F(15; 16) = 200.15 + 300.16 = 7 800;

F(15; 20) = 200.15 + 300.20 = 9 000.

Giá trị nhỏ nhất của F(x; y) bằng 7 500 tại điểm cực biên B(0; 25). Phương án tối ưu là (0; 25).

Vậy anh Nam chỉ cần thuê 25 bàn tròn để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.

Bài 2.2 trang 32 Chuyên đề Toán 12: Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này là dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng:

Nguồn nguyên liệu dự trữ dâu tây, sữa và đường lần lượt là 1,2 tấn; 0,8 tấn và 0,3 tấn. Giá bán mỗi đơn vị sữa chua X và Y lần lượt là 800 nghìn đồng và 1,2 triệu đồng. Cơ sở sản xuất cần sản xuất bao nhiêu đơn vị sữa chua X và Y để lợi nhuận thu được là lớn nhất?

Lời giải:

Đổi 800 nghìn đồng = 0,8 triệu đồng;

1,2 tấn = 1 200 kg; 0,8 tấn = 800 kg; 0,3 tấn = 300 kg.

Gọi x và y lần lượt là số đơn vị sữa chua X và Y cần sản xuất.

Lợi nhuận thu được là: 0,8x + 1,2y (triệu đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:

Ở đây, d₁: 2x + 3y = 1 200 và d₂: 2x + y = 800.

Các điểm cực biên là: O(0; 0), A(0; 300), B(150; 300), C(300; 200), D(400; 0).

Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên.

Ta có đường thẳng d₁ (hay BC) có phương trình là 2x + 3y = 1 200, nên với mọi điểm M(x; y) thuộc đường thẳng BC ta đều có:

F(x; y) = 0,8x + 1,2y = 0,4(2x+ 3y) = 0,4 . 1 200 = 480.

Vậy biểu thức F(x; y) đạt giá trị lớn nhất bằng 480 tại mọi điểm M(x; y) thuộc đoạn thẳng BC. Như vậy bài toán có vô số phương án tối ưu, đó là tọa độ của tất cả các điểm thuộc đoạn thẳng BC.

Vậy cơ sở sản xuất cần sản xuất x đơn vị sữa chua X và $y=400-\frac{2}{3}x$ đơn vị sữa chua Y với 150 ≤ x ≤ 300 thì lợi nhuận thu được là lớn nhất.

Bài 2.3 trang 33 Chuyên đề Toán 12: Một nhà máy hoá chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm³ khí CO (carbon monoxide) và 6 dm³ khí SO₂ (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm³ khí CO và 3 dm³ khí SO₂ phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm³ khí CO và không quá 5 400 dm³ khí SO₂. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồng một đơn vị hợp chất X và 24 000 đồng một đơn vị hợp chất Y. Xác định số đơn vị hợp chất X và Y mỗi loại cần sản xuất trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.

Lời giải:

Gọi x và y lần lượt là số đơn vị hợp chất X và Y cần sản xuất.

Lợi nhuận thu được là: F(x; y) = 36 000x + 24 000y (đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm của hệ bất phương trình này là miền tứ giác OABC được tô màu như hình vẽ dưới đây:

Ở đây, d₁: x + 2y = 1 500 và d₂: 2x + y = 1 800.

Các điểm cực biên là: O(0; 0), A(0; 750), B(700; 400), C(900; 0).

Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên ta được:

F(0; 0) = 36 000.0 + 24 000.0 = 0;

F(0; 750) = 36 000.0 + 24 000.750 = 18 000 000;

F(700; 400) = 36 000.700 + 24 000.400 = 34 800 000;

F(900; 0) = 36 000.900 + 24 000.0 = 32 400 000.

Giá trị lớn nhất của F(x; y) bằng 34 800 tại điểm cực biên B(700; 400). Phương án tối ưu là (700; 400).

Vậy cần sản xuất 700 đơn vị hợp chất X và 400 đơn vị hợp chất Y trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.

Bài 2.4 trang 33 Chuyên đề Toán 12: Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F₁ và F₂; mỗi đơn vị F₁ giá 1 200 đồng và mỗi đơn vị F₂ giá 720 đồng. Mỗi đơn vị thức ăn F₁ chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F₂ chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế ăn hỗn hợp F₁ và F₂ sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.

Lời giải:

Gọi x và y lần lượt là chế ăn hỗn hợp F₁ và F₂.

Chi phí cho thức ăn là: 1 200x + 720y (đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm của hệ bất phương trình này là miền tô màu, không là miền đa giác (hình vẽ).

Ở đây, d₁: 2x + y = 400, d₂: x + 2y = 500 và d₃: x + y = 350.

Các điểm cực biên là: A(0; 400), B(50; 300), C(200; 150), D(500; 0).

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Tính giá trị của F(x; y) tại các điểm cực biên ta được:

F(0; 400) = 1 200.0 + 720.400 = 288 000;

F(50; 300) = 1 200.50 + 720.300 = 276 000;

F(200; 150) = 1 200.200 + 720.150 = 348 000;

F(500; 0) = 1 200.500 + 720.0 = 600 000.

Do đó giá trị nhỏ nhất của F(x; y) bằng 276 000 tại điểm cực biên B(50; 300).

Vậy để chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng thì cần 50 chế ăn loại F₁ và 300 chế ăn loại F₂.

Bài 2.5 trang 33 Chuyên đề Toán 12: Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960 đồng một gam và mỗi gam S2 có chứa 25 đơn vị V1, 10 đơn vị V2, 10 đơn vị V3 và 20 đơn vị V4. Hỏi cần phải thêm vào 100 gam thức ăn cho gà mỗi loại S1 và S2 bao nhiêu gam để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà?

Lời giải:

Gọi x, y lần lượt là số gam thức ăn loại S1 và S2 cần thêm vào 100 gam thức ăn cho gà.

Chi phí mua thức ăn là: F(x; y) = 720x + 960y (đồng).

Hệ bất phương trình ràng buộc x và y là

Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:

Ở đây, d₁: x + 5y = 10, d₂: 5x + 2y = 20, d₃: x + y = 6 và d₄: 7x + 4y = 36.

Các điểm cực biên là: A(0; 10),$B\left(\frac{4}{3};\frac{20}{3}\right),$ C(4; 2), D(5; 1), E(10; 0).

Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Tính giá trị của F(x; y) tại các điểm cực biên ta được:

F(0; 10) = 720.0 + 960.10 = 9 600;

$F\left(\frac{4}{3};\frac{20}{3}\right)=720\cdot \frac{4}{3}+960\cdot \frac{20}{3}=7360;$

F(4; 2) = 720.4 + 960.2 = 4 800;

F(5; 1) = 720.5 + 960.1 = 4 560;

F(10; 0) = 720.10 + 960.0 = 7 200.

Do đó giá trị nhỏ nhất của F(x; y) bằng 4 560 tại điểm cực biên D(5; 1).

Vậy cần phải thêm vào 100 gam thức ăn cho gà là 5 g loại S1 và 1 g loại S2 để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà.

Xem thêm các bài giải Chuyên đề học tập Toán 12 Kết nối tri thức hay, chi tiết khác: