Với giải Vận dụng 3 trang 81 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Đường tròn

Vận dụng 3 trang 81 Toán 9 Tập 1: Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.

Lời giải:

Hình 18a): Hai đường tròn ở ngoài nhau.

Hình 18b): Hai đường tròn tiếp xúc ngoài.

Hình 18c): Hai đường tròn cắt nhau.

 Lý Thuyết Vị trí tương đối của hai đường tròn

Chú ý: Nếu OO’ = 0 thì O trùng với O’. Hai đường tròn có tâm trùng nhau gọi là hai đường tròn đồng tâm.

Bảng tóm tắt vị trí tương đối của hai đường tròn phân biệt (O;R) và (O’; R’) với $R\ge R^{\prime }$

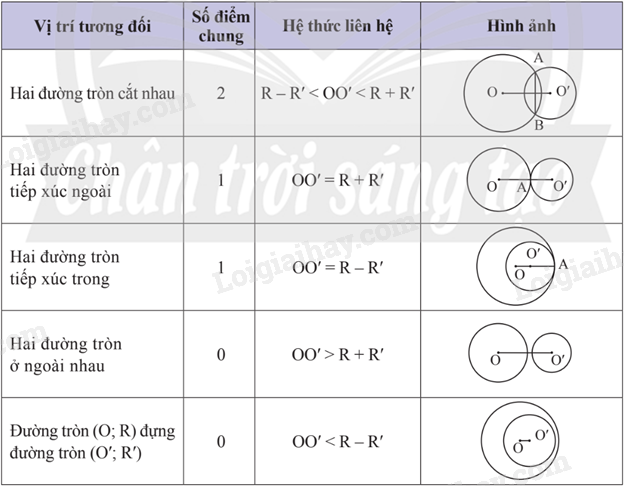
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:

4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.

Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.

Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.

Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có $O{O}^{\prime }>8cm$ thì $O{O}^{\prime }=8cm>3cm+4cm=R+R^{\prime }$ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.