Với giải Khám phá 2 trang 76 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Đường tròn
Khám phá 2 trang 76 Toán 9 Tập 1: a) Cho đường tròn (O; R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O; R). Tìm điểm B’ sao cho O là trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O; R) không? Giải thích.
b) Cho đường tròn (O; R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O; R) không? Giải thích.
Lời giải:
a)
i) Vì hai điểm A, A’ cùng nằm trên đường tròn (O; R) nên OA = OA’ = R.
Mà điểm O nằm giữa hai điểm A và A’ nên O là trung điểm của AA’.
ii) Vì O là trung điểm của BB’ nên OB = OB’ (tính chất trung điểm một đoạn thẳng).
Lại có điểm B thuộc đường tròn (O; R) nên OB = R. Do đó OB’ = R.
Vậy điểm B’ thuộc đường tròn (O; R).
b) Nối OM, OM’.
⦁ Trường hợp 1: Điểm M thuộc d thì điểm M’ trùng điểm M.
Mà điểm M thuộc đường tròn (O; R) nên điểm M’ thuộc đường tròn (O; R).
⦁ Trường hợp 1: Điểm M không thuộc d.
Vì đường trung trực d của đoạn thẳng MM’ đi qua điểm O nên O cách đều hai đầu mút hay OM = OM’.
Mà điểm M thuộc đường tròn (O; R) nên OM = R, do đó OM’ = R.
Vậy điểm M’ thuộc đường tròn (O; R).
Lý Thuyết Tính đối xứng của đường tròn
|
Đường tròn là hình có tâm đối xứng; tâm đối xứng là tâm của đường tròn. Đường tròn là hình có trục đối xứng. Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó. |
Ví dụ:
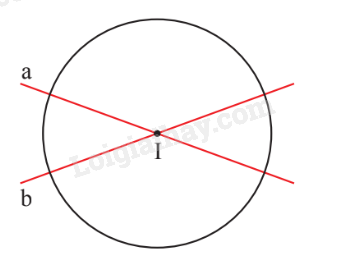
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Khám phá 2 trang 76 Toán 9 Tập 1: a) Cho đường tròn (O; R)........
Vận dụng 4 trang 81 Toán 9 Tập 1: Dùng compa đo bán kính và vẽ lại các hình trong Hình 19........
Bài 4 trang 82 Toán 9 Tập 1: Cho tứ giác ABCD có ........
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp