Với giải Khám phá 3 trang 77 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Đường tròn
Khám phá 3 trang 77 Toán 9 Tập 1: Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
a) Tính độ dài đoạn thẳng AB theo R.
b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.
Lời giải:
a) Vì hai điểm A, B cùng nằm trên đường tròn (O; R) nên OA = OB = R.
Mà AB đi qua O hay O nằm giữa A, B nên AB = OA + OB = R + R = 2R.
Vậy AB = 2R.
b) Xét ∆OMN có: OM + ON > MN (bất đẳng thức trong tam giác). (1)
Ta có hai điểm M, N cùng nằm trên đường tròn (O; R) nên OM = ON = R.
Do đó từ (1) ta có R + R > MN hay 2R > MN.
Mà AB = 2R (câu a) nên AB > MN.
Lý Thuyết Đường kính và dây cung của đường tròn
Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
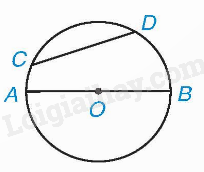
Quan hệ giữa dây và đường kính
|
Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất. |
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Khám phá 2 trang 76 Toán 9 Tập 1: a) Cho đường tròn (O; R)........
Vận dụng 4 trang 81 Toán 9 Tập 1: Dùng compa đo bán kính và vẽ lại các hình trong Hình 19........
Bài 4 trang 82 Toán 9 Tập 1: Cho tứ giác ABCD có ........
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
