Luyện tập 2 trang 13 Toán 9 Tập 1: Nêu hai nghiệm của phương trình: $6x-5y=11$.

Lời giải:

Hai nghiệm của phương trình đã cho là: $\left(1;-1\right);\left(2;\frac{1}{5}\right)$

Lý Thuyết Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn

Ví dụ: $2x+3y=4$, $0x+2y=3$, $x+0y=2$ là các phương trình bậc nhất hai ẩn.

Nghiệm của phương trình bậc nhất hai ẩn

Ví dụ: Cặp số $(-1;2)$ là nghiệm của phương trình $2x+3y=4$ vì $2.\left(-1\right)+3.2=-2+6=4$.

Cặp số $(1;2)$ không là nghiệm của phương trình $2x+3y=4$ vì

$2.1+3.2=2+6=8\ne 4$.

Chú ý:

Ta cũng áp dụng được quy tắc chuyển vế, quy tắc nhân đã biết ở phương trình bậc nhất một ẩn để biến đổi phương trình bậc nhất hai ẩn.

Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm của phương trình $ax+by=c$ được biểu diễn bởi một điểm. Nghiệm $\left(x_0;y_0\right)$ được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$.

- Mỗi nghiệm của phương trình $ax+0y=c\left(a\ne 0\right)$ được biểu diễn bởi điểm có tọa độ $\left(\frac{c}{a};y_0\right)$ $\left(y_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_1:x=\frac{c}{a}$. Đường thẳng $d_1$ là đường thẳng đi qua điểm $\frac{c}{a}$ trên trục Ox và vuông góc với trục Ox.

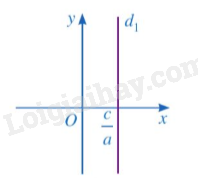
- Mỗi nghiệm của phương trình $0x+by=c\left(b\ne 0\right)$ được biểu diễn bởi một điểm có tọa độ $\left(x_0;\frac{c}{b}\right)\left(x_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_2:y=\frac{c}{b}$. Đường thẳng $d_2$ là đường thẳng đi qua điểm $\frac{c}{b}$ trên trục Oy và vuông góc với trục Oy.

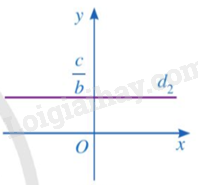
- Mỗi nghiệm của phương trình $ax+by=c\left(a\ne 0,b\ne 0\right)$ được biểu diễn bởi một điểm nằm trên đường thẳng $d_3:y=-\frac{a}{b}x+\frac{c}{b}$.

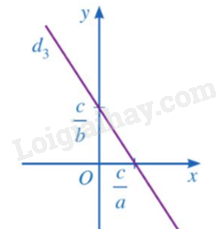
Ví dụ:

Nghiệm của phương trình $-3x+y=2$ được biểu diễn bởi đường thẳng d: $y=3x+2$.

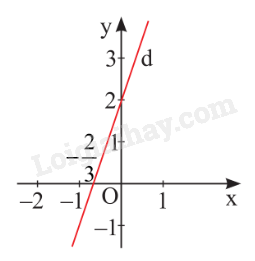
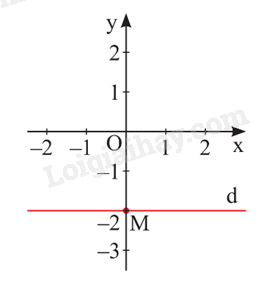
Nghiệm của phương trình $0x+y=-2$ được biểu diễn bởi đường thẳng d: $y=-2$ vuông góc với Oy tại điểm $M\left(0;-2\right)$.

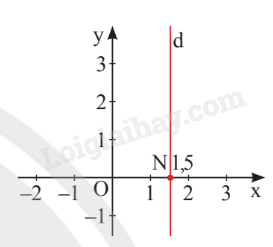
Nghiệm của phương trình $2x+0y=3$ được biểu diễn bởi đường thẳng d: $x=1,5$ vuông góc với Ox tại điểm $N\left(1,5;0\right)$.