Với giải sách bài tập Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Bài 9 trang 14 SBT Toán 9 Tập 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn x, y?

a) 2x + 7y = 15.

b) 0,7x² ‒ 0,5y² = 11.

c) x + 0y = 9.

Lời giải:

Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng ax + by = c, trong đó a, b, c là những số cho trước, a ≠ 0 hoặc b ≠ 0.

Do đó, phương trình ở các câu a, c là phương trình bậc nhất hai ẩn x, y.

Phương trình 0,7x² ‒ 0,5y² = 11 có chứa x² và y² nên không là phương trình bậc nhất hai ẩn x, y.

Bài 10 trang 14 SBT Toán 9 Tập 1: Cho phương trình bậc nhất hai ẩn x, y: 2x ‒ 3y = 5 (1)

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Cặp số (1; ‒1) là nghiệm duy nhất của phương trình (1).

b) Cặp số (4; 1) là một nghiệm của phương trình (1).

c) Cặp số (‒2; ‒3) không phải là nghiệm của phương trình (1).

Lời giải:

⦁ Phương trình bậc nhất hai ẩn x, y có vô số nghiệm (x; y), mỗi nghiệm được biểu diễn bởi một điểm nằm trên đường thẳng $y=-\frac{a}{b}x+\frac{c}{b}.$ Do đó phát biểu a) là sai.

⦁ Thay x = 4; y = 1 vào phương trình (1) ta có:

2.4 ‒ 3.1 = 5.

Suy ra, cặp số (4; 1) là một nghiệm của phương trình (1). Do đó phát biểu b) là đúng.

⦁ Thay x = ‒2; y = ‒3 vào phương trình (1) ta có:

2.(‒2) ‒ 3.(‒3) = 5.

Suy ra, cặp số (‒2; ‒3) là một nghiệm của phương trình (1). Do đó phát biểu c) là sai.

Vậy phát biểu b) là đúng, phát biểu a), c) là sai.

Bài 11 trang 14 SBT Toán 9 Tập 1: a) Chứng tỏ rằng các cặp số (‒5; 2), (0; 2), (2; 2) đều là nghiệm của phương trình 0x ‒ 2y = ‒4.

b) Trong các cặp số (7; 1),(1; 7),(1; 0),(0; 1), $\left(1;-\frac{5}{2}\right),$ cho biết cặp số nào là nghiệm của phương trình 3x ‒ 0y = 3.

Lời giải:

a) Xét phương trình: 0x ‒ 2y = ‒ 4. (1)

Thay x = ‒5; y = 2 vào phương trình (1) ta có: 0.(‒5) ‒ 2.2 = ‒4;

Thay x = 0; y = 2 vào phương trình (1) ta có: 0.0 ‒ 2.2 = ‒4;

Thay x = 2; y = 2 vào phương trình (1) ta có: 0.2 ‒ 2.2 = ‒4.

Vậy các cặp số (‒5; 2), (0; 2), (2; 2) đều là nghiệm của phương trình 0x ‒ 2y = ‒4.

b) Xét phương trình: 3x ‒ 0y = 3. (2)

Thay x = 7; y = 1 vào phương trình (2) ta có: 3.7 ‒ 0.1 = 21 ≠ 3;

Thay x = 1; y = 7 vào phương trình (2) ta có: 3.1 ‒ 0.7 = 3;

Thay x = 1; y = 0 vào phương trình (2) ta có: 3.1 ‒ 0.0 = 3;

Thay x = 0; y = 1 vào phương trình (2) ta có: 3.0 ‒ 0.1 = 0 ≠ 3;

Thay x = 7; $y=-\frac{5}{2}$ vào phương trình (2) ta có: $3\cdot 7-0\cdot \left(-\frac{5}{2}\right)=21\ne 3.$

Vậy các cặp số (1; 7) và (1; 0) là nghiệm của phương trình 3x ‒ 0y = 3.

Bài 12 trang 14 SBT Toán 9 Tập 1: Ba bạn An, Bình, Chi cùng đi nhà sách. Cả ba bạn đã mua hết 279 000 đồng. Ba bạn đã mua 3 quyển truyện với giá 45 000 đồng/quyển và mua thêm bút bi, bút chì màu. Giá của bút bi và bút chì màu lần lượt là 3 600 đồng/chiếc và 5 000 đồng/chiếc. Gọi x và y lần lượt là số chiếc bút bi và bút chì màu mà ba bạn đã mua. Viết phương trình bậc nhất hai ẩn cho số tiền mà ba bạn đã dùng để mua bút bi, bút chì màu và chỉ ra một nghiệm của phương trình đó.

Lời giải:

Số tiền ba bạn dùng để mua bút bi là: 3 600x (đồng).

Số tiền ba bạn dùng để mua bút chì màu là: 5 000y (đồng).

Tổng số tiền ba bạn dùng để mua bút bi và bút chì màu là: 3 600x + 5 000y (đồng).

Số tiền ba bạn đã mua 3 quyển truyện là:

3 . 45 000 = 135 000 (đồng).

Số tiền còn lại dùng để mua bút bi xanh và bút chì màu là:

279 000 ‒ 135 000 = 144 000 (đồng).

Phương trình bậc nhất hai ẩn cho số tiền mà ba bạn đã dùng để mua bút bi, bút chì màu là:

3 600x + 5 000y = 144 000 hay 18x + 25y = 720.

Từ phương trình 18x + 25y = 720, ta suy ra $x=\frac{720-25y}{18}=40-\frac{25}{18}y.$

Chọn y = 18, ta có x = 40 – 25 = 15.

Vậy một nghiệm của phương trình là (15; 18).

Bài 13 trang 14 SBT Toán 9 Tập 1: Cô Hà sử dụng dịch vụ điện thoại di động với giá cước gọi nội mạng và gọi ngoại mạng lần lượt là 1 190 đồng/phút và 1 390 đồng/phút. Trong tháng 10, cô Hà đã sử dụng 500 phút gọi (cả nội mạng và ngoại mạng) với tiền cước là 635 000 đồng. Gọi x và y lần lượt là số phút gọi nội mạng và ngoại mạng trong tháng 10 của cô Hà.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (300; 200) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Tổng số phút gọi trong tháng 10 của cô Hà là: x + y (phút).

Theo bài, trong tháng 10, cô Hà đã sử dụng 500 phút gọi nên ta có phương trình:

x + y = 500.

Tiền cước gọi nội mạng trong tháng 10 của cô Hà là: 1 190x (đồng).

Tiền cước gọi ngoại mạng trong tháng 10 của cô Hà là: 1 390y (đồng).

Tổng số tiền cước gọi trong tháng 10 của cô Hà là: 1 190x + 1 390y (đồng).

Theo bài, trong tháng 10, cô Hà đã trả tiền cước là 635 000 đồng nên ta có phương trình:

1 190x + 1 390y = 635 000.

Ta có hệ hai phương trình bậc nhất hai ẩn x; y biểu thị mối quan hệ giữa các đại lượng là:

$\left\{\begin{array}{l}x+y=500\\ 1190x+1390y=635000\end{array}\right.$ hay $\left\{\begin{array}{l}x+y=500\\ 119x+139y=63500.\end{array}\right.$

b) Thay x = 300; y = 200 vào mỗi phương trình trong hệ ta có:

300 + 200 = 500;

119.300 + 139.200 = 63 500.

Suy ra cặp số (300; 200) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (300; 200) là nghiệm của hệ phương trình ở câu a.

Bài 14 trang 14 SBT Toán 9 Tập 1: Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6,8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50 000 đồng/mét.

a) Viết hệ hai phương trình bậc hai ẩn x; y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (13; 9,6) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Chu vi mảnh đất thứ nhất có dạng hình vuông là: 4x (m).

Chu vi mảnh đất thứ hai có dạng hình chữ nhật là: 2.(x + y) (m).

Theo bài, chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6,8 m nên ta có phương trình:

4x ‒ 2(x + y) = 6,8

4x – 2x – 2y = 6,8

2x – 2y = 6,8

x ‒ y = 3,4. (1)

Chiều dài của khu đất là: x + y (m).

Chi phí xây tường rào là: 50 000(x + y) (đồng).

Theo bài, chi phí xây tường rào là 1 130 000 đồng nên ta có phương trình:

50 000(x + y)  = 1 130 000 hay x + y = 22,6. (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}x-y=3,4\\ x+y=22,6.\end{array}\right.$

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x-y=3,4\\ x+y=22,6.\end{array}\right.$

b) Xét cặp số (13; 9,6), thay x = 13; y = 9,6 vào mỗi phương trình trong hệ ta có:

13 ‒ 9,6 = 3,4;

13 + 9,6 = 22,6.

Suy ra cặp số (13; 9,6) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (13; 9,6) có phải là nghiệm của hệ phương trình ở câu a.

Bài 15 trang 15 SBT Toán 9 Tập 1:

 Người ta muốn pha dung dịch HNO₃ 30% với dung dịch HNO₃ 55% để được dung dịch HNO₃ 50%. Gọi x và y lần lượt là số gam dung dịch HNO₃ 30% và HNO₃ 55% cần dùng để pha được 100 g dung dịch HNO₃ 50%.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (20; 80) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Khi pha x gam dung dịch HNO₃ 30% với y gam dung dịch HNO₃ 55%, ta được khối lượng dung dịch mới là: x + y (g).

Theo bài, sau khi pha ta được 100 g dung dịch HNO₃ 50% nên ta có phương trình:

x + y = 100. (1)

Khối lượng HNO₃ có trong x gam dung dịch HNO₃ 30% là: x.30% = 0,3x (g).

Khối lượng HNO₃ có trong y gam dung dịch HNO₃ 55% là: y.55% = 0,55y (g).

Tổng khối lượng HNO₃ có trong dung dịch đã pha là: 0,3x + 0,55y (g).

Theo bài, pha x gam dung dịch HNO₃ 30% với y gam dung dịch HNO₃ 55% được 100 g dung dịch HNO₃ 50% nên ta có phương trình:

$\frac{0,3x+0,55y}{100}\cdot 100\%=50\%$ hay 6x + 11y = 1 000. (2)

Từ (1) và (2) ta được hệ phương trình $\left\{\begin{array}{l}x+y=100\\ 6x+11y=1000.\end{array}\right.$

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x+y=100\\ 6x+11y=1000.\end{array}\right.$

b) Xét cặp số (20; 80), thay x = 20; y = 80 vào mỗi phương trình trong hệ ta có:

20 + 80 = 100;

6.20 + 11.80 = 1 000.

Suy ra cặp số (20; 80) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (20; 80) là nghiệm của hệ phương trình ở câu a.

Bài 16 trang 15 SBT Toán 9 Tập 1: Một ô tô đi từ địa điểm A đến địa điểm B với tốc độ x (km/h) thì đi hết y (giờ) với x > 10 và y > 0,5. Nếu tốc độ của ô tô giảm 10 km/h thì thời gian ô tô đi tăng 45 phút. Nếu tốc độ của ô tô tăng 10 km/h thì thời gian ô tô đi giảm 30 phút.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (50; 3) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Đổi 45 phút = $\frac{3}{4}$  giờ; 30 phút = $\frac{1}{2}$  (giờ).

Theo bài, ô tô đi hết quãng đường AB với tốc độ x (km/h) trong y (giờ) nên độ dài quãng đường AB là: xy (km).

⦁ Vận tốc của ô tô khi giảm 10 km/h là: x – 10 (km/h).

Thời gian ô tô đi hết quãng đường AB khi giảm vận tốc là:  $y+\frac{3}{4}$(giờ).

Khi đó, quãng đường ô tô di chuyển là: $\left(x-10\right)\left(y+\frac{3}{4}\right)$  (km).

Do quãng đường di chuyển là không đổi nên ta có phương trình:

$\left(x-10\right)\left(y+\frac{3}{4}\right)=xy.$

$xy+\frac{3}{4}x-10y-\frac{30}{4}=xy$

$xy+\frac{3}{4}x-10y-xy=\frac{30}{4}$

$\frac{3}{4}x-10y=\frac{30}{4}$

3x ‒ 40y = 30. (1)

⦁ Vận tốc của ô tô khi tăng 10 km/h là: x + 10 (km/h).

Thời gian ô tô đi hết quãng đường AB khi tăng vận tốc là: y - $\frac{1}{2}$  (giờ).

Khi đó, quãng đường ô tô di chuyển là: $\left(x+10\right)\left(y-\frac{1}{2}\right)$  (km).

Do quãng đường di chuyển là không đổi nên ta có phương trình:

$\left(x+10\right)\left(y-\frac{1}{2}\right)=xy$

$xy-\frac{x}{2}+10y-5=xy$

$xy-\frac{x}{2}+10y-xy=5$

$-\frac{x}{2}+10y=5$

- x + 20y = 10. (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}3x-40y=30\\ -x+20y=10.\end{array}\right.$

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}3x-40y=30\\ -x+20y=10.\end{array}\right.$

b) Xét cặp số (50; 3), thay x = 50; y = 3 vào mỗi phương trình trong hệ ta có:

3.50 ‒ 40.3 = 30;

‒50 + 20.3 = 10.

Suy ra cặp số (50; 3) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (50; 3) là nghiệm của hệ phương trình ở câu a.

Xem thêm các bài giải Sách bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Bài tập cuối chương 1

Bài 1: Bất đẳng thức

Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn

Ví dụ: $2x+3y=4$, $0x+2y=3$, $x+0y=2$ là các phương trình bậc nhất hai ẩn.

Nghiệm của phương trình bậc nhất hai ẩn

Ví dụ: Cặp số $(-1;2)$ là nghiệm của phương trình $2x+3y=4$ vì $2.\left(-1\right)+3.2=-2+6=4$.

Cặp số $(1;2)$ không là nghiệm của phương trình $2x+3y=4$ vì

$2.1+3.2=2+6=8\ne 4$.

Chú ý:

Ta cũng áp dụng được quy tắc chuyển vế, quy tắc nhân đã biết ở phương trình bậc nhất một ẩn để biến đổi phương trình bậc nhất hai ẩn.

Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm của phương trình $ax+by=c$ được biểu diễn bởi một điểm. Nghiệm $\left(x_0;y_0\right)$ được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$.

- Mỗi nghiệm của phương trình $ax+0y=c\left(a\ne 0\right)$ được biểu diễn bởi điểm có tọa độ $\left(\frac{c}{a};y_0\right)$ $\left(y_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_1:x=\frac{c}{a}$. Đường thẳng $d_1$ là đường thẳng đi qua điểm $\frac{c}{a}$ trên trục Ox và vuông góc với trục Ox.

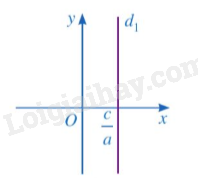
- Mỗi nghiệm của phương trình $0x+by=c\left(b\ne 0\right)$ được biểu diễn bởi một điểm có tọa độ $\left(x_0;\frac{c}{b}\right)\left(x_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_2:y=\frac{c}{b}$. Đường thẳng $d_2$ là đường thẳng đi qua điểm $\frac{c}{b}$ trên trục Oy và vuông góc với trục Oy.

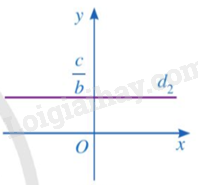
- Mỗi nghiệm của phương trình $ax+by=c\left(a\ne 0,b\ne 0\right)$ được biểu diễn bởi một điểm nằm trên đường thẳng $d_3:y=-\frac{a}{b}x+\frac{c}{b}$.

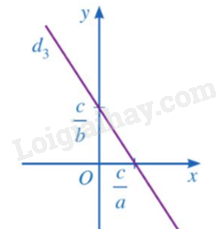
Ví dụ:

Nghiệm của phương trình $-3x+y=2$ được biểu diễn bởi đường thẳng d: $y=3x+2$.

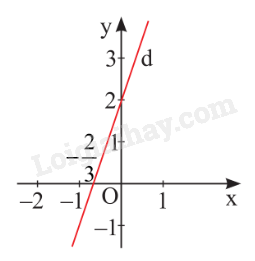
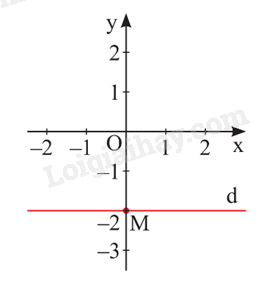
Nghiệm của phương trình $0x+y=-2$ được biểu diễn bởi đường thẳng d: $y=-2$ vuông góc với Oy tại điểm $M\left(0;-2\right)$.

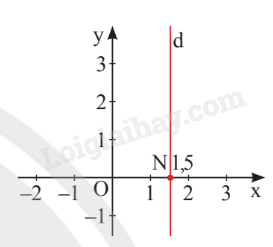
Nghiệm của phương trình $2x+0y=3$ được biểu diễn bởi đường thẳng d: $x=1,5$ vuông góc với Ox tại điểm $N\left(1,5;0\right)$.

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, $\{\begin{array}{l}3x=1\\ x-y=3\end{array}$, $\{\begin{array}{l}4x-y=3\\ 3y=6\end{array}$ là các hệ phương trình bậc nhất hai ẩn.

Nghiệm của hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, vì:

$2x-y=2.1-2=0$ nên (1; 2) là nghiệm của phương trình thứ nhất.

$x+y=1+2=3$ nên (1; 2) là nghiệm của phương trình thứ hai.