Với giải sách bài tập Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực

Giải SBT Toán 7 trang 40 Tập 1

Bài 1 trang 40 Sách bài tập Toán 7 Tập 1: Hãy thay dấu $\boxed{?}$ bằng kí hiệu ∈ hoặc ∉ để có phát biểu đúng.

3,9 $\boxed{?}$ ℤ;

29% $\boxed{?}$ ℚ;

$\sqrt{7}$ $\boxed{?}$ ℚ;

$-\frac{4}{99}$ $\boxed{?}$ ℚ;

$\sqrt{3}$ $\boxed{?}$ ?;

$\sqrt{5}$ $\boxed{?}$ ℝ;

π $\boxed{?}$ ?;

Lời giải

Ta có 3,9 là số hữu tỉ không phải là số nguyên nên 3,9 ∉ ℤ. Khi đó ta điền: 3,9 $\boxed{\notin }$ ℤ.

Ta có 29% = $\frac{29}{100}$ (trong đó 29, 100 ∈ ℤ và 100 ≠ 0) nên 29% ∈ ℚ. Khi đó ta điền: 29% $\boxed{\in }$ ℚ.

Ta có $\sqrt{7}\approx 2,\mathrm{645751311...}$ là số thập phân vô hạn không tuần hoàn nên $\sqrt{7}$ là số vô tỉ mà số vô tỉ không là số hữu tỉ do đó$\sqrt{7}$ ∉ ℚ. Khi đó ta điền$\sqrt{7}$ $\boxed{\notin }$ ℚ.

Ta có: $-\frac{4}{99}$ (trong đó 4; 99 ∈ ℤ và 99 ≠ 0) nên $-\frac{4}{99}$∈ ℚ. Khi đó ta điền $-\frac{4}{99}$ $\boxed{\in }$ ℚ.

Ta có: $\sqrt{3}\approx 1,\mathrm{732050808...}$ là số thập phân vô hạn không tuần hoàn nên $\sqrt{3}$ ∈ ?. Khi đó ta điền:$\sqrt{3}$ $\boxed{\in }$ ?.

Ta có:$\sqrt{5}\approx 2,\mathrm{236067977...}$ là số thập phân vô hạn không tuần hoàn nên $\sqrt{5}$ là số vô tỉ, mà số thực bao gồm số hữu tỉ và số vô tỉ. Khi đó ta điền $\sqrt{5}$$\boxed{\in }$ ℝ.

Ta có π ≈ 3,141592654... là số thập phân vô hạn không tuần hoàn nên π là số vô tỉ. Khi đó ta điền π $\boxed{\in }$ ?.

Bài 2 trang 40 Sách bài tập Toán 7 Tập 1: Sắp xếp theo thứ tự từ nhỏ đến lớn các số thực sau: $\frac{4}{5};$ 0,(8); $\sqrt{3}$; 1,74; – π; – 3,142; 2.

Lời giải

Ta có: $\frac{4}{5}=0,8$; – π = – 3,141592654...; $\sqrt{3}=1,\mathrm{732050808...}$

Vì 3,141592654... < 3,142 nên – 3,141592654... > – 3,142 hay – 3,142 < – π. (1)

Ta lại có 0,8 < 0,(8) < 1,732050808... < 1,74 < 2 nên $\frac{4}{5}$ < 0,(8) <$\sqrt{3}$ < 1,74 < 2. (2)

Từ (1) và (2) suy ra  – 3,142 < – π < $\frac{4}{5}$ < 0,(8) <$\sqrt{3}$ < 1,74 < 2.

Vậy theo thứ tự từ nhỏ đến lớn ta có dãy: – 3,142; – π; $\frac{4}{5}$; 0,(8);$\sqrt{3}$; 1,74; 2.

Bài 3 trang 40, 41 Sách bài tập Toán 7 Tập 1: Hãy cho biết tính đúng, sai của các khẳng định sau:

a) $\sqrt{4};\sqrt{9};\sqrt{25}$là các số vô tỉ;

b) Số vô tỉ không phải là số thực;

c) $-\frac{1}{2};\frac{2}{3};-0,45$ là các số hữu tỉ;

d) Số 0 là số vô tỉ;

e) 0,1; 0; 9; 99% là các số hữu tỉ.

Lời giải

a) Ta có:

2² = 4 (2 > 0) nên $\sqrt{4}$ = 2 là số hữu tỉ, mà số hữu tỉ không là số vô tỉ;

3² = 9 (3 > 0) nên $\sqrt{9}$= 3 là số hữu tỉ, mà số hữu tỉ không là số vô tỉ;

5² = 25 (5 > 0) nên $\sqrt{25}$ = 5 là số hữu tỉ, mà số hữu tỉ không là số vô tỉ.

Suy ra $\sqrt{4};\sqrt{9};\sqrt{25}$là các số hữu tỉ. Do đó a) sai.

b) Số thực bao gồm số hữu tỉ và số vô tỉ nên số vô tỉ là số thực. Do đó b) sai.

c) Ta có:

$-\frac{1}{2}$ (trong đó -1; 2 ∈ ℤ, 2 ≠ 0) là số hữu tỉ;

$\frac{2}{3}$ (trong đó 3; 2 ∈ ℤ, 3 ≠ 0) là số hữu tỉ;

$-0,45=-\frac{45}{100}$ (trong đó -45; 100 ∈ ℤ, 100 ≠ 0) là số hữu tỉ;

Suy ra$-\frac{1}{2};\frac{2}{3};-0,45$ là các số hữu tỉ. Do đó c) đúng.

d) Số 0 là số hữu tỉ và không là số vô tỉ. Do đó d) sai.

e) Ta có: 0,1 = $\frac{1}{10}$ (trong đó 1; 10 ∈ ℤ, 10 ≠ 0) là số hữu tỉ;

0 = $\frac{0}{1}$ (trong đó 0; 1 ∈ ℤ, 10 ≠ 0) là số hữu tỉ;

9 = $\frac{9}{1}$(trong đó 9; 1 ∈ ℤ, 1 ≠ 0) là số hữu tỉ;

99% =  $\frac{99}{100}$(trong đó 9; 100 ∈ ℤ, 100 ≠ 0) là số hữu tỉ.

Suy ra 0,1; 0; 9; 99% là các số hữu tỉ. Do đó e) đúng.

Giải SBT Toán 7 trang 41 Tập 1

Bài 4 trang 41 Sách bài tập Toán 7 Tập 1: Hãy thay dấu ? bằng các số thích hợp:

a) 9,289 > 9,2$\boxed{?}$79;

b) -0,3489 > -0,34$\boxed{?}$8.

Lời giải

a) Hai số thập phân này có cùng phần nguyên, từ trái qua phải hai chữ số thập phân thứ nhất bằng nhau.

Vì 9 > 7 nên để 9,289 > 9,2$\boxed{?}$79 thì chữ số cần điền có thể là: 0; 1; 2; 3; 4; 5; 6; 7; 8.

Vậy các số thích hợp để thay cho dấu ? là 0; 1; 2; 3; 4; 5; 6; 7; 8.

b) Hai số thập phân này có cùng phần nguyên, từ trái qua phải hai chữ số thập phân thứ nhất, thứ hai bằng nhau.

Vì 9 > 8 nên để -0,3489 > -0,34$\boxed{?}$8 thì chữ số cần điền chỉ có thể là: 9.

Vậy các số thích hợp để thay cho dấu ? là 9.

Bài 5 trang 41 Sách bài tập Toán 7 Tập 1: Tìm số đối của các số sau: π; 25%; – 5; $-\sqrt{11}$; $-\frac{3}{5}$.

Lời giải

Số đối của π là – π;

Số đối của 25% là – 25%;

Số đối của – 5 là – (– 5);

Số đối của $-\sqrt{11}$ là $-\left(-\sqrt{11}\right)=\sqrt{11}$;

Số đối của $-\frac{3}{5}$ là $-\left(-\frac{3}{5}\right)=\frac{3}{5}$.

Bài 6 trang 41 Sách bài tập Toán 7 Tập 1: Tìm giá trị tuyệt đối của các số sau:

$\sqrt{9};-23;-90\%;\frac{5}{4};-\pi$.

Lời giải

Ta có: 

Vì $\sqrt{9}>0$ nên $\left|\sqrt{9}\right|=\left|\sqrt{3^2}\right|=3$;

Vì – 23 < 0 nên |– 23| =  – ( – 23) = 23;

Vì  – 90% < 0 nên | – 90%| = 0 – (– 90%) = 90%;

Vì $\frac{5}{4}>0$ nên $\left|\frac{5}{4}\right|=\frac{5}{4};$

Vì  – π < 0 nên |– π| = – (– π) =  π.

Vậy giá trị tuyệt đối của $\sqrt{9};-23;-90\%;\frac{5}{4};-\pi$ lần lượt là $3;23;90\%;\frac{5}{4};\pi .$

Bài 7 trang 41 Sách bài tập Toán 7 Tập 1: Sắp xếp theo thứ tự từ nhỏ đến lớn giá trị tuyệt đối của các số sau: – 1,99; 1,9; $-\sqrt{3}$; $1\frac{1}{9}$.

Lời giải

+) Ta có:

Vì – 1,99 < 0 nên |– 1,99| = 0 – ( – 1,99) = 1,99;

Vì 1,9 > 0 nên |1,9| = 1,9;

Vì $-\sqrt{3}<0$nên $\left|-\sqrt{3}\right|=-\left(-\sqrt{3}\right)=\sqrt{3}$;

Vì $1\frac{1}{9}$ > 0 nên $\left|1\frac{1}{9}\right|=1\frac{1}{9}$.

+) So sánh giá trị tuyệt đối

Vì 0 < 9 nên 1,9 < 1,99 (1)

Ta lại có: $\sqrt{3}=1,\mathrm{732050808...}$; $1\frac{1}{9}=1+\frac{1}{9}=1+0,\left(1\right)=1,\left(1\right)$

Vì 1 < 7 < 9 nên 1,(1) < 1,732050805... < 1,9 (2)

Từ (1) và (2) suy ra 1,(1) < 1,732050805... < 1,9 < 1,99 hay $1\frac{1}{9}$; $\sqrt{3}$; 1,9; 1,99.

Vậy theo thứ tự từ nhỏ đến lớn giá trị tuyệt đối của các số sau: – 1,99; 1,9; $-\sqrt{3}$; $1\frac{1}{9}$ là: $1\frac{1}{9}$; $\sqrt{3}$; 1,9; 1,99.

Bài 8 trang 41 Sách bài tập Toán 7 Tập 1: Tìm giá trị của x, biết rằng: 2|x| = $\sqrt{12}$.

Lời giải

2|x| = $\sqrt{12}$

|x| = $\sqrt{12}$:2

|x| = $\frac{\sqrt{12}}{2}$

x = $\frac{\sqrt{12}}{2}$ hoặc x = $-\frac{\sqrt{12}}{2}$.

Vậy x = $\frac{\sqrt{12}}{2}$ hoặc x = $-\frac{\sqrt{12}}{2}$.

Bài 9 trang 41 Sách bài tập Toán 7 Tập 1: Tìm giá trị của y, biết rằng |2y – 5| = 0.

Lời giải

|2y – 5| = 0

2y – 5 = 0

2y = 5

y = 5 : 2

y = $\frac{5}{2}$

Vậy y = $\frac{5}{2}$.

Bài 10 trang 41 Sách bài tập Toán 7 Tập 1: Rút gọn biểu thức: M = $\sqrt{a^2}$.

Lời giải

TH1. Nếu a < 0 thì – a > 0 ta có (-a)² = a² nên $\sqrt{a^2}=-a$.

TH2. Nếu a ≥ 0, ta có $\sqrt{a^2}=a$.

Vậy M = $\sqrt{a^2}=\left|a\right|=\left\{\begin{array}{l}-akhia<0\\ akhia>0\end{array}\right.$.

Bài 11 trang 41 Sách bài tập Toán 7 Tập 1: Cho một hình vuông có diện tích 5m². Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361 m.

Lời giải

Vì diện tích hình vuông bằng bình phương độ dài cạnh nên độ dài cạnh bằng căn bậc hai số học của diện tích.

Độ dài a của cạnh hình vuông là:

$a=\sqrt{5}=2,\mathrm{236067977...}$ (m)

Ta có: $\sqrt{5}=2,\mathrm{236067977...}$

Vì 2 < 3 nên 2,236067977... < 2,361 hay $\sqrt{5}$< 2,361.

Vậy độ dài cạnh a của hình vuông là $\sqrt{5}$ và a < b.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 2: Số thực. Giá trị tuyệt đối của một số thực

Bài 3: Làm tròn số và ước lượng kết quả

Bài tập cuối chương 2

Bài 1: Hình hộp chữ nhật – hình lập phương

Lý thuyết Số thực. Giá trị tuyệt đối của một số thực

1. Số thực và tập hợp các số thực

– Ta gọi chung số hữu tỉ và số vô tỉ là số thực.

– Tập hợp số thực được kí hiệu ℝ.

Cách viết x ∈ ℝ cho ta biết x là một số thực.

– Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau:

+ Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu số đó là số hữu tỉ.

+ Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.

Ví dụ: Ta có các số 5; –3 ; 0,14 ; $-\frac{8}{7}$ ; $3\frac{1}{8}$ ; $\sqrt{11}$ ; π ; ….là các số thực.

Ta viết 5 ∈ ℝ ; –3 ∈ ℝ ; 0,14 ∈ ℝ ; $-\frac{8}{7}$ ∈ ℝ ; $3\frac{1}{8}$ ∈ ℝ; $\sqrt{11}$ ∈ ℝ ; π ∈ ℝ ; …

Chú ý: Trong các tập hợp đã học, tập hợp số thực là “rộng lớn” nhất bao gồm tất cả các số tự nhiên, số nguyên, số hữu tỉ và cả số vô tỉ.

– Trong tập hợp các số thực, ta cũng có các phép tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.

2. Thứ tự trong tập hợp các số thực

– Các số thập phân hữu hạn hoặc vô hạn đều có thể so sánh tương tự như so sánh hai số thập phân hữu hạn, đó là so sánh phần số nguyên, rồi đến phần thập phân thứ nhất, phần thập phân thứ hai, …

– Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng.

Do vậy: Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.

Chú ý: Với hai số thực dương a và b, ta có:

Nếu a > b thì $\sqrt{a}>\sqrt{b}$.

Ví dụ: So sánh hai số thực:

a) 5,(56) và 5,566;

b) $\sqrt{3}$ và 1,733;

c) –1,024 và –1,025;

d) $\sqrt{8}$ và 3.

Hướng dẫn giải

a) Số 5,(56) = 5,565656… < 5,566 (do phần thập phân thứ ba của hai số ta thấy 5 < 6).

Vậy 5,(56) < 5,566.

b) Ta có: $\sqrt{3}$ = 1,73205… < 1,733 (do phần thập phân thứ ba của hai số ta thấy 2 < 3).

Vậy $\sqrt{3}$ < 1,733.

c) Ta có: 1,024 < 1,025 (do phần thập phân thứ ba của hai số ta thấy 4 < 5)

Suy ra: –1,024 > –1,025.

Vậy –1,024 > –1,025.

d) Do 8 < 9 nên ta có $\sqrt{8}<\sqrt{9}$, tức là $\sqrt{8}$ < 3 (vì $\sqrt{9}$ = 3).

Vậy $\sqrt{8}$ < 3.

3. Trục số thực

Ta đã biết một hình vuông có cạnh bằng 1 có độ dài đường chéo là $\sqrt{2}.$

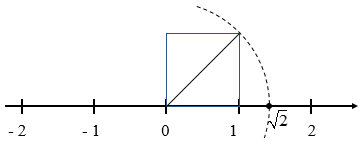
– Trên trục số ta biểu diễn được số vô tỉ $\sqrt{2}.$. Vì vậy, không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ, nghĩa là các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

Người ta chứng minh được rằng:

+  Mỗi số thực được biểu diễn bởi một điểm trên trục số

+ Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

Vì vậy, ta gọi trục số là trục số thực.

Chú ý:

– Điểm biểu diễn số thực x trên trục số được gọi là điểm x. 

– Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ: Ta có: $\sqrt{2}.$ = 1,414213562… < 1,5.

Vậy điểm $\sqrt{2}.$ nằm bên trái điểm 1,5 trên trục số nằm ngang.

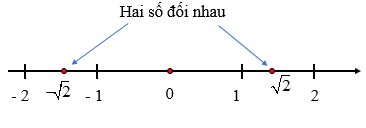
4. Số đối của một số thực

– Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số thực x kí hiệu là –x.

– Ta có x + (– x) = 0.

Ví dụ:  Số đối của số $\sqrt{2}$ là $-\sqrt{2}$, số đối của $-\sqrt{2}$ là $\sqrt{2}$.

5. Giá trị tuyệt đối của một số thực

Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.

Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.

Nhận xét: Ta có$\left|x\right|\text{ = }\left\{\begin{array}{c}x\text{ khi x > 0}\\ -x\text{ \hspace{0.17em}khi x < 0}\\ 0\text{ \hspace{0.17em}khi x =\hspace{0.17em} 0}\end{array}\right.$

Vậy giá trị tuyệt đối của một số thực x luôn là số không âm:

|x| ≥ 0 với mọi số thực x.

Ví dụ:

a)

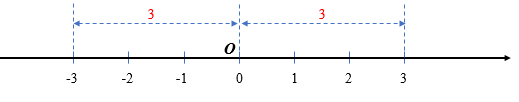
– Khoảng cách từ điểm –3 đến điểm 0 là 3 nên |–3| = 3.

– Khoảng cách từ điểm 3 đến gốc 0 là 3 nên |3| = 3.

b) Vì –2 < 0 nên |–2| = –(–2) = 2.