Sách bài tập Toán 8 Bài 8 (Cánh diều): Trường hợp đồng dạng thứ ba của tam giác

Admin Vietjack Ngày: 23-09-2024 Lớp 8

1.6 K

Với giải sách bài tập Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Giải SBT Toán 8 trang 78

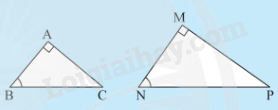
Bài 44 trang 78 SBT Toán 8 Tập 2: Quan sát Hình 43 và chỉ ra hai cặp tam giác đồng dạng:

Quan sát Hình 43 và chỉ ra hai cặp tam giác đồng dạng

Lời giải:

• Tam giác DEF có ED = FD nên tam giác DEF cân tại D.

Suy ra $\hat{EFD} = \hat{F E D} = 69 ° .$

Ta có: $\hat{EFD} + \hat{F E D} + \hat{E D F} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{E D F} = 180 ° - \hat{EFD} - \hat{F E D}$ = $180 ° - 69 ° - 69 ° = 42 ° .$

Xét ∆ABC và ∆DEF có:

$\hat{B A C} = \hat{E D F} = 42 °;$

$\frac{A B}{D E} = \frac{A C}{D F}$ (do AB = AC, ED = FD)

Suy ra ∆ABC ᔕ ∆DEF (c.g.c).

• Xét ∆ MNP có: $\hat{M} + \hat{N} + \hat{P} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{P} = 180 ° - \hat{M} - \hat{N}$ = $180 ° - 72 ° - 63 ° = 45 ° .$

Xét ∆MNP và ∆HIK có:

$\hat{M} = \hat{H} = 72 °; \hat{P} = \hat{K} = 45 °$

Suy ra ∆MNP ᔕ ∆HIK (g.g).

Bài 45 trang 78 SBT Toán 8 Tập 2: Cho hình thang ABCD có AB // CD, AB = 4 cm, DB = 6 cm và $\hat{D A B} = \hat{D B C} .$ Tính độ dài CD.

Lời giải:

Cho hình thang ABCD có AB // CD, AB = 4 cm, DB = 6 cm

Ta có: AB // CD nên $\hat{A B D} = \hat{B D C}$ (hai góc so le trong).

Xét ∆ABD và ∆BDC có:

$\hat{D A B} = \hat{D B C};$

$\hat{A B D} = \hat{B D C}$

Suy ra ∆ABD ᔕ ∆BDC (g.g).

Do đó $\frac{A B}{B D} = \frac{B D}{D C}$ (tỉ số đồng dạng)

Nên $C D = \frac{B D^{2}}{A B} = \frac{6^{2}}{4} = 9$ (cm).

Vậy CD = 9 cm.

Bài 46 trang 78 SBT Toán 8 Tập 2: Bác An cần đo khoảng cách AC, với A, C nằm ở hai bên bờ của một hồ nước (Hình 44a). Bác An đã tiến hành đo như sau:

• Chọn điểm B trên bờ (có điểm C) sao cho BC = 20 m;

• Dùng thước đo góc, đo được các góc $\hat{A B C} = 32 °, \hat{A C B} = 77 ° .$

Chứng minh rằng: Nếu thực hiện vẽ trên giấy một tam giác DEF sao cho EF = 10 (cm), $\hat{D E F} = 32 °$ , $\hat{D F E} = 77 °$ (Hình 44b); Đo dộ dài đoạn DF và già sử DF = a (cm) thì độ dài AC mà bác An cần đo là 2a (m).

Bác An cần đo khoảng cách AC, với A, C nằm ở hai bên bờ của một hồ nước (Hình 44a)

Lời giải:

Đổi 20 m = 2 000 cm.

Xét ∆ABC và ∆DEF có:

$\hat{A B C} = \hat{D E F} = 32 °$ , $\hat{A C B} = \hat{D F E} = 77 °$

Suy ra ∆ABC ᔕ ∆DEF (g.g).

Do đó $\frac{B C}{E F} = \frac{A C}{D F}$ (tỉ số đồng dạng)

Hay $\frac{2 000}{10} = \frac{A C}{a}$ nên AC = 200a (cm) = 2a (m).

Giải SBT Toán 8 trang 79

Bài 47 trang 79 SBT Toán 8 Tập 2: Cho tam giác ABC. Lấy E, F, P lần lượt thuộc AB, AC, BC sao cho tứ giác BEFP là hình bình hành (Hình 45). Biết diện tích tam giác AEF và CFP lần lượt bằng 16 cm² và 25 cm².

a) Hãy chỉ ra ba cặp tam giác đồng dạng.

b) Tính diện tích tam giác ABC.

Cho tam giác ABC. Lấy E, F, P lần lượt thuộc AB, AC, BC sao cho tứ giác BEFP

Lời giải:

a) Do BEFP là hình bình hành nên EF // BP, FP // BE.

Mà E ∈ AB, P ∈ BC nên EF // BC, FP // AB.

Ta có:

• EF // BC nên ∆AEF ᔕ ∆ABC;

• FP // AB nên ∆FPC ᔕ ∆ABC;

• Do ∆AEF ᔕ ∆ABC và ∆FPC ᔕ ∆ABC nên ∆AEF ᔕ ∆FPC.

b) Ta dễ dàng chứng minh được, ∆AEF ᔕ ∆ABC thì $\frac{S_{Δ A E F}}{S_{Δ A B C}} = {(\frac{E F}{B C})}^{2}$

Suy ra $\sqrt{\frac{S_{Δ A E F}}{S_{Δ A B C}}} = \frac{E F}{B C}$ (1).

Ta cũng có ∆FPC ᔕ ∆ABC nên $\frac{S_{Δ F P C}}{S_{Δ A B C}} = {(\frac{C P}{B C})}^{2}$

Suy ra $\sqrt{\frac{S_{Δ F P C}}{S_{Δ ABC}}} = \frac{C P}{B C}$ (2).

Từ (1) và (2) ta có:

$\sqrt{\frac{S_{Δ A E F}}{S_{Δ A B C}}} + \sqrt{\frac{S_{Δ F P C}}{S_{Δ A B C}}}$ = $\frac{E F}{B C} + \frac{C P}{B C} = \frac{B P}{B C} + \frac{C P}{B C} = \frac{B C}{B C} = 1$ (do BEFP là hình bình hành nên EF = BP)

Cho tam giác ABC. Lấy E, F, P lần lượt thuộc AB, AC, BC sao cho tứ giác BEFP

Vậy S_ABC = 81 m².

Bài 48 trang 79 SBT Toán 8 Tập 2: Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB), CF vuông góc với AD (F thuộc đường thẳng AD). Chứng minh: AB.AE + AD.AF = AC².

Lời giải:

Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB)

Gọi H, K lần lượt là hình chiếu của D, B trên đường thẳng AC.

Xét ∆AHD và ∆AFC có:

$\hat{A H D} = \hat{A F C} = 90 °$ ; $\hat{F A C}$ là góc chung

Suy ra ∆AHD ᔕ ∆AFC (g.g).

Do đó $\frac{A D}{A C} = \frac{A H}{A F}$ (tỉ số đồng dạng) hay AD.AF = AC.AH (1).

Xét ∆AKB và ∆AEC có:

$\hat{AK B} = \hat{A E C} = 90 °$ ; $\hat{E A C}$ là góc chung

Suy ra ∆AKB ᔕ ∆AEC (g.g).

Suy ra $\frac{A B}{A C} = \frac{A K}{A E}$ (tỉ số đồng dạng) hay AB.AE = AC.AK (2).

Do ABCD là hình bình hành nên AB = CD, AB // CD.

Suy ra $\hat{B A K} = \hat{D C H}$ (2 góc ở vị trí so le trong)

Xét ∆ABK và ∆CDH có:

AB = CD, $\hat{B A K} = \hat{D C H}$

Suy ra ∆ABK = ∆CDH (cạnh huyền – góc nhọn)

Do đó AK = HC (hai cạnh tương ứng).

Cộng (1) và (2) theo vế ta được:

AD.AF + AB.AE = AC.(AH + AK)

= AC.(AH + HC) (do AK = HC)

= AC.AC = AC².

Vậy AB.AE + AD.AF = AC².

Bài 49 trang 79 SBT Toán 8 Tập 2: Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC, H trên cạnh CD sao cho $\hat{G O H} = 45 ° .$ Gọi M là trung điểm của AB. Chứng minh:

a) ∆HOD ᔕ ∆OGB;

b) MG // AH.

Lời giải:

Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC

a) Do ABCD là hình vuông nên đường chéo là tia phân giác của mỗi góc.

Suy ra $\hat{C D B} = \hat{C B D} = 45 ° .$

Mặt khác:

$\hat{D O H} + \hat{B O G} = 180 ° - \hat{G O H} = 180 ° - 45 ° = 135 °;$

$\hat{B O G} + \hat{B G O} = 180 ° - \hat{O B G} = 180 ° - 45 ° = 135 ° .$

Suy ra $\hat{D O H} = \hat{B G O} .$

Xét ∆HOD và ∆OGB có:

$\hat{H D O} = \hat{O B G} = 45 °$ ; $\hat{D O H} = \hat{B G O}$

Suy ra ∆HOD ᔕ ∆OGB (g.g).

b) Theo câu a, ta có ∆HOD ᔕ ∆OGB, suy ra $\frac{H D}{O B} = \frac{O D}{G B}$ (tỉ số đồng dạng)

Do đó HD.GB = OB.OD.

Đặt MB = a, khi đó AD = 2a (do M là trung điểm của AB, AB = AD)

Xét ∆ABD vuông tại A, theo định lí Pythagore ta có: BD² = AB² + AD².

Do đó $B D = \sqrt{A B^{2} + A D^{2}}$ = $\sqrt{{(2 a)}^{2} + {(2 a)}^{2}} = \sqrt{8 a^{2}} = 2 a \sqrt{2} .$

Suy ra $O B = O D = a \sqrt{2} .$

Khi đó $H D . G B = O B . O D$ = $a \sqrt{2} \cdot a \sqrt{2} = 2 a^{2}$ = $2 a \cdot a = A D \cdot B M$

Vì HD.GB = AD.BM nên $\frac{H D}{B M} = \frac{A D}{B G}$

Xét ∆DHA và ∆BMG có:

$\hat{H D A} = \hat{M B G} = 90 °$ và $\frac{H D}{B M} = \frac{A D}{B G}$

Suy ra ∆DHA ᔕ ∆BMG (c.g.c).

Do đó $\hat{A H D} = \hat{M_{1}}$ (hai góc tương ứng)

Mà $\hat{A H D} = \hat{B A H}$ (hai góc so le trong do AB // CD).

Suy ra $\hat{M_{1}} = \hat{B A H}$

Mà $\hat{M_{1}}$ và $\hat{B A H}$ ở vị trí đồng vị nên MG // AH.

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài tập cuối chương 8

Lý thuyết Trường hợp đồng dạng thứ ba của tam giác

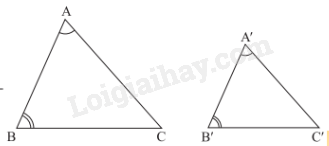
1. Trường hợp đồng dạng thứ ba (góc – góc)

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Lý thuyết Trường hợp đồng dạng thứ ba của tam giác (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

$\begin{array}{l} Δ A B C, Δ A^{'} B^{'} C^{'}, \hat{A^{'}} = \hat{A}, \hat{B^{'}} = \hat{B} \\ \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C \end{array}$