Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Trường hợp đồng dạng thứ ba của tam giác được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Trường hợp đồng dạng thứ ba của tam giác. Mời các bạn đón xem:
Bài tập Toán 8 Trường hợp đồng dạng thứ ba của tam giác
A. Bài tập Trường hợp đồng dạng thứ ba của tam giác
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
Hướng dẫn giải:
Đáp án : C
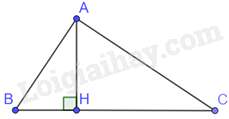
Tam giác ACH và tam giác CBA có:
Do đó,
Bài 2: Cho hình vẽ:
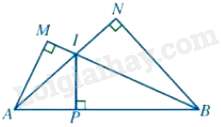
Chọn đáp án đúng
Hướng dẫn giải:
Đáp án : B
Tam giác ABN và tam giác AIP có:
Do đó,
Tam giác AMB và tam giác IPB có:
Do đó,
Vậy
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
Hướng dẫn giải:
Đáp án : A
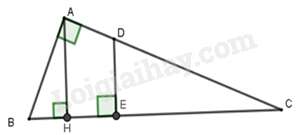
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Tam giác AHC và tam giác ABC có: Do đó,
Ta có: ,
Từ (1) và (2) ta có:
Tam giác DEC và tam giác AHC có:
Từ (3) và (4) ta có:
Bài 4: Cho hình vẽ:
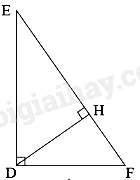
Khẳng định nào sau đây là đúng?
Hướng dẫn giải:
Đáp án : B
Ta có:
Tam giác EDH và tam giác DFH có:
Do đó, nên
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
Hướng dẫn giải:
Đáp án : A
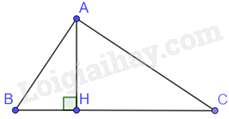
Tam giác ACH và tam giác CBA có:
Do đó,
B. Lý thuyết Trường hợp đồng dạng thứ ba của tam giác
1. Trường hợp đồng dạng thứ ba (góc – góc)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
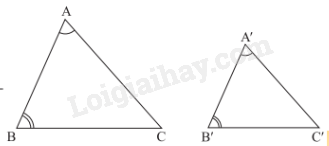
2. Trường hợp đồng dạng góc nhọn của tam giác vuông
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
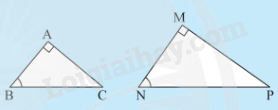
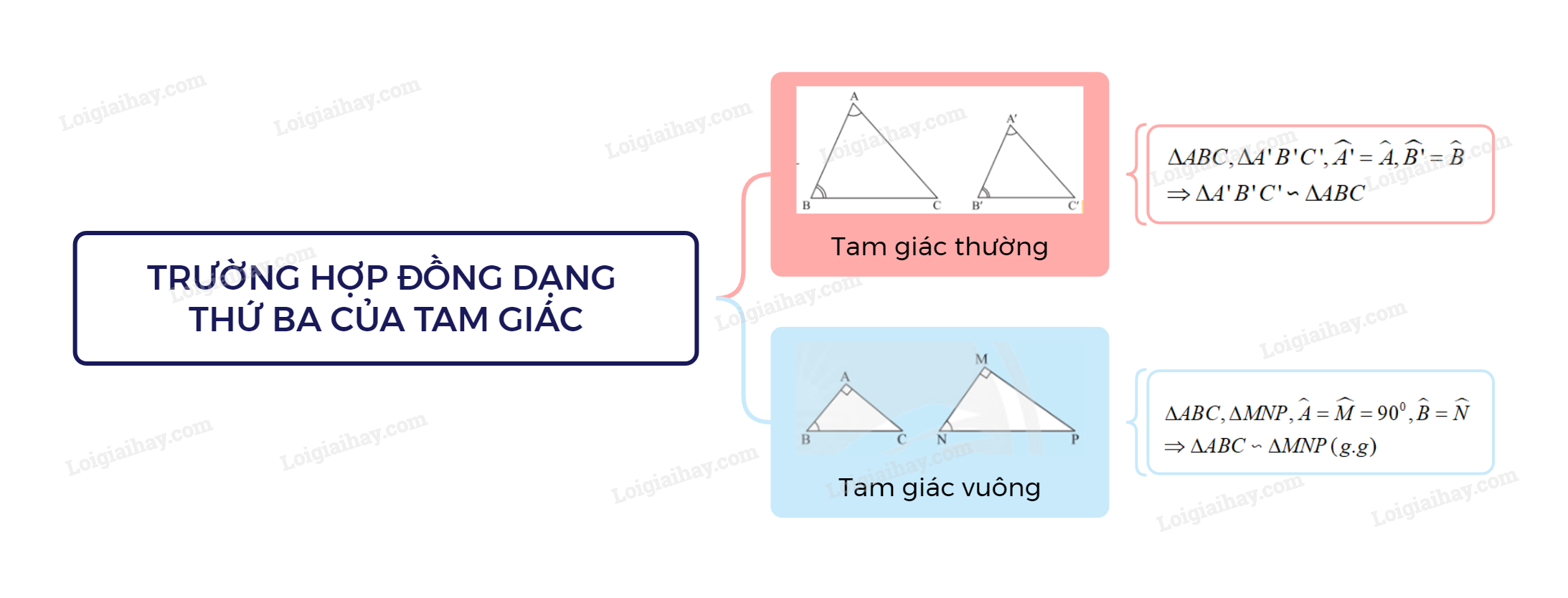
Sơ đồ tư duy Trường hợp đồng dạng thứ ba của tam giác