Với giải sách bài tập Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Lời giải:
Ta có:
Do đó:
Lời giải:
Do ∆MNP ᔕ ∆ABC nên (tỉ số đồng dạng)
Lại có chu vi của ∆ MNP là 46,5 cm nên MN + MP + NP = 46,5 (cm).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Suy ra: MN = 9.1,5 = 13,5 (cm); MP = 7.1,5 = 10,5 (cm); NP = 15.1,5 = 22,5 (cm).
Vậy MN = 13,5 cm; MP = 10,5 cm; NP = 22,5 cm.
Lời giải:
Do tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng là k nên
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Mà chu vi tam giác ABC là AB + BC + CA;
chu vi tam giác A’B’C’ là A’B’ + B’C’ + C’A’.
Vậy tỉ số chu vi của tam giác ABC và tam giác A’B’C’ bằng k.
Lời giải:
Ta có: . Do đó
Mặt khác, DB2 = AD.CD nên
Suy ra
Do đó ∆BAD ᔕ ∆CBD.
Nên (hai góc tương ứng)
Vậy DB là tia phân giác của góc ADC.
Lời giải:
Gọi H’’ là điểm đối xứng với H qua K. Khi đó KH = KH’’.
Xét ∆IKH và ∆IKH’’ có:
; IK là cạnh chung; KH = KH’’.
Do đó ∆IKH = ∆IKH’’ (hai cạnh góc vuông)
Suy ra IH = IH’’ (hai cạnh tương ứng)
Nên tam giác IHH’’ cân tại I.
Lại có nên tam giác IHH’’ đều.
Suy ra IH = HH’’
Mà HH’’ = 2HK nên IH = 2HK.
Đặt HK = a (a > 0). Khi đó IH = 2a.
Xét ∆IKH có nên ∆IKH vuông tại K, theo định lí Pythagore ta có:
IH2 = IK2 + KH2
Suy ra IK2 = IH2 – KH2 = (2a)2 – a2 = 3a2
Do đó
Tương tự, tam giác I’K’H’ có độ dài các cạnh là H’K’ = b (b > 0), I’H’ = 2b và
Suy ra
Do đó ∆I’K’H’ ᔕ ∆IKH (c.c.c).
Lời giải:
Nhận thấy:
Do đó
Xét ∆DBC và ∆BCA có:
và
Suy ra ∆DBC ᔕ ∆BCA (cạnh huyền và cạnh góc vuông tương ứng tỉ lệ).
Vậy ∆DBC ᔕ ∆BCA.
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Lý thuyết Trường hợp đồng dạng thứ nhất của tam giác
1. Trường hợp đồng dạng thứ nhất: Cạnh – cạnh – cạnh
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
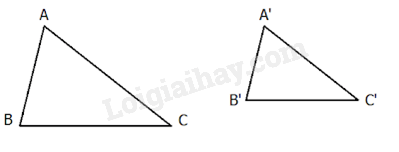
2. Trường hợp đồng dạng thứ nhất của tam giác vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
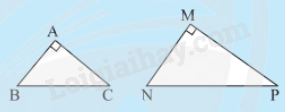
(ch.cgv)