Với giải sách bài tập Toán 8 Bài 9: Hình đồng dạng sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 9: Hình đồng dạng
Tìm khẳng định sai trong các khẳng định sau:
a) Hai đoạn thẳng EF và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.
b) Hai đoạn thẳng MP và AE đồng dạng phối cảnh, điểm B là tâm đồng dạng phối cảnh và
c) Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.
Lời giải:
⦁ Xét ∆ABC có E, F lần lượt là trung điểm của BC, AC nên
Ta thấy hai đường thẳng AF và BE cùng đi qua điểm C và nên hai đoạn thẳng EF và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh. Do đó khẳng định a) là đúng.
⦁ Ta có
Suy ra
Hay Do đó khẳng định b) sai.
⦁ Ta có nên
Do đó hay
Ta thấy hai đường thẳng RF và PB cùng đi qua điểm E và nên hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh. Do đó khẳng định c) đúng.
Vậy chỉ có khẳng định b) sai.
a) Tam giác M’N’P’ có đồng dạng phối cảnh với tam giác MNP hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.
b) Hãy chỉ ra đoạn thẳng AB sao cho hai đoạn thẳng AB và MP đồng dạng phối cảnh, điểm O là tâm đồng dạng phối cảnh và
Lời giải:
a) Ta thấy ba đường thẳng MM’, NN’, PP’ cùng đi qua điểm O và nên tam giác M’N’P’ đồng dạng phối cảnh với tam giác MNP và O là tâm đồng dạng phối cảnh.
b)
Gọi KH là đường trung bình của tam giác MOP (K ∈ OM, H ∈ OP).
Lấy A, B lần lượt là trung điểm của OK, OH.
Khi đó ; nên
Ta thấy hai đường thẳng AM và BP cùng đi qua điểm O và nên hai đoạn thẳng AB và MP đồng dạng phối cảnh, điểm O là tầm đồng dạng phối cảnh với .
a) Cho biết hai tứ giác ABCD và A’B’C’D’ có đò̀ng dạng phối cảnh hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.
b) Tứ giác A’B’C’D’ có là hình chữ nhật hay không, nếu tứ giác ABCD là hình chữ nhật? Vì sao?
Lời giải:
a) Xét ∆IA’B’ có A, B lần lượt là trung điểm của IA’, IB’ nên
Tương tự, ta sẽ có
Ta thấy bốn đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm I và nên tứ giác ABCD đồng dạng phối cảnh với tứ giác A’B’C’D’ và I là tâm đồng dạng phối cảnh.
b) Xét ∆IA’B’ có A, B lần lượt là trung điểm của IA’, IB’ nên AB là đường trung bình của ∆IA’B’. Do đó AB// A’B’ và
Tương tự, ta sẽ có:
Do ABCD là hình chữ nhật nên AB = CD, AD = BC.
Suy ra A’B’ = C’D’, A’D’ = B’C’.
Do đó, tứ giác A’B’C’D’ là hình bình hành.
Mặt khác, AB // A’B’ và BC // B’C’ nên
Do đó, hình bình hành A’B’C’D’ là hình chữ nhật.
Bài 53 trang 82 SBT Toán 8 Tập 2: Tìm khẳng định đúng trong các khẳng định sau:
a) Hai hình đồng dạng phối cảnh (hay vị tự) không là hai hình đồng dạng.
b) Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A’B’ đồng dạng phối cảnh thì AB // A’B’.
c) Hình ϰ’ gọi là đồng dạng với hình ϰ nếu hình ϰ’ bằng một hình nào đó đồng dạng phối cảnh với hình ϰ.
Lời giải:
⦁ Hai hình đồng dạng phối cảnh (hay vị tự) là hai hình đồng dạng. Do đó phát biểu a) sai.
⦁ Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A’B’ đồng dạng phối cảnh thì , do đó AB // A’B’ hoặc AB trùng A’B’. Do đó phát biểu b) sai.
⦁ Hình ϰ’ gọi là đồng dạng với hình ϰ nếu hình ϰ’ bằng một hình nào đó đồng dạng phối cảnh với hình ϰ. Do đó phát biểu c) đúng.
Vậy trong các phát biểu đã cho, phát biểu c) đúng.
a) Hai hình bình hành MNPQ và A’B’C’D’ có bằng nhau hay không;
b) Hai hình bình hành ABCD và A’B’C’D’ có đồng dạng hay không.
Lời giải:
a) Quan sát Hình 53, ta thấy hai hình bình hành MNPQ và A’B’C’D’ bằng nhau.
b) Ta thấy bốn đường thẳng AM, BN, CP, DQ cùng đi qua điểm I và nên hai hình bình hành ABCD, MNPQ đồng dạng phối cảnh và I là tâm đồng dạng phối cảnh.
Mặt khác, hai hình bình hành MNPQ và A’B’C’D’ bằng nhau.
Do đó, hình bình hành ABCD đồng dạng với hình bình hành A’B’C’D’.
a) Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với điểm D là tâm đồng dạng phối cảnh, tỉ số . Tìm độ dài các cạnh của tam giác A’B’C’.
b) Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm E là tâm đồng đạng phối cảnh, tỉ số . Tìm độ đài các cạnh của tam giác A’’B’’C’’.
c) Chứng minh diện tích tam giác A’B’C’ bằng diện tích tam giác A’’B’’C’’.
Lời giải:
a) Do tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC tỉ số nên
Mà AB = 13, BC = 14, CA = 15 nên:
; ;
Vậy A’B’ = 10,4; B’C’ = 11,2; C’A’ = 12.
b) Do tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC tỉ số nên
Mà AB = 13, BC = 14, CA = 15 nên:
; ;
Vậy A’’B’’ = 10,4; B’’C’’ = 11,2; C’’A’’ = 12.
c) Xét ∆A’B’C’ và ∆A’’B’’C’’ có:
A’B’ = A’’B’’ = 10;
B’C’ = B’’C’’ = 11,2;
A’C’ = A’’C’’ = 12;
Do đó ∆A’B’C’ = ∆A’’B’’C’’ (c.c.c).
Suy ra diện tích tam giác A’B’C’ bằng diện tích tam giác A’’B’’C’’.
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Lý thuyết Hình đồng dạng
1. Hình đồng dạng phối cảnh (hình vị tự)
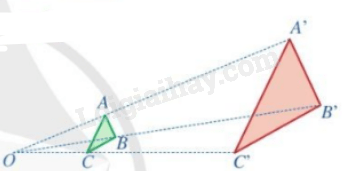
Hai tam giác A’B’C’ và ABC gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số gọi là tỉ số vị tự.
Tổng quát:
Bằng cách “phóng to” (nếu tỉ số vị tự k > 1) hay “thu nhỏ” (nếu tỉ số vị tự k < 1) hình H, ta sẽ nhận được hình H’ đồng dạng phối cảnh (hay vị tự) với hình H.
Ta gọi hình H’ là hình đồng dạng phối cảnh (hay vị tự) tỉ số k của hình H.
Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng AB là một đoạn thẳng A’B’ (nằm trên đường thẳng song song hoặc trùng với đường thẳng AB) và
2. Hình đồng dạng
Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.