Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác chi tiết sách Toán 8 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Giải Toán 8 trang 83 Tập 2

Khởi động trang 83 Toán 8 Tập 2: Bạn Khanh vẽ hai tam giác ABC và A’B’C’ sao cho $\widehat{A^{\text{'}}}=\hat{A}=60°$ và $\hat{B}=\widehat{B^{\text{'}}}=45°$ (Hình 79)

Hai tam giác A’B’C’ và ABC có đồng dạng hay không?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Xét ∆A’B’C’ và ∆ABC có:

$\widehat{A^{\text{'}}}=\hat{A}=60°$ và $\hat{B}=\widehat{B^{\text{'}}}=45°$

Suy ra ∆A’B’C’ ᔕ ∆ABC (g.g).

I. Trường hợp đồng dạng thứ ba: Góc-góc

Hoạt động 1 trang 83 Toán 8 Tập 2: Cho hai tam giác ABC, A’B’C’ sao cho: $\hat{A}=\widehat{A^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}}$ và A’B’ ≠ AB (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn: A’M = AB. Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh ∆A’MN = ∆ABC.

Từ đó suy ra ∆A’B’C’ ᔕ ∆ABC.

Lời giải:

Do MN // B’C’ nên $\widehat{A^{\text{'}}\mathrm{MN}}=\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ (hai góc đồng vị)

Mà $\widehat{\mathrm{ABC}}=\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ (giả thiết) nên $\widehat{A^{\text{'}}\mathrm{MN}}=\widehat{\mathrm{ABC}}.$

Xét ∆A’MN và ∆ABC có:

$\widehat{A^{\text{'}}\mathrm{MN}}=\widehat{\mathrm{ABC}};$

$\widehat{A^{\text{'}}}=\hat{A}$ (giả thiết).

Suy ra ∆A’MN = ∆ABC (g.c.g).

Do đó ∆A’MN ᔕ ∆ABC.

Lại có MN // B’C’ nên ∆A’B’C’ ᔕ ∆A’MN.

Từ đó ta suy ra ∆A’B’C’ ᔕ ∆ABC.

Luyện tập 1 trang 83 Toán 8 Tập 2: Cho hai tam giác ABC và MNP thỏa mãn: $\hat{A}=50°,$ $\hat{B}=60°,$ $\hat{N}=60°,$ $\hat{P}=70°.$ Chứng minh ∆ABC ᔕ ∆MNP.

Lời giải:

Xét∆ABC có: $\hat{A}+\hat{B}+\hat{C}=180°$ (tổng ba góc của một tam giác)

Suy ra $\hat{C}=180°-\hat{A}-\hat{B}=180°-50°-60°=70°.$

Xét ∆ABC và ∆MNP có: $\hat{B}=\hat{N}=60°;$ $\hat{C}=\hat{P}=70°.$

Suy ra ∆ABC ᔕ ∆MNP (g.g).

II. Áp dụng trường hợp đồng dạng thứ ba của tam giác vào tam giác vuông

Giải Toán 8 trang 84 Tập 2

Hoạt động 2 trang 84 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ có $\widehat{A^{\text{'}}}=\hat{A}=90°,$ $\widehat{B^{\text{'}}}=\hat{B}$ (Hình 84). Chứng minh ∆A’B’C’ ᔕ ∆ABC.

Lời giải:

Xét ∆A’B’C’ và ∆ABC có:

$\widehat{A^{\text{'}}}=\hat{A}=90°;\widehat{B^{\text{'}}}=\hat{B}$

Suy ra ∆A’B’C’ ᔕ ∆ABC (g.g).

Luyện tập 2 trang 84 Toán 8 Tập 2: Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh HA.HD = HB.HE.

Lời giải:

Do tam giác ABC có hai đường cao AD và BE nên BE ⊥ AC, AD ⊥ BC.

Suy ra $\widehat{\mathrm{AEB}}=\widehat{\mathrm{ADB}}=90°$ hay $\widehat{\mathrm{AEH}}=\widehat{\mathrm{BDH}}=90°$

Xét ∆HEA và ∆HDB có:

$\widehat{\mathrm{AEH}}=\widehat{\mathrm{BDH}}=90°;$

$\widehat{\mathrm{AHE}}=\widehat{\mathrm{BHD}}$ (đối đỉnh)

Suy ra ∆HEA ᔕ ∆HDB (g.g).

Do đó $\frac{\mathrm{HE}}{\mathrm{HD}}=\frac{\mathrm{HA}}{\mathrm{HB}}$ (tỉ số đồng dạng)

Vì vậy, HA.HD = HB.HE.

Bài tập

Giải Toán 8 trang 85 Tập 2

Bài 1 trang 85 Toán 8 Tập 2: Cho Hình 86.

a) Chứng minh ∆MNP ᔕ ∆ABC.

b) Tìm x.

Lời giải:

a) Xét ∆MNP và ∆ABC có:

$\hat{M}=\hat{A}=60°,$ $\hat{N}=\hat{B}=45°$

Suy ra ∆MNP ᔕ ∆ABC (g.g).

b) Vì ∆MNP ᔕ ∆ABC(câu a) nên $\frac{\mathrm{MP}}{\mathrm{AC}}=\frac{\mathrm{NP}}{\mathrm{BC}}$ (tỉ số đồng dạng)

Hay $\frac{x}{4\sqrt{2}}=\frac{3\sqrt{3}}{4\sqrt{3}}=\frac{3}{4}$

Do đó $x=\frac{4\sqrt{2}\cdot 3}{4}=3\sqrt{2}.$

Vậy $x=3\sqrt{2}.$

Bài 2 trang 85 Toán 8 Tập 2: Cho hai tam giác ABC và PMN thỏa mãn $\hat{A}=70°,$ $\hat{B}=80°,$ $\hat{M}=80°,$ $\hat{N}=30°.$ Chứng minh $\frac{\mathrm{AB}}{\mathrm{PM}}=\frac{\mathrm{BC}}{\mathrm{MN}}=\frac{\mathrm{CA}}{\mathrm{NP}}.$

Lời giải:

Xét ∆MNP có: $\hat{M}+\hat{N}+\hat{P}=180°$ (tổng ba góc của một tam giác)

Suy ra $\hat{P}=180°-\hat{M}-\hat{N}=180°-80°-30°=70°.$

Xét ∆ABC và ∆MNP có:

$\hat{A}=\hat{P}=70°;$

$\hat{B}=\hat{M}=80°$

Suy ra ∆ABC ᔕ ∆MNP (g.g)

Do đó $\frac{\mathrm{AB}}{\mathrm{PM}}=\frac{\mathrm{BC}}{\mathrm{MN}}=\frac{\mathrm{CA}}{\mathrm{NP}}$ (tỉ số đồng dạng).

Bài 3 trang 85 Toán 8 Tập 2: Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:

a) ∆ACD ᔕ ∆BCE và CA.CE = CB.CD.

b) ∆ACD ᔕ ∆AHE và AC.AE = AD.AH.

Lời giải:

a) Do tam giác ABC có hai đường cao AD và BE nên AD ⊥ BC, BE ⊥ AC.

Suy ra $\widehat{\mathrm{ADC}}=\widehat{\mathrm{BCE}}=90°;$ $\widehat{\mathrm{ADC}}=\widehat{\mathrm{AEH}}=90°$

Xét ∆ACD và ∆BCE có:

$\widehat{\mathrm{ADC}}=\widehat{\mathrm{BCE}}=90°;$ $\hat{C}$ là góc chung

Suy ra ∆ACD ᔕ ∆BCE (g.g).

Do đó $\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{CD}}{\mathrm{CE}}$ (tỉ số đồng dạng)

 Vì vậy, CA.CE = CB.CD.

b) Xét ∆ACD và ∆AHE có:

$\widehat{\mathrm{DAC}}$ là góc chung; $\widehat{\mathrm{ADC}}=\widehat{\mathrm{AEH}}=90°$

Suy ra∆ACD ᔕ ∆AHE (g.g).

Do đó $\frac{\mathrm{AC}}{\mathrm{AH}}=\frac{\mathrm{AD}}{\mathrm{AE}}$ (tỉ số đồng dạng)

Vì vậy, AC.AE = AH.AD.

Bài 4 trang 85 Toán 8 Tập 2: Cho Hình 87 với $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OCB}}.$ Chứng minh:

a) ∆OAD ᔕ ∆OCB;

b) $\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{\mathrm{OC}}{\mathrm{OB}};$

c) ∆OAC ᔕ ∆ODB.

Lời giải:

a) Xét ∆OAD và ∆OCB có:

$\hat{O}$ là góc chung; $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OCB}}$ (giả thiết)

Suy ra ∆OAD ᔕ ∆OCB (g.g).

b) Vì ∆OAD ᔕ ∆OCB(câu a)nên $\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OD}}{\mathrm{OB}}$ (tỉ số đồng dạng).

Do đó $\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{\mathrm{OC}}{\mathrm{OB}}$ (tính chất tỉ lệ thức).

c) Xét ∆OAC và ∆ODB có:

$\hat{O}$ là góc chung; $\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{\mathrm{OC}}{\mathrm{OB}}$ (câu a)

Suy ra∆OAC ᔕ ∆ODB (c.g.c).

Bài 5 trang 85 Toán 8 Tập 2:Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:

a) ∆ABC ᔕ ∆HBA và AB² = BC.BH;

b) ∆ABC ᔕ ∆HAC và AC² = BC.CH;

c) ∆ABH ᔕ ∆CAH và AH² = BH.CH;

d) $\frac{1}{{\mathrm{AH}}^2}=\frac{1}{{\mathrm{AB}}^2}+\frac{1}{{\mathrm{AC}}^2}.$

Lời giải:

a) Do tam giác ABC vuông tại A, có đường cao AH nên AH ⊥ BC

Do đó $\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHB}}=\widehat{\mathrm{AHC}}=90°$

Xét ∆ABC và ∆HBA có:

$\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHB}}=90°;$ $\hat{A}$ là góc chung

Suy ra ∆ABC ᔕ ∆HBA (g.g).

Do đó $\frac{\mathrm{AB}}{\mathrm{HB}}=\frac{\mathrm{BC}}{\mathrm{BA}}$ (tỉ số đồng dạng)

Nên AB² = BC.BH.

b) Xét ∆ABC và ∆HAC có:

$\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHC}}=90°;$ $\hat{C}$ là góc chung

Suy ra∆ABC ᔕ ∆HAC (g.g).

Do đó $\frac{\mathrm{AC}}{\mathrm{HC}}=\frac{\mathrm{BC}}{\mathrm{AC}}$(tỉ số đồng dạng)

Nên AC² = BC.CH.

c) Do ∆HBA ᔕ ∆ABC (do ∆ABC ᔕ ∆HBA (câu a)) và ∆ABC ᔕ ∆HAC (câu b)

Suy ra ∆HBAᔕ ∆HAC

Hay ∆ABH ᔕ ∆CAH

Suy ra $\frac{\mathrm{AH}}{\mathrm{CH}}=\frac{\mathrm{BH}}{\mathrm{AH}}$(tỉ số đồng dạng)

Nên AH² = BH.CH.

d) Ta có $\frac{1}{{\mathrm{AC}}^2}+\frac{1}{{\mathrm{AB}}^2}=\frac{1}{\mathrm{BC}\cdot \mathrm{CH}}+\frac{1}{\mathrm{BC}\cdot \mathrm{BH}}$

$=\frac{\mathrm{BH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}+\frac{\mathrm{CH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}$

$=\frac{\mathrm{BH}+\mathrm{CH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}=\frac{\mathrm{BC}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}$

$=\frac{1}{\mathrm{BH}\cdot \mathrm{CH}}=\frac{1}{{\mathrm{AH}}^2}.$

Vậy $\frac{1}{{\mathrm{AH}}^2}=\frac{1}{{\mathrm{AB}}^2}+\frac{1}{{\mathrm{AC}}^2}.$

Bài 6 trang 85 Toán 8 Tập 2: Cho Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là AH = 2,8 m và AK = 1,6 m. Em hãy tính chiều cao của cây.

Lời giải:

Xét ∆ABH và ∆CAH có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{CHA}}=90°;$  $\widehat{\mathrm{BAH}}=\widehat{\mathrm{ACH}}$(cùng phụ $\widehat{\mathrm{HAC}})$

Suy ra∆ABH ᔕ ∆CAH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{CH}}=\frac{\mathrm{BH}}{\mathrm{AH}}$(tỉ số đồng dạng)

Tứ giác AHBK có $\widehat{\mathrm{AHB}}=\widehat{\mathrm{HBK}}=\widehat{\mathrm{BKA}}=90°$ nên là hình chữ nhật

Suy ra BH = AK = 1,6 m.

Do đó $\mathrm{CH}=\frac{{\mathrm{AH}}^2}{\mathrm{BH}}=\frac{2,8^2}{1,6}=4,9$

Vì vậy, CB = CH + HB = 4,9 + 1,6 = 6,5 (m).

Vậy chiều cao của cây là 6,5 m.

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8

Lý thuyết Trường hợp đồng dạng thứ ba của tam giác

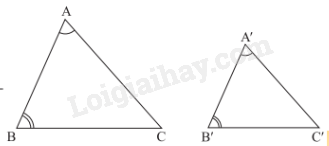
1. Trường hợp đồng dạng thứ ba (góc – góc)

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

$\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime },\widehat{A^{\prime }}=\hat{A},\widehat{B^{\prime }}=\hat{B}\\ \Rightarrow \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC\end{array}$

2. Trường hợp đồng dạng góc nhọn của tam giác vuông

Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

$\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }MNP,\hat{A}=\hat{M}={90}^0,\hat{B}=\hat{N}\\ \Rightarrow \mathrm{\Delta }ABC\backsim \mathrm{\Delta }MNP(g.g)\end{array}$