Sách bài tập Toán 8 Bài 7 (Cánh diều): Trường hợp đồng dạng thứ hai của tam giác

Admin Vietjack Ngày: 23-09-2024 Lớp 8

1.9 K

Với giải sách bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Giải SBT Toán 8 trang 75

Bài 37 trang 75 SBT Toán 8 Tập 2: Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng:

Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng trang 75

Lời giải:

Ta có $\frac{A B}{D E} = \frac{5}{3}; \frac{B C}{D F} = \frac{10}{6} = \frac{5}{3} .$

Do đó: $\frac{A B}{E D} = \frac{B C}{D F}$

Xét ∆ABC và ∆EDF có:

$\frac{A B}{E D} = \frac{B C}{D F}$ và $\hat{A B C} = \hat{E D F} = 60 °$

Suy ra ∆ABC ᔕ ∆EDF (c.g.c).

Bài 38 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC sao cho CD = 12 cm. Tính độ dài AD.

Lời giải:

Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC

Ta có: $\frac{A C}{D C} = \frac{18}{12} = \frac{3}{2}; \frac{C B}{C A} = \frac{27}{18} = \frac{3}{2}$ .

Suy ra $\frac{A C}{D C} = \frac{C B}{C A} = \frac{3}{2} .$

Xét ∆ACB và ∆DCA có:

$\frac{A C}{D C} = \frac{C B}{C A}$ và $\hat{A C B}$ là góc chung

Suy ra ∆ACB ᔕ ∆DCA (c.g.c).

Do đó $\frac{A C}{D C} = \frac{A B}{D A}$ (tỉ số đồng dạng)

Hay $\frac{18}{12} = \frac{12}{A D}$ nên $A D = \frac{12 \cdot 12}{18} = 8$ (cm).

Vậy AD = 8 cm.

Bài 39 trang 75 SBT Toán 8 Tập 2: Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD. Kẻ một đường thẳng tuỳ ý đi qua O và cắt cạnh AB tại M, CD tại N. Đường thẳng qua M song song với CD cắt AC tại E và đường thẳng qua N song song với AB cắt BD tại F. Chứng minh:

a) ∆OBE ᔕ ∆OFC;

b) BE // CF.

Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD

Lời giải:

a) Do NF // AB, mà M ∈ AB nên NF // MB.

Xét ∆OBM với NF // MB, ta có $\frac{O B}{O F} = \frac{O M}{O N}$ (hệ quả của định lí Thalès) (1).

Do ME // CD, mà N ∈ CD nên ME // NC.

Xét ∆OEM với ME // NC, ta có $\frac{O E}{O C} = \frac{O M}{O N}$ (hệ quả của định lí Thalès) (2).

Từ (1) và (2) ta có: $\frac{O B}{O F} = \frac{O E}{O C} (= \frac{O M}{O N})$

Xét ∆OBE và ∆OFC có:

$\hat{B O E} = \hat{F O C}$ (hai góc đối đỉnh) và $\frac{O B}{O F} = \frac{O E}{O C}$ (chứng minh trên)

Suy ra ∆OBE ᔕ ∆OFC (c.g.c).

b) Theo câu a, ta có ∆OBE ᔕ ∆OFC nên $\hat{E B O} = \hat{O F C}$ (hai góc tương ứng)

Mà hai góc $\hat{E B O}$ và $\hat{O F C}$ ở vị trí so le trong nên suy ra BE // CF.

Bài 40 trang 75 SBT Toán 8 Tập 2: Hình 38 cho biết tam giác ABC vuông ở A, AB = 5 cm, AC = 12 cm. Tam giác HAB vuông cân tại H, tam giác KAC vuông cân tại K. Các cặp tam giác sau có đồng dạng với nhau không? Vì sao?

a) Tam giác HAB và tam giác KAC.

b) Tam giác HKC và tam giác BAC.

Hình 38 cho biết tam giác ABC vuông ở A, AB = 5 cm, AC = 12 cm. Tam giác HAB

Lời giải:

a) • Tam giác HAB vuông cân tại H nên HA = HB và HA² + HB² = AB² (định lí Pythagore)

Do đó 2HA² = AB² = 5² = 25 hay $H A^{2} = H B^{2} = \frac{25}{2} = {(\frac{5}{\sqrt{2}})}^{2}$

Suy ra $H A = H B = \frac{5}{\sqrt{2}}$ (cm).

• Tam giác KAC vuông cân tại K nên KA = KC và KA² + KC² = AC² (định lí Pythagore)

Do đó 2KA² = AC² = 12² = 144 hay $K A^{2} = K B^{2} = \frac{144}{2} = {(\frac{12}{\sqrt{2}})}^{2}$

Suy ra $K A = K C = \frac{12}{\sqrt{2}}$ (cm).

Ta có: $\frac{H A}{K A} = \frac{\frac{5}{\sqrt{2}}}{\frac{12}{\sqrt{2}}} = \frac{5}{12}$ , $\frac{H B}{K B} = \frac{\frac{5}{\sqrt{2}}}{\frac{12}{\sqrt{2}}} = \frac{5}{12}$ , nên $\frac{H A}{K A} = \frac{H B}{K C}$

Xét ∆HAB và ∆KAC có:

$\hat{A H B} = \hat{A K C} = 90 °$ và $\frac{H A}{K A} = \frac{H B}{K C}$ (chứng minh trên)

Suy ra ∆HAB ᔕ ∆KAC (c.g.c).

b) Ta có: ∆AHB vuông cân tại H nên $\hat{H A B} = 45 °;$

∆AKC vuông cân tại K nên $\hat{K A C} = 45 ° .$

Do đó $\hat{H A K} = \hat{H A B} + \hat{B A C} + \hat{K A C}$ = $45 ° + 90 ° + 45 ° = 180 ° .$

Suy ra ba điểm H, A, K thẳng hàng.

Khi đó $H K = A H + A K$ = $\frac{5}{\sqrt{2}} + \frac{12}{\sqrt{2}} = \frac{17}{\sqrt{2}}$ (cm).

⦁ ∆HKC vuông tại K và có hai cạnh góc vuông là: $H K = \frac{17}{\sqrt{2}}$ (cm), $K C = \frac{12}{\sqrt{2}}$ (cm).

∆BAC vuông tại A và có hai cạnh góc vuông là AB = 5 cm, AC = 12 cm.

Ta có: $\frac{H K}{A B} = \frac{\frac{17}{\sqrt{2}}}{5} = \frac{17}{5 \sqrt{2}}$ , $\frac{K C}{A C} = \frac{\frac{12}{\sqrt{2}}}{12} = \frac{1}{\sqrt{2}}$

Ta thấy $\frac{H K}{A B} \neq \frac{K C}{A C}$

Do đó tam giác HKC không đồng dạng với tam giác BAC.

Bài 41 trang 75, 76 SBT Toán 8 Tập 2: Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, $\hat{A B D} = 90 °$ . Hai đường chéo AC và BD cắt nhau tại G. Điểm E nằm trên đường vuông góc với AC tại C thỏa mãn CE = AG và đoạn thẳng GE không cắt đường thẳng CD. Điểm F nằm trên đoạn thẳng DC và DF = GB. Chứng minh:

a) ∆FDG ᔕ ∆ECG;

b) ∆GDC ᔕ ∆GFE;

c) $\hat{G F E} = 90 ° .$

Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, góc ABD = 90 độ

Lời giải:

a) Xét ∆GDC với AB // CD, ta có $\frac{B G}{G D} = \frac{A G}{G C}$ (hệ quả của định lí Thalès)

Do đó $\frac{B G}{A G} = \frac{G D}{G C} .$

Mặt khác AG = CE, BG = DF nên $\frac{D F}{C E} = \frac{G D}{G C} .$

Xét ∆FDG và ∆ECG có:

$\hat{G D F} = \hat{G C E} = 90 °$ và $\frac{D F}{C E} = \frac{G D}{G C}$

Suy ra ∆FDG ᔕ ∆ECG (c.g.c).

b) Vì ∆FDG ᔕ ∆ECG (câu a) nên $\hat{D G F} = \hat{C G E}$ (hai góc tương ứng) và $\frac{D G}{C G} = \frac{G F}{G E}$ (tỉ số đồng dạng)

Từ $\hat{D G F} = \hat{C G E}$ ta có $\hat{D G F} + \hat{F G C} = \hat{C G E} + \hat{F G C}$ hay $\hat{D G C} = \hat{F G E} .$

Từ $\frac{D G}{C G} = \frac{G F}{G E}$ ta có $\frac{G D}{G F} = \frac{G C}{G E} .$

Xét ∆GDC và ∆GFE có:

$\hat{D G C} = \hat{F G E}$ và $\frac{G D}{G F} = \frac{G C}{G E}$ (chứng minh trên)

Suy ra ∆GDC ᔕ ∆GFE (c.g.c).

c) Vì ∆GDC ᔕ ∆GFE (câu b) nên $\hat{G D C} = \hat{G F E}$ (hai góc tương ứng)

Mà $\hat{G D C} = 90 °$ nên $\hat{G F E} = 90 ° .$

Giải SBT Toán 8 trang 76

Bài 42* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB. Chứng minh: $\hat{A D C} + \hat{A B C} = 45 °$ .

Lời giải:

Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB

Gọi E là trung điểm của AD nên AD = 2AE, AE = ED.

Mà AD = 2DB (giả thiết)

Suy ra AE = ED = DB

Do đó AB = AE + ED + BD = 3AE

Mà AB = 3AC (giả thiết) nên AE = AC hay AE = ED = DB = AC.

Đặt AE = x (x > 0).

Suy ra AE = ED = DB = AC = x, EB = 2x.

Xét ∆ACE vuông tại A, theo định lí Pythagore, ta có:

CE² = AC² + AE² = x² + x² = 2x²

Suy ra $C E = x \sqrt{2} .$

Ta có: $\frac{E D}{E C} = \frac{x}{x \sqrt{2}} = \frac{1}{\sqrt{2}}$ , $\frac{E C}{E B} = \frac{x \sqrt{2}}{2 x} = \frac{1}{\sqrt{2}}$ nên $\frac{E D}{E C} = \frac{E C}{E B}$

Xét ∆EDC và ∆ECB có:

$\hat{C E B}$ là góc chung và $\frac{E D}{E C} = \frac{E C}{E B}$ (chứng minh trên)

Suy ra ∆EDC ᔕ ∆ECB (c.g.c).

Do đó $\hat{E C D} = \hat{E B C}$ (hai góc tương ứng)

Vì vậy $\hat{A D C} + \hat{A B C} = \hat{E D C} + \hat{E B C} = \hat{E D C} + \hat{E C D}$

Mặt khác, $\hat{A E C}$ là góc ngoài tại đỉnh E của ∆CED nên $\hat{A E C} = \hat{E D C} + \hat{E C D}$

Do đó $\hat{A D C} + \hat{A B C} = \hat{A E C} .$

Lại có, do ∆AEC là tam giác vuông cân tại A nên $\hat{A E C} = 45 °$

Vậy $\hat{A D C} + \hat{A B C} = 45 °$ .

Bài 43* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 2 cm, AC = 3 cm, BC = 4 cm. Chứng minh: $\hat{B A C} = \hat{A B C} + 2 \hat{B C A} .$

Lời giải:

Cho tam giác ABC có AB = 2 cm, AC = 3 cm, BC = 4 cm

Trên đoạn thẳng BC lấy điểm D sao cho BD = 1 cm.

Suy ra CD = BC ‒ BD = 4 ‒ 1 = 3 cm.

Ta có: $\frac{B D}{B A} = \frac{1}{2}; \frac{A B}{C B} = \frac{2}{4} = \frac{1}{2}$ nên $\frac{B D}{B A} = \frac{A B}{C B} = \frac{1}{2} .$

Xét ∆ABD và ∆CBA có:

$\hat{A B C}$ là góc chung và $\frac{B D}{B A} = \frac{A B}{C B}$

Suy ra ∆ABD ᔕ ∆CBA (c.g.c).

Do đó $\hat{B A D} = \hat{B C A}$ (hai góc tương ứng) (1).

Tam giác ADC có CD = CA = 3 cm nên là tam giác cân tại C, do đó $\hat{D A C} = \hat{A D C}$ (2).

Từ (1) và (2), ta có:

$\hat{B A C} = \hat{B A D} + \hat{D A C} = \hat{B C A} + \hat{A D C} .$

Mặt khác, $\hat{A D C}$ là góc ngoài tại đỉnh D của ∆ABD nên $\hat{A D C} = \hat{B A D} + \hat{A B D} .$

Do đó $\hat{B A C} = \hat{B C A} + \hat{B A D} + \hat{A B D}$ = $\hat{B C A} + \hat{B C A} + \hat{A B C} = \hat{A B C} + 2 \hat{B C A}$

Vậy $\hat{B A C} = \hat{A B C} + 2 \hat{B C A}$ .

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài tập cuối chương 8

Lý thuyết Trường hợp đồng dạng thứ hai của tam giác

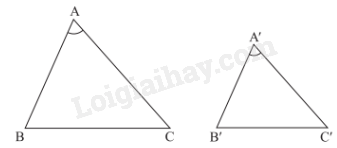
1. Trường hợp đồng dạng thứ hai: Cạnh – góc – cạnh

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.

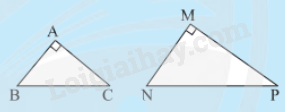
Lý thuyết Trường hợp đồng dạng thứ hai của tam giác (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

$\begin{array}{l} Δ A B C, Δ A^{'} B^{'} C^{'}, \frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C}, \hat{A^{'}} = \hat{A} \\ \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C (c . g . c) \end{array}$