Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Trường hợp đồng dạng thứ hai của tam giác được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Trường hợp đồng dạng thứ hai của tam giác. Mời các bạn đón xem:
Bài tập Toán 8 Trường hợp đồng dạng thứ hai của tam giác
A. Bài tập Trường hợp đồng dạng thứ hai của tam giác
Bài 1: Cho hình thoi ABCD cạnh a, có . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính .
Hướng dẫn giải:
Đáp án : C
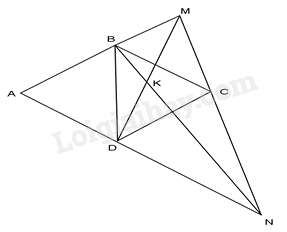
Do BC//AN (Vì ) nên ta có: (1)
Do CD//AM (Vì ) nên ta có: (2)
Từ (1) và (2)
có AB = AD (định nghĩa hình thoi) và nên là tam giác đều
Từ
Mặt khác
Xét và có:
Xét và có: chung
Vậy
Bài 2: Với AB//CD thì giá trị của x trong hình vẽ dưới đây là
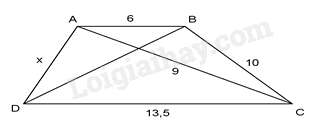
Hướng dẫn giải:
Đáp án : A
Ta có
Xét và có: (so le trong, AB//CD )
Bài 3: Biết và Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:
Hướng dẫn giải:
Đáp án : A
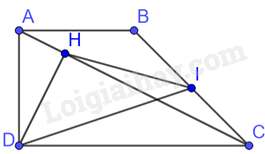
Áp dụng định lý Pythagore vào tam giác ADB vuông tại A có:
Tam giác ABD vuông cân tại A nên
Ta có: nên tam giác BDC vuông tại B, do đó,
Xét tam giác ADC và tam giác IBD có:
Do đó,
Suy ra,
Mà (cùng phụ với góc HDC)
Do đó,
Mà hay
Bài 4: Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng . Chu vi tam giác ABC là:
Hướng dẫn giải:
Đáp án : D
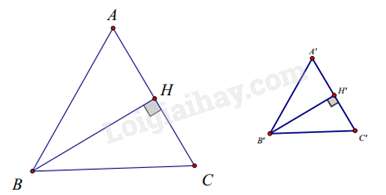
Tam giác BHC và tam giác B’H’C’ có:
Do đó,
Suy ra: +
+ , mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên
Do đó, nên
Theo tính chất dãy tỉ số bằng nhau ta có:
Mà chu vi tam giác A’B’C’ bằng 30cm nên chu vi tam giác ABC là:
Bài 5: Cho và có . Để cần thêm điều kiện là:
Hướng dẫn giải:
Đáp án : A
Ta có: và thì (c-g-c)
B. Lý thuyết Trường hợp đồng dạng thứ hai của tam giác
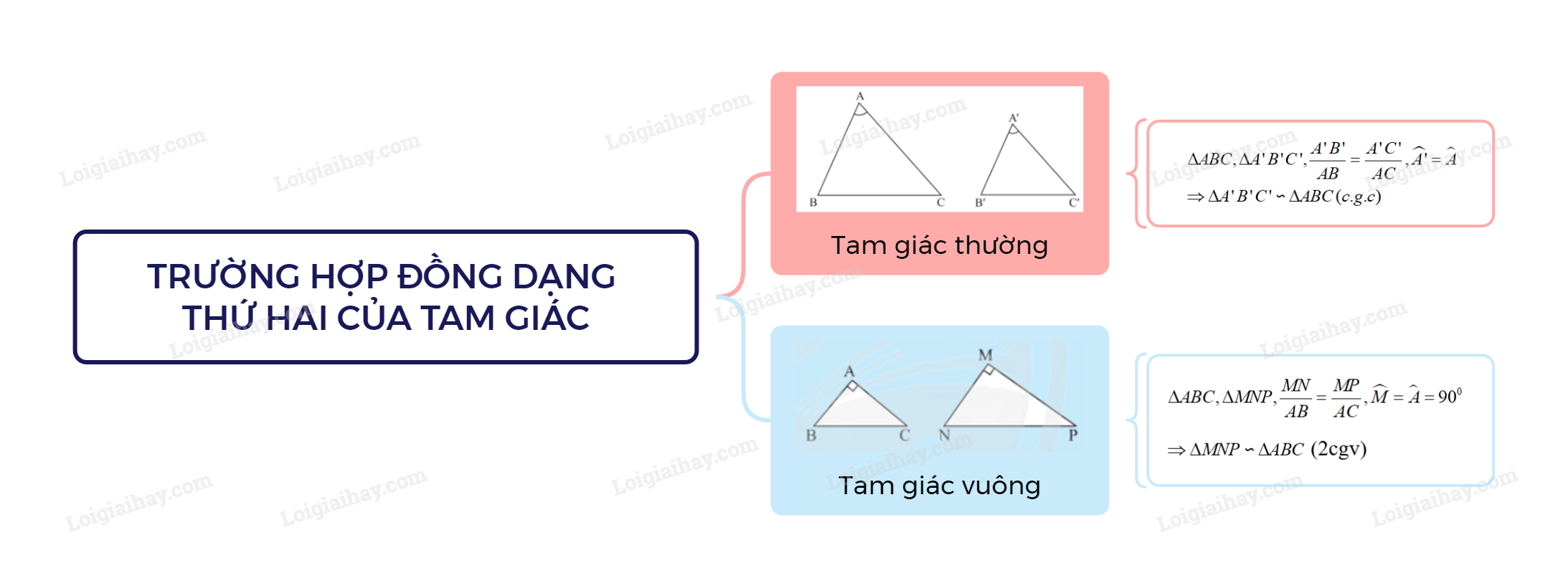
1. Trường hợp đồng dạng thứ hai: Cạnh – góc – cạnh
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
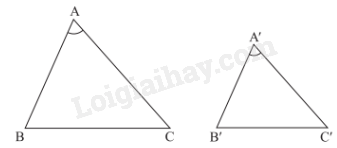
2. Trường hợp đồng dạng thứ hai của tam giác vuông
Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
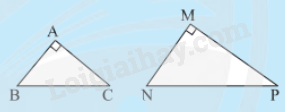
(2cgv)
Sơ đồ tư duy Trường hợp đồng dạng thứ hai của tam giác