Với giải Bài 42* trang 76 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 7: Trường hợp đồng dạng thứ hai của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 42* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB. Chứng minh: .
Lời giải:
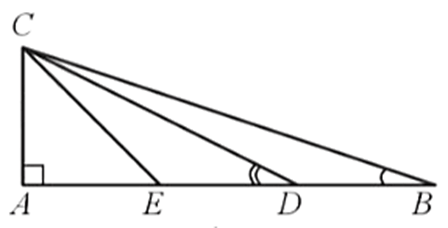
Gọi E là trung điểm của AD nên AD = 2AE, AE = ED.
Mà AD = 2DB (giả thiết)
Suy ra AE = ED = DB
Do đó AB = AE + ED + BD = 3AE
Mà AB = 3AC (giả thiết) nên AE = AC hay AE = ED = DB = AC.
Đặt AE = x (x > 0).
Suy ra AE = ED = DB = AC = x, EB = 2x.
Xét ∆ACE vuông tại A, theo định lí Pythagore, ta có:
CE2 = AC2 + AE2 = x2 + x2 = 2x2
Suy ra
Ta có: , nên
Xét ∆EDC và ∆ECB có:
là góc chung và (chứng minh trên)
Suy ra ∆EDC ᔕ ∆ECB (c.g.c).
Do đó (hai góc tương ứng)
Vì vậy
Mặt khác, là góc ngoài tại đỉnh E của ∆CED nên
Do đó
Lại có, do ∆AEC là tam giác vuông cân tại A nên
Vậy .
Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 37 trang 75 SBT Toán 8 Tập 2: Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng:....
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
