Với giải sách bài tập Toán 8 Bài 4: Tính chất đường phân giác của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 4: Tính chất đường phân giác của tam giác
a) Độ dài các đoạn thẳng AE, EC;
b) Khoảng cách từ O đến đường thẳng AC;
c) Độ dài đường phân giác AD (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười);
d) Diện tích tam giác DOE.
Lời giải:
a) Xét ∆ABC vuông tại A nên theo định lí Pythagore, ta có:
BC2 = AC2 + AB2 = 62 + 82 = 100, suy ra BC = 10 (cm).
Xét ∆ABC có BE là phân giác góc ABC nên (tính chất đường phân giác).
Suy ra
Vậy (cm); (cm).
b) Kẻ OH ⊥ AC tại H. Khi đó khoảng cách từ O đến đường thẳng AC là độ dài đoạn thẳng OH.
Ta có OH ⊥ AC, AB ⊥ AC nên OH // AB.
Xét ∆ABE với OH // AB, ta có: (định lí Thalès) (1).
Xét ∆AEB có AO là phân giác của góc CAB nên (tính chất đường phân giác)
Suy ra hay (2).
Từ (1) và (2) ta có , suy ra (cm).
c) Kẻ DK ⊥ AC, DI ⊥ AB, suy ra
Tứ giác AKDI có nên AKDI là hình chữ nhật
Lại có đường chéo AD là phân giác nên AKDI là hình vuông.
Suy ra AK = DK = DI.
Ta có S∆ABC = S∆ADC + S∆ADB nên
Hay AC.AB = AC.DK + AB.DI = (AB + AC).DK (do DK = DI).
Từ đó, ta có:
Xét ∆AKC vuông tại K có AD2 = AK2 + DK2 (định lí Pythagore)
Suy ra AD2 = AK2 + DK2 = DK2 + DK2 = 2DK2
Do đó (cm).
d) Ta có: (cm2).
Mà
Do đó (cm2).
Tương tự, ta có:
Xét ∆ABC có AD là đường phân giác của góc CAB nên (tính chất đường phân giác)
Suy ra hay
Nên
Suy ra (cm2)
Lại có
Suy ra (cm2).
Lời giải:
Trong ∆ABC có:
AD là phân giác góc A nên , suy ra hay (1)
CE là phân giác góc C nên , suy ra hay (2)
Từ (1) và (2) suy ra: .
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Vậy: AB = 2.10 = 20 cm;
BC = 2.12 = 24 cm;
AC = 2.15 = 30 cm.
a)
b) EF // AB.
Lời giải:
a) Tam giác ABD có AE là đường phân giác của góc A nên (1).
Tam giác ABC có BF là đường phân giác của góc B nên (2).
Vì ABCD là hình bình hành nên AD = BC, do đó (3)
Từ (1) và (2) suy ra
b) Ta có: suy ra hay
Gọi O là giao điểm hai đường chéo hình bình hành ABCD. Khi đó O là trung điểm của AC, BD nên BD = 2OD và AC = 2OC.
Do đó hay
Xét ∆ODC có nên EF // CD (định lí Thalès đảo)
Mà AB // CD (do ABCD là hình bình hành)
Do đó EF // AB.
Lời giải:
Ta có E nằm trên đường trung trực của đoạn AD nên EA = ED, do đó tam giác AED cân tại E.
Suy ra
Mà (do AD là đường phân giác của tam giác ABC)
Do đó
Lại có hai góc ở vị trí so le trong nên DE // AB.
Xét ∆ABC với DE // AB, ta có (hệ quả của định lí Thalès)
Mặt khác, do AD là đường phân giác của góc BAC nên
Nên
Suy ra , do đó
Vậy (cm).
Lời giải:
Ta có suy ra MD là đường phân giác của góc AMB.
Do đó
Vậy người đó có thể ước lượng được tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó bằng cách đo các khoảng cách DA, DB và tính
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 3: Đường trung bình của tam giác
Bài 4: Tính chất đường phân giác của tam giác
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Lý thuyết Tính chất đường phân giác của tam giác
Định lí
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
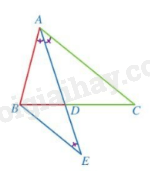
AD là đường phân giác của góc A trong ,
Ví dụ:
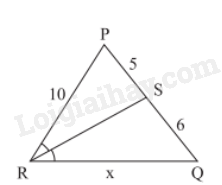
RS là tia phân giác của góc . Sử dụng tính chất đường phân giác, ta có:
Vậy độ dài đoạn thẳng RQ là 12.