Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 4: Tính chất đường phân giác của tam giác chi tiết sách Toán 8 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 4: Tính chất đường phân giác của tam giác
Tại sao ta luôn có tỉ lệ thức
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Do ABCD là hình vuông nên đường chéo AC là đường phân giác của góc BAD hay góc MAN.
Xét ∆AMN có AC là đường phân giác của góc MAN nên (tính chất đường phân giác).
a) Tính độ dài các đoạn thẳng DB, DC.
b) Tính độ dài các đoạn thẳng AB, AC.
c) So sánh các tỉ số
Lời giải:
a) Do mỗi ô vuông có độ dài cạnh bằng 1 cm nên:
⦁ Đoạn thẳng DB có độ dài bằng độ dài cạnh của 2 ô vuông nên DB dài 2 cm.
⦁ Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên DC dài 3 cm.
b) Ta thấy:
⦁ AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm.
⦁ AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AC dài 6 cm.
c) Ta có:
Vậy
Luyện tập 1 trang 67 Toán 8 Tập 2: Giải bài toán nêu trong phần mở đầu.
Lời giải:
Do ABCD là hình vuông nên đường chéo AC là đường phân giác của góc BAD hay góc MAN.
Xét ∆AMN có AC là đường phân giác của góc MAN nên (tính chất đường phân giác).
Lời giải:
Xét tam giác ABC có AD là đường phân giác nên (tính chất đường phân giác).
Mà AB < AC, suy ra
Do đó nên DB < DC.
Luyện tập 3 trang 68 Toán 8 Tập 2: Cho tam giác ABC có ba đường phân giác AD, BE, CE. Chứng minh
Lời giải:
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có:
(tính chất đường phân giác)
Do đó
Vậy
Lời giải:
Từ B kẻ đường thẳng song song với AC, cắt AD tại K.
Vì BK // AC nên theo hệ quả của định lí Thalès, ta có:
Mà (giả thiết) nên do đó BK = AB.
Khi đó tam giác ABK cân tại B nên
Mà BK // AC nên (hai góc so le trong)
Suy ra
Vậy AD là đường phân giác trong tam giác BAC.
Bài tập
Lời giải:
Áp dụng tính chất đường phân giác cho tam giác ABC, ta có:
⦁ (do AD là đường phân giác của góc BAC)
Suy ra hay
Do đó 6BD = 4(5 – BD)
6BD = 20 – 4BD
6BD + 4BD = 20
10BD = 20
BD = 2.
⦁ (do BE là đường phân giác của góc ABC)
Suy ra hay
Do đó 4CE = 5(6 – CE)
4CE = 30 – 5CE
4CE + 5CE = 30
9CE = 30
⦁ (do CF là đường phân giác của góc ACB)
Suy ra hay
Do đó 5AF = 6(4 – AF)
5AF = 24 – 6AF
5AF + 6AF = 24
11AF = 24
Lời giải:
Theo tính chất đường phân giác trong tam giác, ta có:
⦁ (do BE là đường phân giác của góc ABC trong ∆ABC);
⦁ (do BD là đường phân giác của góc ABM trong ∆ABM).
Mà BC = 2BM (do AM là đường trung tuyến của ∆ABC)
Suy ra
Vậy
Bài 3 trang 69 Toán 8 Tập 2: Quan sát Hình 43 và chứng minh
Lời giải:
⦁ (do AD là đường phân giác của góc BAC trong ∆ABC);
⦁ (do AE là đường phân giác của góc BAG trong ∆ABG).
Suy ra:
Vậy
Theo tính chất đường phân giác trong tam giác, ta có:
Lời giải:
Do ABCD là hình thoi nên AD = AB và AC là đường phân giác của góc BAC.
Xét ∆AMD có AN là đường phân giác góc MAD nên
Hay (vì AB = 3AM)
Do đó
Vậy ND = 3MN
a) Độ dài các đoạn thẳng BC, DB, DC;
b) Khoảng cách từ điểm D đến đường thẳng AC;
c) Độ dài đường phân giác AD.
Lời giải:
a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 25 = 52
Suy ra BC = 5.
Theo tính chất đường phân giác trong tam giác, ta có: (do AD là đường phân giác của góc BAC)
Suy ra hay
Do đó 4DB = 3(5 – DB)
4DB = 15 – 3DB
4DB + 3DB = 15
7DB = 15
Khi đó
Vậy
b) Kẻ DH ⊥ AC (H ∈ AC).
Suy ra DH // AB (cùng vuông góc với AC)
Áp dụng hệ quả của định lí Thalès trong tam giác ABC với DH // AB, ta có:
hay
Suy ra
Vậy khoảng cách từ điểm D đến đường thẳng AC là
c) Xét tam giác ABC với DH // AB, ta có: (hệ quả của định lí Thalès)
Hay suy ra
Xét tam giác AHD vuông tại H, ta có: AD2 = AH2 + DH2 (định lí Pythagore)
Suy ra
Do đó
Vậy độ dài đường phân giác AD là
Lời giải:
Theo tính chất đường phân giác trong hai tam giác ACD và BCD, ta có:
⦁ (do AE là đường phân giác của góc CAD);
⦁ (do BE là đường phân giác của góc CBD).
Suy ra
Vậy AD.BC = AC.BD.
Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Lý thuyết Tính chất đường phân giác của tam giác
Định lí
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
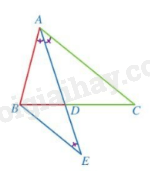
AD là đường phân giác của góc A trong ,
Ví dụ:
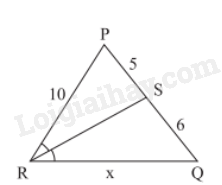
RS là tia phân giác của góc . Sử dụng tính chất đường phân giác, ta có:
Vậy độ dài đoạn thẳng RQ là 12.