Với giải sách bài tập Toán 8 Bài 2: Tứ giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 2: Tứ giác
Giải SBT Toán 8 trang 89
Bài 6 trang 89 SBT Toán 8 Tập 1: Tính các số đo ở các hình :
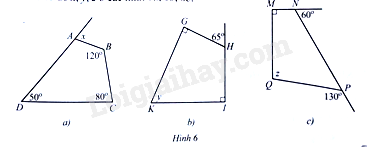
Lời giải:
a) Trong tứ giác , ta có: .
Do đó:
Ta có: (hai góc kề bù)
Suy ra
b) Ta có: (hai góc kề bù). Suy ra
Trong tứ giác , ta có:
Do đó: hay . Suy ra
c) Ta có: (hai góc kề bù). Suy ra
Ta lại có: (hai góc kề bù). Suy ra
Trong tứ giác , ta có:
Do đó hay . Suy ra .
.
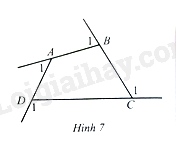
Lời giải:
Trong tứ giác , ta có:
Ta có: (các cặp góc kề bù)
Suy ra
Hay . Vậy .
Bài 8 trang 90 SBT Toán 8 Tập 1: a) Cho tứ giác có (Hình 8a). Tính số đo góc .
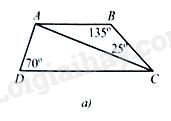
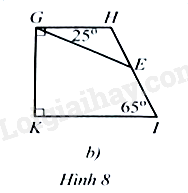
b) Cho tứ giác có . Trên lấy điểm sao cho (Hình 8b). Tính số đo góc .
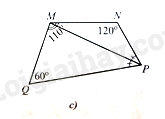
c) Cho tứ giác có là tia phân giác của góc (Hình 8c). Tính các số đo góc .
Lời giải:
a) Trong tam giác , ta có:
Do nên (hai góc so le trong)
Trong tam giác , ta có:
b) Trong tứ giác , ta có:
Trong tam giác , ta có:
Vậy
c) Trong tứ giác , ta có:
Do là tia phân giác của góc nên
Trong tam giác , ta có:
Lời giải:
Gọi là giao điểm của hai đường chéo và trong tứ giác .
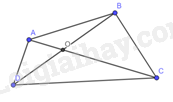
Xét tam giác , ta có:
Xét tam giác , ta có:
Suy ra
Hay
Tương tự ta cũng chứng minh được
Vậy: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.
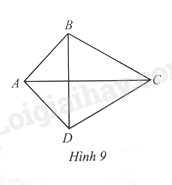
a) So sánh và .
b) Tìm mối liên hệ giữa hai đường chéo và
Lời giải:
Gọi là giao điểm của hai đường chéo và
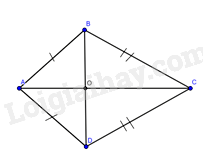
a) (c-c-c). suy ra
b) nên
. Suy ra
Mà nên
Vậy .
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
Lý thuyết Tứ giác
1. Khái niệm
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ:
Đặc điểm
+ Có 4 đỉnh
+ Có 4 cạnh
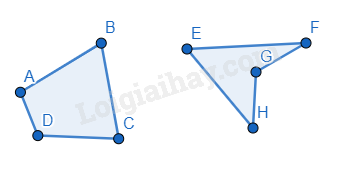
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất
+ Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng .
Tứ giác ABCD,
Ví dụ: