Giải SGK Toán 8 Bài 2 (Cánh diều): Tứ giác

Van Anh Ngày: 23-09-2024 Lớp 8

3.1 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 2: Tứ giác chi tiết sách Toán 8 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 2: Tứ giác

Giải Toán 8 trang 98 Tập 1

Khởi động trang 98 Toán 8 Tập 1: Hình ảnh thửa ruộng nhìn từ trên cao hay hình ảnh cánh diều (Hình 12) gợi lên những hình tứ giác.

Khởi động trang 98 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Tứ giác là hình có những tính chất gì?

Lời giải:

Sau bài học này chúng ta giải quyết được câu hỏi trên như sau:

Tứ giác là hình có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc trong đó:

• Hai cạnh kề nhau không cùng thuộc một đường thẳng;

• Không có ba đỉnh nào thẳng hàng.

• Tổng các góc của tứ giác bằng 360°.

I. Tứ giác

Hoạt động 1 trang 98 Toán 8 Tập 1: Quan sát tứ giác ABCD ở Hình 13 và đọc tên các cạnh, các đường chéo, các đỉnh, các góc của tứ giác đó.

Hoạt động 1 trang 98 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

Quan sát Hình 13, ta thấy tứ giác ABCD có:

• Các cạnh: AB, BC, CD, DA.

• Các đường chéo: AC, BD;

• Các đỉnh: A, B, C, D;

• Các góc: DAB, ABC, BCD, CDA;

Hoạt động 2 trang 98 Toán 8 Tập 1: Quan sát các hình 14a, 14b và nêu nhận xét về vị trí của mỗi tứ giác so với đường thẳng chứa một cạnh bất kì của tứ giác đó.

Hoạt động 2 trang 98 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

Tứ giác ABCD luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.

Tứ giác MNPQ không nằm về một phía của đường thẳng chứa cạnh NP hoặc cạnh PQ của tứ giác.

II. Tổng các góc của một tứ giác

Giải Toán 8 trang 99 Tập 1

Hoạt động 3 trang 99 Toán 8 Tập 1: Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD.

a) Gọi T₁ và T₂ lần lượt là tổng các góc của tam giác ABC và tam giác ACD. Tổng T₁ + T₂ bằng bao nhiêu độ?

b) Gọi T là tổng các góc của tứ giác ABCD. So sánh T với T₁ +T₂.

Hoạt động 3 trang 99 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

a) Xét tam giác ABC có: $\hat{B A C} + \hat{B} + \hat{B C D} = 180 °$ (định lí tổng các góc trong một tam giác).

Do đó T₁ = 180°.

Xét tam giác ACD có $\hat{D A C} + \hat{A C D} + \hat{D} = 180 °$ (định lí tổng các góc trong một tam giác).

Do đó T₂ = 180°.

Suy ra T₁ + T₂ = 180° + 180° = 360°.

b) Xét tứ giác ABCD ta có:

$T = \hat{A} + \hat{B} + \hat{C} + \hat{D}$

$= (\hat{B A C} + \hat{D A C}) + \hat{B} + (\hat{B C D} + \hat{A C D}) + \hat{D}$

$= 180 ° + 180 ° = 360 °$ .

Suy ra T = T₁ + T₂.

Giải Toán 8 trang 100 Tập 1

Luyện tập trang 100 Toán 8 Tập 1: Tìm x trong Hình 18.

Luyện tập trang 100 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$

Suy ra 85° + x + 65° + 75° = 360°

Do đó x = 360° – 85° – 65° – 75° = 135°.

Bài tập

Bài 1 trang 100 Toán 8 Tập 1: Trong các tứ giác ở hình 19a, 19b, 19c, 19d, 19e, 19g, tứ giác nào không phải là tứ giác lồi? Vì sao?

Bài 1 trang 100 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

Trong các tứ giác ở Hình 19, tứ giác ở hình 19c không phải là tứ giác lồi vì tứ giác này không nằm về một phía đối với hai đường thẳng chứa lần lượt hai cạnh của tứ giác (hai đường thẳng màu đỏ được vẽ ở hình bên dưới).

Bài 1 trang 100 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Bài 2 trang 100 Toán 8 Tập 1: a) Tứ giác ABCD có $\hat{A} + \hat{C} = 180 °$ > thì $\hat{B} + \hat{D}$ bằng bao nhiêu độ?

b) Có hay không một tứ giác có 2 góc tù và 2 góc vuông?

c) Có hay không một tứ giác có cả 4 góc đều là góc nhọn?

Lời giải:

a) Xét tứ giác ABCD có $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$

Suy ra $\hat{B} + \hat{D} = 360 ° - (\hat{A} + \hat{C}) = 360 ° - 180 ° = 180 °$ .

Vậy $\hat{B} + \hat{D} = 180 °$ .

b) Giả sử tứ giác ABCD có $\hat{A}, \hat{B}$ là hai góc tù và $\hat{C}, \hat{D}$ là hai góc vuông.

Tức là $\hat{A} > 90 °, \hat{B} > 90 °$ và $\hat{C} = \hat{D} = 90 °$ .

Ta có $\hat{A} + \hat{B} + \hat{C} + \hat{D} > 90 ° + 90 ° + 90 ° + 90 ° = 360 °$

Hay $\hat{A} + \hat{B} + \hat{C} + \hat{D} > 360 °$ không thỏa mãn định lí tổng các góc của một tứ giác.

Do đó không có tứ giác nào có 2 góc tù và 2 góc vuông.

c) Giả sử tứ giác ABCD có cả bốn góc $\hat{A}, \hat{B}, \hat{C}, \hat{D}$ đều là góc nhọn.

Tức là $\hat{A} < 90 °, \hat{B} < 90 °, \hat{C} < 90 °, \hat{D} < 90 °$ .

Ta có $\hat{A} + \hat{B} + \hat{C} + \hat{D} < 90 ° + 90 ° + 90 ° + 90 ° = 360 °$

Hay $\hat{A} + \hat{B} + \hat{C} + \hat{D} < 360 °$ không thỏa mãn định lí tổng các góc của một tứ giác.

Do đó không có tứ giác nào có cả 4 góc đều là góc nhọn.

Bài 3 trang 100 Toán 8 Tập 1: Hình 20 mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thuỷ. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó (làm tròn kết quả đến hàng phần mười của mét).

Bài 3 trang 100 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

Giả sử mặt cắt dọc phần nổi trên mặt nước cả tàu thủy được mô tả như hình vẽ dưới đây:

Bài 3 trang 100 Toán 8 Tập 1 Cánh diều | Giải Toán 8

• Do tam giác AHB vuông tại H nên theo định lí Pythagore ta có:

AB² = AH² + HB² = 5,6² + 8,4² = 31,36 + 70,56 = 101,92

Suy ra $A B = \sqrt{101,92} (m)$ .

• Do tam giác CDK vuông tại K nên theo định lí Pythagore ta có:

CD² = CK² + KD² = 16,2² + 10,8² = 262,44 + 116,64 = 379,08

Suy ra $C D = \sqrt{379,08} (m)$ .

• Ta có AI = HK = HB + BC + CK = 8,4 + 24 + 16,2 = 48,6 (m).

DI = DK – IK = DK – AH = 10,8 – 5,6 = 5,2 (m).

Do tam giác ADI vuông tại I nên theo định lí Pythagore ta có:

AD² = AI² + DI² = 48,6² + 5,2² = 2 361,96 + 27,04 = 2 389

Suy ra $A D = \sqrt{2 389} (m)$ .

• Chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó là:

AB + BC + CD + DA = $\sqrt{101,92} + 24 + \sqrt{379,08} + \sqrt{2389}$ ≈ 102,4 (m).

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Lý thuyết Tứ giác

1. Khái niệm

Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Ví dụ:

(ảnh 1)

Đặc điểm

+ Có 4 đỉnh

+ Có 4 cạnh

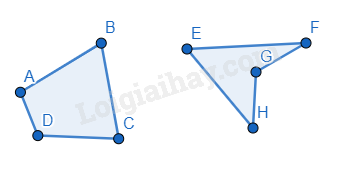
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.

Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.

2. Tính chất

+ Hai cạnh kề nhau là hai cạnh chung đỉnh.

+ Hai cạnh kề nhau tạo thành góc của tứ giác.

+ Hai cạnh đối nhau không chung đỉnh.

+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.

+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.

3. Định lí tổng các góc của một tứ giác

Tổng số đo các góc của một tứ giác bằng $360^{0}$ .

Tứ giác ABCD, $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360^{0}$

Ví dụ:

(ảnh 2)

$\hat{B} = 360^{0} - 93^{0} - 123^{0} - 75^{0} = 69^{0}$

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

132

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm