Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối

Van Anh Ngày: 05-09-2023 Lớp 8

774

Với giải Bài 9 trang 90 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 2: Tứ giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 2: Tứ giác

Bài 9 trang 90 SBT Toán 8 Tập 1: Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

Lời giải:

Gọi $O$ là giao điểm của hai đường chéo $A C$ và $B D$ trong tứ giác $A B C D$ .

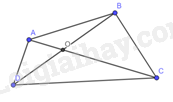
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 6)

Xét tam giác $O A B$ , ta có: $O A + O B > A B$

Xét tam giác $O C D$ , ta có: $O C + O D > C D$

Suy ra $O A + O B + O C + O D > A B + C D$

Hay $A C + B D > A B + C D$

Tương tự ta cũng chứng minh được $A C + B D > A D + B C$

Vậy: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 6 trang 89 SBT Toán 8 Tập 1: Tính các số đo $x, y, z$ ở các hình $6 a, 6 b, 6 c$ :...

Bài 7 trang 90 SBT Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác $A B C D$ ở Hình 7 (tại mỗi đỉnh chỉ nhọn một góc ngoài)....

Bài 8 trang 90 SBT Toán 8 Tập 1: a) Cho tứ giác $A B C D$ có $A B / / C D, \hat{B} = 135^{\circ}, \hat{D} = 70^{\circ}, \hat{A C B} = 25^{\circ}$ (Hình 8a). Tính số đo góc $D A C$ ....

Bài 9 trang 90 SBT Toán 8 Tập 1: Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối....

Bài 10 trang 90 SBT Toán 8 Tập 1: Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới. Một tứ giác $A B C D$ với $A B = A D, B C = C D$ gọi là hình “chiếc diều” (Hình 9)....

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

226

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

190

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

150

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

146

Tìm kiếm