Với giải sách bài tập Toán 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ
Bài 19 trang 17 Toán 7 Tập 1: Tính:
a) 25; b) (−5)3; c) (0,4)3; d) (−0,4)3;
e) ; g) ; h) (21,5)0; i) .
Lời giải:
a) 25 = 2 . 2 . 2 . 2 . 2 = 32;
b) (−5)3 = (−5) . (−5) . (−5) = −125;
c) (0,4)3 = (0,4) . (0,4) . (0,4) = 0,064;
d) (−0,4)3 = (−0,4) . (−0,4) . (−0,4) = −0,064;
e) ;
g) ;
h) (21,5)0 = 1;
i) .
Bài 20 trang 17 Toán 7 Tập 1: Chọn từ "bằng nhau", "đối nhau" thích hợp cho :
a) Nếu hai số đối nhau thì bình phương của chúng ;
b) Nếu hai số đối nhau thì lập phương của chúng ;
c) Lũy thừa chẵn cùng bậc của hai số đối nhau thì ;
d) Lũy thừa lẻ cùng bậc của hai số đối nhau thì .
Lời giải:
a) Nếu hai số đối nhau thì bình phương của chúng bằng nhau;
b) Nếu hai số đối nhau thì lập phương của chúng đối nhau;
c) Lũy thừa chẵn cùng bậc của hai số đối nhau thì bằng nhau;
d) Lũy thừa lẻ cùng bậc của hai số đối nhau thì đối nhau.
Bài 21 trang 18 Toán 7 Tập 1: Cho các đẳng thức sau:
a) 102 . 103 = 106;
b) (1,2)8 : (1,2)4 = (1,2)2;
c) ;
d) ;
e) 561 : (−5)60 = 5;
g) (−0,27)3 . (−0,27)2 = (0,27)5.
Bạn Đức phát biểu: "Trong các đẳng thức trên, chỉ có một đẳng thức đúng". Theo em, phát biểu của bạn Đức đúng không? Vì sao?
Lời giải:
Ta có:
a) 102 . 103 = 102 + 3 = 105;
b) (1,2)8 : (1,2)4 = (1,2)8 – 4 = (1,2)4;
c) ;
d) và ;
e) 561 : (−5)60 = 561 : 560 = 561 – 60 = 51 = 5;
g) (−0,27)3 . (−0,27)2 = (−0,27)3 + 2 = (−0,27)5.
Do đó chỉ đẳng thức ở câu e đúng.
Vậy phát biểu của bạn Đức là đúng.
Bài 22 trang 18 Toán 7 Tập 1: Viết mỗi số sau dưới đây dưới dạng lũy thừa với cơ số cho trước:
a) 343 với cơ số 7;
b) 0,36 với cơ số 0,6 và −0,6;
c) với cơ số ;
d) 1,44 với cơ số 1,2 và −1,2.
Lời giải:
a) 343 viết dưới dạng lũy thừa với cơ số 7 là: 343 = 73;
b) 0,36 viết dưới dạng lũy thừa với cơ số 0,6 và −0,6 là:
0,36 = (0,6)2 = (−0,6)2;
c) viết dưới dạng lũy thừa với cơ số là: ;
d) 1,44 viết dưới dạng lũy thừa với cơ số 1,2 và −1,2 là:
1,44 = (1,2)2 = (−1,2)2.
Bài 23 trang 18 Toán 7 Tập 1: Tìm số thích hợp cho :
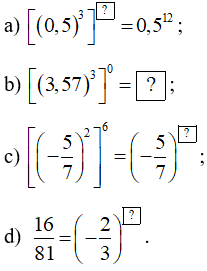
Lời giải:
a)
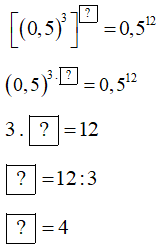
Vậy .
b)
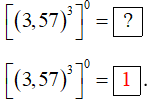
c)
Vậy .
d)
Vậy .
Bài 24 trang 18Toán 7 Tập 1:So sánh:
a) (−0,1)2 . (−0,1)4 và ;
b) và ;
c) 98 : 273 và 32 . 35;
d) và ;
e) và .
Lời giải:
a) Ta có (−0,1)2 . (−0,1)4 = (−0,1)2 + 4 = (−0,1)6;
.
Vậy .
b)
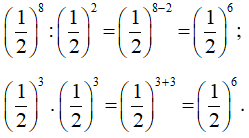
Vậy .
c) 98 : 273 =
= 316 : 39 = 316 – 9 = 37;
32 . 35 = 32 + 5 = 37.
Vậy 98 : 273 = 32 . 35.
d)
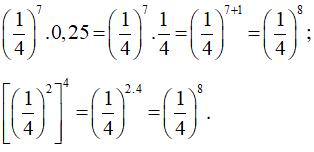
Vậy = .
e)
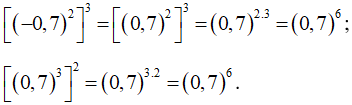
Vậy = .
Bài 25 trang 18 Toán 7 Tập 1: Viết kết quả mỗi phép tính sau dưới dạng lũy thừa của a:
a) với ;
b) với a = 0,75;
c) với ;
d) với a = 2.
Lời giải:
a)
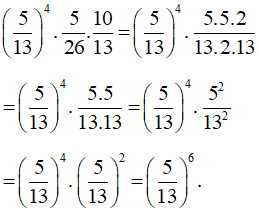
b)
= (0,75)4 . (0,75)3 = (0,75)4 + 3 = (0,75)7.
c)
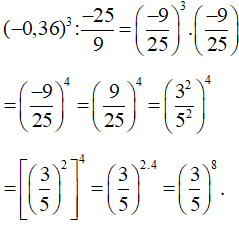
d)
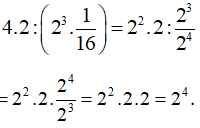
Bài 26 trang 19 Toán 7 Tập 1: Tìm số hữu tỉ x, biết:
a) ;
b) (0,09)3 : x = − (0,09)2.
Lời giải:
a)
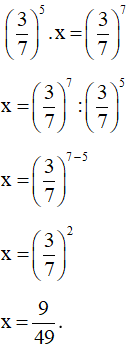
Vậy .
b) (0,09)3 : x = − (0,09)2.
x = (0,09)3 : [− (0,09)2]
x = −[(0,09)3 : (0,09)2]
x = −[(0,09)3 – 2]
x = −0,09.
Vậy x = −0,09.
Bài 27 trang 19 Toán 7 Tập 1: So sánh:
a) và ;
b) 2433 và 1252.
Lời giải:
a) và
Nhận xét: Với hai số tự nhiên m, n thỏa mãn m > n > 0, ta có:
∙ Nếu 0 < x < 1 thì xm < xn;
∙ Nếu x > 1 thì xm > xn.
Do và 40 < 50 nên >
b) 2433 và 1252.
Nhận xét: Với số tự nhiên m > 0 và hai số hữu tỉ a, b thỏa mãn a > b > 0, ta có: am > bm.
Ta có: 2433 = và 1252 = .
Do 3 < 5 nên 315 < 515.
Vậy 2433 < 1252.
Bài 28 trang 19 Toán 7 Tập 1: Bạn Na viết một trang web để kết bạn. Trang web đã nhận được 3 lượt truy cập trong tuần đầu tiên. Nếu số lượt truy cập tuần tiếp theo gấp 3 lần số lượt truy cập tuần trước thì sau 6 tuần đầu tiên, trang web của bạn Na có tất cả bao nhiêu lượt truy cập?
Lời giải:
Số lượt truy cập trag web của bạn Na trong tuần thứ nhất là 3 lượt; tuần thứ hai là 32 lượt; …; tuần thứ sáu là 36 lượt.
Như vậy, sau 6 tuần đầu tiên, số lượt truy cập trang web của bạn Na có tất cả là:
3 + 32 + 33 + 34 + 35 + 36
= 3 + 6 + 27 + 81 + 243 + 729 = 1 092 (lượt).
Vậy sau 6 tuần đầu tiên, số lượt truy cập trang web của bạn Na có tất cả là: 1 092 lượt.
a) Rút gọn biểu thức A = 1 + 2 + 21 + 22 + … + 225.
b) Một công ty phát triển kĩ thuật số có một thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 26 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
- Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 50 triệu đồng.
- Phương án 2: Ngày đầu nhận 1 đồng, ngày sau nhận gấp đôi ngày trước đó.
Theo em, phương án nào nhận được nhiều tiền hơn? Vì sao?
Lời giải:
a) Ta có: A = 1 + 2 + 21 + 22 + … + 225.
2A = 2 . (1 + 2 + 21 + 22 + … + 225) = 2 + 21 + 22 + … + 226.
Suy ra 2A – A = (2 + 21 + 22 + … + 226) – (1 + 2 + 21 + 22 + … + 225)
= 2 + 21 + 22 + … + 226 – 1 – 2 – 21 – 22 – … – 225
= (2 – 2) + (21 – 21) + (22 – 22) + … (225 – 225) + 226 – 1.
= 226 – 1.
Vậy A = 226 – 1.
b) Theo phương án 2 ta có: Số tiền nhận ngày thứ nhất là 1 đồng; ngày thứ hai là 2 đồng; ngày thứ ba là 22 đồng; ngày thứ tư là 23 đồng; … ; ngày thứ hai mươi sáu là 225 đồng.
Như vậy, số tiền công nhận được theo phương án 2 là:
1 + 2 + 21 + 22 + … + 225 = 226 – 1 = 67 108 863 (đồng).
Do 50 000 000 < 67 108 863 nên phương án 2 nhận được nhiều tiền công hơn.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ
Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc
Bài 5: Biểu diễn thập phân của số hữu tỉ
Lý thuyết Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ
1. Phép tính lũy thừa với số mũ tự nhiên
- Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x: với
Số x được gọi là cơ số, n gọi là số mũ.
- Quy ước x1 = x.
Chú ý:
xn đọc là “x mũ n” hoặc “x lũy thừa n” hoặc “lũy thừa bậc n của x”.
x2 còn được gọi là “x bình phương” hay “bình phương của x”.
x3 còn gọi là “x lập phương” hay “lập phương của x”.
Ví dụ:
a)
b) (0,2) . (0,2) . (0,2) = (0,2)3
Chú ý: Để viết lũy thừa bậc n của phân số , ta phải viết trong dấu ngoặc ( ), tức là .
2. Tích và thương của hai lũy thừa cùng cơ số
- Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
xm . xn = xm+n
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia :
xm : xn = xm – n
- Quy ước x0 = 1 (x ≠ 0).
Ví dụ:
a)
b) (–0,5)4 : (–0,5)4 = (–0,5)4 – 4 = (–0,5)0 = 1.
3. Lũy thừa của một lũy thừa
Khi tính lũy thừa của một lũy thừa ta giữ nguyên cơ số và nhân hai số mũ:
Ví dụ: .