Với giải sách bài tập Toán 7 Bài tập cuối chương 1 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài tập cuối chương 1
Bài 45 trang 25 Toán 7 Tập 1: Trong Hình 9, điểm nào biểu diễn số hữu tỉ trên trục số?

A. Điểm M.
B. Điểm N.
C. Điểm P.
D. Điểm Q.
Lời giải:
Ta thấy nên điểm biểu diễn số hữu tỉ nằm bên phải số 1 trên trục số.
Trên trục số Hình 9 chỉ có điểm Q nằm bên phải số 1 nên điểm Q biểu diễn số hữu tỉ .
Chọn đáp án D.
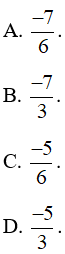
Lời giải:
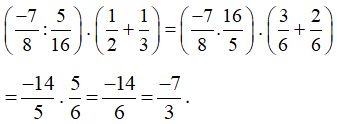
Chọn đáp án B.
Bài 47 trang 25 Toán 7 Tập 1: Giá trị của x trong đẳng thức (3x – 2)2 = 2 . 23 là:
A. 2.
B. và 2.
C. và 2.
D. và 2.
Lời giải:
(3x – 2)2 = 2 . 23
(3x – 2)2 = 16
(3x – 2)2 = 42
Trường hợp 1: 3x – 2 = 4
3x = 4 + 2
3x = 6
x = 2.
Trường hợp 1: 3x – 2 = –4
3x – 2 = –4
3x = –4 + 2
3x = –2
.
Vậy .
Chọn đáp án C.
Trong các phân số , phân số viết được dưới dạng số thập phân vô hạn tuần hoàn là:
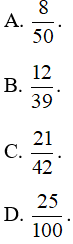
Lời giải:
Ta có:
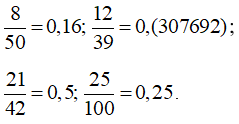
Trong các phân số , phân số viết được dưới dạng số thập phân vô hạn tuần hoàn.
Chọn đáp án B.

Lời giải:
Ta có: .
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng đơn vị cũ).
Đi theo ngược chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 2 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ hay .
Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 đơn vị mới đến điểm B. Điểm B biểu diễn số hữu tỉ .
Điểm C biểu diễn số hữu tỉ 1.
Ta biểu diễn các điểm A, B, C trên trục số như sau:
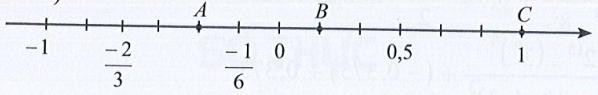
a) Sắp xếp các số sau theo thứ tự tăng dần: .
b) Sắp xếp các số sau theo thứ tự giảm dần: .
Lời giải:
a) ∙ Nhóm các số hữu tỉ âm: .
Ta có .
Vì −3,7 < −2,1(6) < −0,2 nên .
∙ Nhóm các số hữu tỉ dương: .
Ta thấy: .
Ta có ; .
Vì 33 < 42 nên .
Do đó .
Từ đó suy ra .
Vậy các số được sắp xếp theo thứ tự tăng dần là:
b) ∙ Nhóm các số hữu tỉ âm: .
Ta có .
Vì nên suy ra .
∙ Nhóm các số hữu tỉ dương: .
Ta có: .
Vì 2,45 > 2,2 > 0,3541(5) nên .
Do đó .
Vậy các số được sắp xếp theo thứ tự giảm dần: .
Bài 51 trang 25 Toán 7 Tập 1: Tính giá trị của mỗi biểu thức sau:
a) ;
b) ;
c) ;
d) (0,1)21 : (−0,01)10.
Lời giải:
a) ;
b)
= −10 + 0,2 = −9,8;
c)
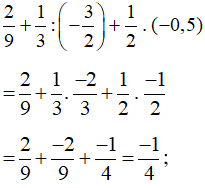
d) (0,1)21 : (−0,01)10
= (0,1)21 : (0,01)10
= (0,1)21 : (0,1)20 = 0,1.
Bài 52 trang 26 Toán 7 Tập 1: Tính một cách hợp lí:
a) ;
b) ;
c*) ;
d*) .
Lời giải:
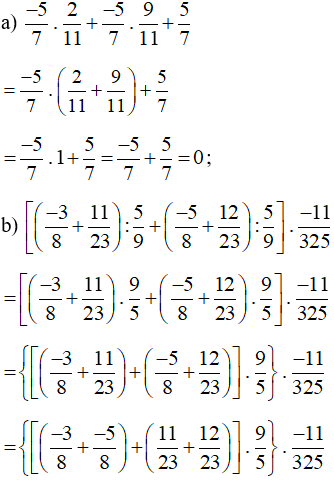
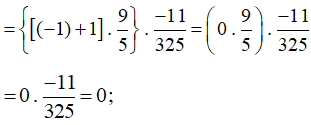
c*) Nhận xét: Với hai số hữu tỉ x, y ta có:
(x . y)n = xn . yn; (y ≠ 0).
Khi đó:
= 35 – (–1)2 = 243 – 1 = 242;
d*)
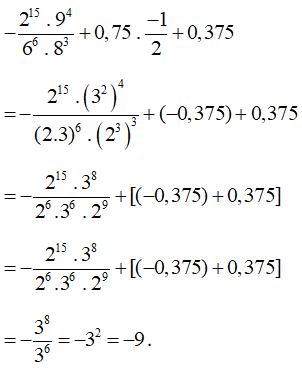
Bài 53 trang 26 Toán 7 Tập 1: Tìm số hữu tỉ x, biết:
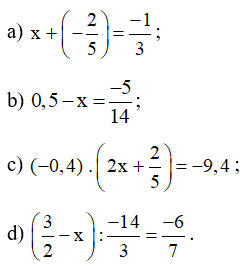
Lời giải:
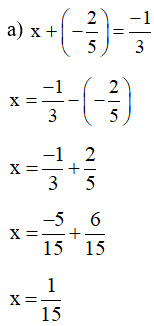
Vậy .
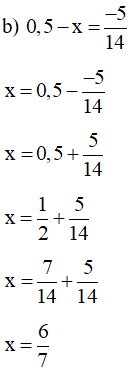
Vậy
c)
2x + 0,4 = 23,5
2x = 23,5 – 0,4
2x = 23,1
x = 11,55
Vậy x = 11,55
d)
1,5 – x = 4
x = 1,5 – 4
x = –2,5
Vậy x = –2,5.
Bài 54* trang 26 Toán 7 Tập 1:So sánh:
a) 224 và 216;
b) và ;
c) và .
Lời giải:
a) 224 và 216
Do 2 > 1 và 24 > 16 nên 224 > 216.
Vậy 224 và 216.
b) và
Ta có:
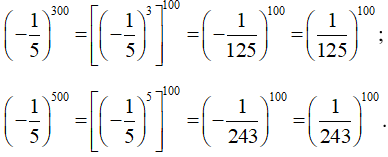
Do nên .
Vậy .
c) và .
Do nên .
Mặt khác nên .
Vậy .
Bài 55 trang 26 Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự tăng dần:
a) ;
b) (0,1)21; (−0,1)20; (0,1)22; (−0,1)19; 0.
Lời giải:
a) .
Ta thấy và 1 < 18 < 20 < 21 < 22.
Do đó .
Vậy các số được sắp xếp theo thứ tự tăng dần:
.
b) Ta có: (−0,1)19 < 0; (−0,1)20 = (0,1)20 > 0.
Ta thấy: 0 < 0,1 < 1 và 22 > 21 > 20
Suy ra (0,1)22 < (0,1)21 < (0,1)20 hay (0,1)22 < (0,1)21 < (−0,1)20
Do đó (−0,1)19 < 0 < (0,1)22 < (0,1)21 < (−0,1)20.
Vậy các số được sắp xếp theo thứ tự tăng dần:
(−0,1)19 < 0 < (0,1)22 < (0,1)21 < (−0,1)20.
(Nguồn: http://vnexpress.net/tac-hai-cua-viec-tre-cong-cap-di-hoc-4161875.html)
Bạn Đức học lớp 7 có cân nặng 46 kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp sách nặng 3,5 kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng kg để tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên?
Lời giải:
Theo khuyến nghị, khối lượng cặp sách bạn Đức nên mang không vượt quá là:
46 . 10% = 4,6 (kg).
Khối lượng bạn Đức có thể mang thêm nhiều nhất theo khuyến nghị là:
4,6 – 3,5 = 1,1 (kg).
Ta có: .
Do đó bạn Đức có thể mang theo nhiều nhất 6 quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 5: Biểu diễn thập phân của số hữu tỉ
Bài 1: Số vô tỉ. Căn bậc hai số học
Bài 3: Giá trị tuyệt đối của một số thực
Lý thuyết Toán 7 Chương 1: Số hữu tỉ
1. Số hữu tỉ
- Số hữu tỉ là số viết được dưới dạng phân số .
- Tập hợp các số hữu tỉ kí hiệu là ℚ.
Chú ý:
- Mỗi số nguyên là một số hữu tỉ.
- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.
2. Biểu diễn số hữu tỉ trên trục số
- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.
- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.
- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.
- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.
3. Số đối của một số hữu tỉ
- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc 0 được gọi là hai số đối nhau.
- Số đối của số hữu tỉ a, kí hiệu là –a.
- Số đối của số 0 là 0.
4. So sánh các số hữu tỉ
4.1 So sánh hai số hữu tỉ
Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.
- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a.
- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương
- Nếu a < b và b < c thì a < c.
4.2 Cách so sánh hai số hữu tỉ
+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.
+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.
4.3 Minh họa trên trục số
Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :
- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.
- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.
5. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế
5.1 Quy tắc cộng, trừ hai số hữu tỉ
- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.
5.2 Tính chất của phép cộng các số hữu tỉ
- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.
- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.
5.3 Quy tắc chuyển vế
Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:
x + y = z ⇒ x = z – y
x – y = z ⇒ x = z + y
6. Nhân, chia hai số hữu tỉ
6.1 Quy tắc nhân, chia hai số hữu tỉ
- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.
6.2 Tính chất của phép nhân các số hữu tỉ
Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.
Nhận xét:
- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là . Ta có
- Số nghịch đảo của số hữu tỉ là a.
- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì .
7. Phép tính lũy thừa với số mũ tự nhiên
- Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x: với
Số x được gọi là cơ số, n gọi là số mũ.
- Quy ước x1 = x.
Chú ý:
xn đọc là “x mũ n” hoặc “x lũy thừa n” hoặc “lũy thừa bậc n của x”.
x2 còn được gọi là “x bình phương” hay “bình phương của x”.
x3 còn gọi là “x lập phương” hay “lập phương của x”.
Chú ý: Để viết lũy thừa bậc n của phân số , ta phải viết trong dấu ngoặc ( ), tức là .
8. Tích và thương của hai lũy thừa cùng cơ số
- Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
xm . xn = xm+n .
- Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia :
xm : xn = xm – n
- Quy ước x0 = 1 (x ≠ 0).
9. Lũy thừa của một lũy thừa
Khi tính lũy thừa của một lũy thừa ta giữ nguyên cơ số và nhân hai số mũ:
.
10. Thứ tự thực hiện các phép tính
- Đối với biểu thức không có dấu ngoặc:
+ Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ bên trái sang phải.
+ Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.
+ Khi biểu thức có chứa các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
- Đối với biểu thức có chứa dấu ngoặc:
+ Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong ngoặc trước.
+ Khi các biểu thức có chứa các dấu ngoặc ( ), [ ]; { } thì thứ tự thực hiện phép tính như sau: ( ) → [ ] →{ }.
11. Quy tắc dấu ngoặc
- Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữa nguyên dấu của các số hạng bên trong dấu ngoặc.
a + (b + c) = a + b + c
a + (b – c) = a + b – c
- Khi bỏ dấu ngoặc có dấu “–” đằng trước, ta phải đổi dấu của các số hạng bên trong dấu ngoặc: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.
a – (b + c) = a – b – c
a – (b – c) = a – b + c
Nhận xét: Nếu đưa các số hạng vào trong dấu ngoặc có dấu “–” đằng trước thì phải đổi dấu các số hạng đó.
12. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn
- Các số thập phân chỉ gồm hữu hạn chữ số sau dấu “,” được gọi là số thập phân hữu hạn.
- Các số thập phân mà trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi mãi được gọi là số thập phân vô hạn tuần hoàn. Chữ số hoặc cụm chữ số lặp đi lặp lại mãi mãi đó được gọi là chu kì của số thập phân vô hạn tuần hoàn.
13. Biểu diễn thập phân của số hữu tỉ
- Mỗi số hữu tỉ đều viết được dưới dạng phân số . Thực hiện phép tính
a : b ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
- Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.