Với giải sách bài tập Toán 7 Ôn tập chương 4 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Ôn tập chương 4

Giải Toán 7 trang 71 Tập 1

A. Câu hỏi (trắc nghiệm)

Tìm câu trả lời đúng trong các đáp án đã cho.

Câu 1 trang 71 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng?

A. Mọi tam giác có ít nhất một góc tù.

B. Mọi tam giác có ít nhất hai góc nhọn.

C. Mọi tam giác cân có một góc bằng 60°.

D. Tam giác vuông cân có hai góc vuông.

Hướng dẫn giải

Đáp án đúng là: B.

+ Giả sử ta có tam giác có hai góc tù với $\widehat{A}>90°$, $\widehat{B}>90°$.

Suy ra $\widehat{A}+\widehat{B}>90°+90°=180°$

Mà tổng ba góc trong một tam giác bất kì luôn bằng 180°.

Do đó, một tam giác không thể có hai góc tù hay một tam giác không thể có ít nhất một góc tù. Vậy câu A sai.

+ Tam giác tù có một góc tù và hai góc nhọn, tam giác vuông có một góc vuông và hai góc nhọn, tam giác nhọn có ba góc nhọn. Vậy mọi tam giác có ít nhất hai góc nhọn. Do đó câu B đúng.

+ Tam giác cân không nhất thiết phải có một góc bằng 60°.

Chẳng hạn, tam giác ABC có $\widehat{A}=100°,\widehat{B}=\widehat{C}=40°$ thì tam giác ABC cân tại đỉnh A.

Vậy câu C sai.

+ Tam giác không thể có hai góc vuông vì không thỏa mãn định lí tổng ba góc trong tam giác. Vậy câu D sai.

Câu 2 trang 71 Toán 7 Tập 1: Trong các câu sau đây, câu nào sai?

A. Tổng số đo ba góc trong một tam giác bằng 180°.

B. Tổng số đo hai góc nhọn trong một tam giác vuông bằng 90°.

C. Tổng số đo hai góc nhọn trong một tam giác tù lớn hơn 90°.

D. Góc lớn nhất trong tam giác nhọn có số đo nhỏ hơn 90°.

Hướng dẫn giải

Đáp án đúng là: C

Câu A đúng theo định lí tổng ba góc trong tam giác.

Tam giác vuông có một góc vuông, do đó tổng của hai góc nhọn trong tam giác vuông bằng 180° – 90° = 90°. Vậy câu B đúng.

Vì trong tam giác tù có một góc tù, góc này lớn hơn 90°, vậy tổng hai góc nhọn trong tam giác tù phải nhỏ hơn 90° để thỏa mãn định lí tổng ba góc trong tam giác. Vậy câu C sai.

Tam giác nhọn có cả ba góc đều là góc nhọn, do đó góc lớn nhất trong tam giác nhọn có số đo nhỏ hơn 90°. Vậy câu D đúng.

Câu 3 trang 71 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng?

A. Hai tam giác có ba cặp góc tương ứng bằng nhau là hai tam giác bằng nhau.

B. Hai tam giác có ba cặp cạnh tương ứng bằng nhau là hai tam giác bằng nhau.

C. Hai tam giác có hai cặp cạnh tương ứng bằng nhau và một cặp góc tương ứng bằng nhau là hai tam giác bằng nhau.

D. Hai tam giác có một cặp cạnh tương ứng bằng nhau và cặp góc đối diện với cặp cạnh đó bằng nhau là hai tam giác bằng nhau.

Hướng dẫn giải

Đáp án đúng là: B

Câu A sai do ba cặp góc của tam giác tương ứng bằng nhau thì các cạnh tương ứng chưa chắc đã bằng nhau.

Câu B đúng theo trường hợp bằng nhau cạnh – cạnh – cạnh của hai tam giác.

Câu C sai, cặp góc tương ứng bằng nhau phải là góc xem giữa hai cạnh thì câu này mới đúng,

Câu D sai do ta mới chỉ có hai yếu tố.

Câu 4 trang 71 Toán 7 Tập 1: Trong các câu sau đây, câu nào sai?

A. Hai tam giác có cặp cạnh tương ứng bằng nhau và cặp góc xen giữa hai cặp cạnh đó bằng nhau thì hai tam giác bằng nhau.

B. Hai tam giác có một cặp cạnh tương ứng bằng nhau và hai cặp góc tương ứng cùng kề với cặp cạnh đó bằng nhau thì hai tam giác bằng nhau.

C. Hai tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau và các cặp góc tương ứng bằng nhau.

D. Hai tam giác có các cặp góc tương ứng bằng nhau thì các cặp cạnh tương ứng bằng nhau.

Hướng dẫn giải

Đáp án đúng là: D

Câu A đúng theo trường hợp bằng nhau cạnh – góc – cạnh của hai tam giác.

Câu B đúng theo trường hợp bằng nhau góc – cạnh – góc của hai tam giác.

Câu C đúng theo định nghĩa hai tam giác bằng nhau.

Câu D sai, do hai tam giác chưa chắc đã bằng nhau.

Câu 5 trang 71 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng?

A. Tam giác có ba cạnh bằng nhau là tam giác đều.

B. Tam giác có hai góc bằng nhau là tam giác đều.

C. Tam giác nhọn có hai cạnh bằng nhau là tam giác đều.

D. Tam giác vuông có một góc có số đo bằng 60° là tam giác đều.

Hướng dẫn giải

Đáp án đúng là: A

Theo định nghĩa, tam giác đều là tam giác có ba cạnh bằng nhau.

Trong tam giác đều, ba góc bằng nhau và bằng 60°.

Do đó câu A đúng và câu B, C, D sai.

Giải Toán 7 trang 72 Tập 1

Câu 6 trang 72 Toán 7 Tập 1: Trong các câu sau đây, câu nào sai?

A. Tam giác tù là tam giác có một góc có số đo lớn hơn 90°.

B. Tam giác vuông là tam giác có một góc có số đo bằng 90°.

C. Tam giác cân là tam giác có ba góc có số đo bằng 60°.

D. Tam giác nhọn là tam giác có ba góc có số đo nhỏ hơn 90°.

Hướng dẫn giải

Đáp án đúng là: C

Tam giác tù có một góc tù và góc tù thì có số đo lớn hơn 90°, do đó câu A đúng.

Tam giác vuông là tam giác có một góc vuông nên câu B đúng.

Tam giác nhọn là tam giác có cả ba góc đều là góc nhọn, số đo góc nhọn nhỏ hơn 90°.

Vậy câu D đúng.

Tam giác cân là tam giác có hai cạnh bằng nhau. Trong tam giác cân, hai góc ở đáy bằng nhau.

Vậy câu C sai.

Câu 7 trang 72 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng?

A. Đường thẳng đi qua trung điểm của đoạn thẳng AB là đường trung trực của đoạn thẳng AB.

B. Đường thẳng vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.

C. Tập hợp các điểm các đều hai điểm phân biệt A và B là đường thẳng đi qua trung điểm của đoạn thẳng AB.

D. Đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.

Hướng dẫn giải

Đáp án đúng là: D

Theo định nghĩa, đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Vậy câu D đúng.

B. Bài tập

Bài 4.51 trang 72 Toán 7 Tập 1: Tính số đo các góc x, y, z, t, v trong Hình 4.55.

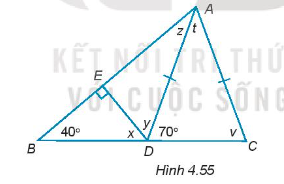
Hướng dẫn giải

Tam giác BED vuông tại E nên $\widehat{B}+\widehat{EDB}=90°hay\widehat{B}+x=90°$.

Suy ra $x=90°-\widehat{B}=$90° – 40° = 50°.

Ta có: $\widehat{ADB}+\widehat{ADC}=180°$ (hai góc kề bù)

$\Rightarrow \widehat{ABD}=180°-\widehat{ADC}$$=180°-70°=110°$.

Lại có: $\widehat{BDE}+\widehat{ECA}=\widehat{ABD}$ hay x + y = 110°.

Suy ra y = 110° – x = 110° – 50° = 60°.

Tam giác AED vuông tại E nên $\widehat{EDA}+\widehat{EAD}=90°$ hay y + z = 90°.

Suy ra z = 90° – y = 90° – 60° = 30°.

Tam giác ADC có AD = AC nên tam giác ADC cân tại đỉnh A.

Suy ra $\widehat{ACD}=\widehat{ADC}=70°$ hay v = 70°.

Áp dụng định lí tổng ba góc trong tam giác ADC, ta có:

$\widehat{ADC}+\widehat{ACD}+\widehat{CAD}=180°$

$\Rightarrow \widehat{CAD}=180°-\widehat{ACD}-\widehat{ADC}$$=180°-70°-70°=40°$ hay t = 40°.

Vậy x = 50°, y = 60°, z = 30°, v = 70°, t = 40°.

Bài 4.52 trang 72 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng, câu nào sai?

a) Tam giác nhọn có ba góc đều nhọn.

b) Tam giác vuông có đúng hai góc nhọn.

c) Tam giác tù có đúng một góc nhọn.

d) Trong ba góc của một tam giác tù, góc tù có số đo lớn nhất.

Hướng dẫn giải

Câu a đúng theo định nghĩa tam giác nhọn.

Tam giác vuông có một góc vuông và hai góc còn lại phải là góc nhọn để đảm bảo định lí tổng ba góc trong tam giác do đó câu b đúng.

Tam giác tù có một góc tù và hai góc còn lại là hai góc nhọn nên góc tù có số đo lớn nhất, do đó câu c sai và câu d đúng.

Vậy a), b), d) đúng và c) sai.

Bài 4.53 trang 72 Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng, câu nào sai?

a) Tam giác cân có một góc bằng 60° là tam giác đều.

b) Tam giác cân là tam giác nhọn.

c) Tổng hai góc nhọn của một tam giác vuông bằng 90°.

d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45°.

Hướng dẫn giải

a) Câu a) đúng.

Giải thích:

+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đáy  = 60°.

Khi đó, $\widehat{C}=\widehat{B}=60°$.

Theo định lí tổng ba góc trong tam giác, ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$.

$\Rightarrow \widehat{A}=180°-\widehat{B}-\widehat{C}$$=180°-60°-60°=60°$.

Do đó, $\widehat{A}=\widehat{B}=\widehat{C}=60°$, nên tam giác ABC cân tại đỉnh C.

Vậy tam giác ABC đều.

+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đỉnh $\widehat{A}=60°$.

Theo định lí tổng ba góc trong tam giác, ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$.

Mà $\widehat{B}=\widehat{C}$ (do tam giác ABC cân đỉnh A).

Do đó, $\widehat{B}+\widehat{B}=180°-\widehat{A}=$$180°-60°=120°$, suy ra $\widehat{B}=60°$.

Do đó, $\widehat{A}=\widehat{B}=\widehat{C}=60°$, nên tam giác ABC cân tại đỉnh C.

Vậy tam giác ABC đều.

b) Câu b) sai.

Chẳng hạn tam giác ABC cân tại đỉnh A có $\widehat{A}=100°$, $\widehat{B}=\widehat{C}=40°$, đây là tam giác tù.

c) Từ định lí tổng ba góc trong tam giác, ta suy ra tổng hai góc nhọn của một tam giác vuông bằng 90°.

Vậy câu c) đúng.

d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45° là câu đúng.

Giả sử có tam giác ABC vuông tại A, cân tại B, khi đó $\widehat{A}=\widehat{C}=90°$, do đó $\widehat{A}+\widehat{B}+\widehat{C}>180°$ không thỏa mãn định lí tổng ba góc trong tam giác.

Vậy tam giác vuông cân thì luôn cân tại đỉnh góc vuông và từ định lí tổng ba góc và tính chất của tam giác cân, ta tính được số đo hai góc nhọn bằng 45°.

Vậy câu a), c), d) đúng và câu b) sai.

Giải Toán 7 trang 73 Tập 1

Bài 4.54 trang 73 Toán 7 Tập 1: Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).

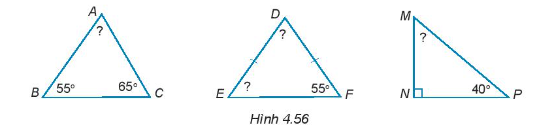
Hướng dẫn giải

+ Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$.

$\Rightarrow \widehat{A}=180°-\widehat{B}-\widehat{C}=$$180°-55°-65°=60°$.

+ Tam giác DEF có DE = DF, do đó tam giác DEF cân tại đỉnh D.

Suy ra $\widehat{E}=\widehat{F}=55°$.

Áp dụng định lí tổng ba góc trong tam giác DEF, ta có:

$\widehat{D}+\widehat{E}+\widehat{F}=180°$.

$\Rightarrow \widehat{D}=180°-\widehat{E}-$$\widehat{F}=180°-55°-55°=70°$.

+ Tam giác MNP vuông tại N, do đó $\widehat{M}+\widehat{P}=90°$.

Suy ra $\widehat{M}=90°-\widehat{P}=90°-40°=50°$.

Bài 4.55 trang 73 Toán 7 Tập 1: Cho các điểm A, B, C, D như Hình 4.57.

a) Chứng minh rằng $\widehat{DAC}=\widehat{DBC}$.

b) Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?

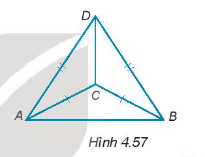
Hướng dẫn giải

a) Xét tam giác DAC và tam giác DBC có:

DA = DB (gt)

DC: cạnh chung

AC = BC (gt)

Do đó, ∆DAC = ∆DBC (c – c – c).

Suy ra $\widehat{DAC}=\widehat{DBC}$.

b) Ta có: DA = DB nên D cách đều A và B, do đó D thuộc đường trung trực của đoạn thẳng AB.

Tương tự CA = CB nên C cách đều A và B, do đó C thuộc đường trung trực của đoạn thẳng AB.

Vậy đường thẳng DC là đường trung trực của đoạn thẳng AB.

Do đó đường thẳng DC vuông góc với đường thẳng AB.

Bài 4.56 trang 73 Toán 7 Tập 1: Cho các điểm A, B, C, D, E, F như Hình 4.58.

a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

b) Chứng minh ∆ADE = ∆ADF.

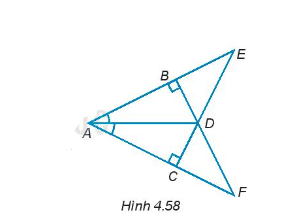
Hướng dẫn giải

a) Xét tam giác vuông ABD và tam giác vuông ACD có:

AD: cạnh chung

$\widehat{BAD}=\widehat{CAD}$ (gt)

Do đó, ∆ABD = ∆ACD (cạnh huyền – góc nhọn).

Xét tam giác vuông ABF và tam giác vuông ACE có:

AB = AC (do ∆ABD = ∆ACD)

$\widehat{FAB}=\widehat{EAC}$ (góc chung)

Do đó, ∆ABF = ∆ACE (cạnh góc vuông và góc nhọn kề).

Xét tam giác vuông BDE và tam giác vuông CDF có:

BD = CD (do ∆ABD = ∆ACD)

$\widehat{BDE}=\widehat{CDF}$ (hai góc đối đỉnh)

Do đó, ∆BDE = ∆CDF (cạnh góc vuông và góc nhọn kề).

Vậy ta có ba cặp tam giác vuông bằng nhau như trên.

b) Xét tam giác ADE và tam giác ADF có:

AE = AF (do ∆ABF = ∆ACE)

$\widehat{EAD}=\widehat{FAD}$ (gt)

AD: cạnh chung

Do đó, ∆ADE = ∆ADF (c – g – c).

Bài 4.57 trang 73 Toán 7 Tập 1: Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).

a) Chứng minh rằng MP = MQ và AP = AQ.

b) Đường thẳng PQ có vuông góc với AM không? Vì sao?

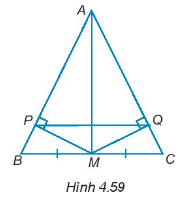
Hướng dẫn giải

a) Xét tam giác vuông PBM và tam giác vuông QCM có:

BM = MC (do M là trung điểm của BC)

$\widehat{B}=\widehat{C}$ (do tam giác ABC cân tại đỉnh A)

Do đó, ∆PBM = ∆QCM (cạnh huyền – góc nhọn).

Suy ra MP = MQ.

Ta lại có: AB = AC (do tam giác ABC cân tại đỉnh A).

AB = AP + PB, AC = AQ + QC.

Suy ra AP + PB = AQ + QC

Mà PB = QC (do ∆PBM = ∆QCM)

Do đó AP = AQ.

b) Theo câu a ta có, AP = AQ và MP = MQ, do đó A và M cùng cách đều hai điểm P, Q nên AM là đường trung trực của đoạn thẳng PQ.

Do đó, AM vuông góc với PQ.

Giải Toán 7 trang 74 Tập 1

Bài 4.58 trang 74 Toán 7 Tập 1: Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:

a) AP = BQ.

b) ∆APB = ∆BQA.

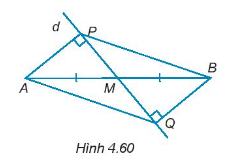
Hướng dẫn giải

a) Xét tam giác vuông PAM và tam giác vuông QBM có:

AM = BM (do M là trung điểm của AB)

$\widehat{PMA}=\widehat{QMB}$ (hai góc đối đỉnh)

Do đó, ∆PAM = ∆QBM (cạnh huyền – góc nhọn).

Suy ra AP = BQ.

b) Xét tam giác APB và tam giác BQA có:

AP = BQ (cmt)

$\widehat{PAB}=\widehat{QBA}$ (do ∆PAM = ∆QBM)

AB: cạnh chung

Do đó, ∆APB = ∆BQA (c – g – c).

Bài 4.59 trang 74 Toán 7 Tập 1: Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.

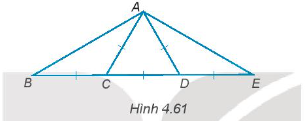
Hướng dẫn giải

Ta có: AD = AC = CD, do đó tam giác ACD là tam giác đều.

Suy ra $\widehat{ACD}=\widehat{ADC}=\widehat{CAD}=60°$.

Ta có: $\widehat{ACB}+\widehat{ACD}=180°$ (hai góc kề bù)

$\Rightarrow \widehat{ACB}=180°-\widehat{ACD}$$=180°-60°=120°$.

Tam giác ABC có CB = CA nên tam giác ACB cân tại đỉnh C.

Suy ra $\widehat{ABC}=\widehat{BAC}$.

Ta có: $\widehat{A\text{}BC}+\widehat{BAC}+\widehat{ACB}=180°$ (định lí tổng ba góc trong tam giác)

Do đó, $2\widehat{ABC}=180°-\widehat{ACB}=$$180°-120°=60°$.

Suy ra $\widehat{ABC}=\frac{60°}{2}=30°$.

Do đó, $\widehat{ABC}=\widehat{BAC}=30°$.

Chứng minh tương tự đối với tam giác ADE cân tại đỉnh D, ta cũng có: $\widehat{DEA}=\widehat{DAE}=30°$

Ta có:

$$\begin{gathered} \widehat{BAE}=\widehat{BAC}+\widehat{CAD}+\widehat{DAE} \\ =30°+60°+30°=120° \end{gathered}$$.

Vậy trong tam giác ABE có: $\widehat{ABE}=\widehat{ABC}=30°$; $\widehat{AEB}=\widehat{DEA}=30°$ và $\widehat{BAE}=120°$.

Bài 4.60 trang 74 Toán 7 Tập 1: Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.

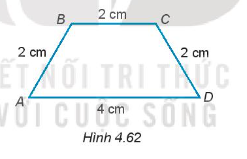
Hướng dẫn giải

Gọi O là trung điểm của AD.

Khi đó, AO = OD = $\frac{AD}{2}=\frac{4}{2}=2$ (cm).

Do đó, AB = BC = CD = AO = OD = 2 cm.

Tam giác ABO có AB = BO nên tam giác ABO cân tại đỉnh A.

Suy ra $\widehat{ABO}=\widehat{AOB}$.

Lại có: AD // BC (do ABCD là hình thang cân có AD và BC là đáy)

Suy ra $\widehat{CBO}=\widehat{AOB}$ (hai góc so le trong).

Do đó, $\widehat{ABO}=\widehat{AOB}=\widehat{CBO}$.

Xét tam giác ABO và tam giác CBO có:

AB = BC (= 2 cm)

$\widehat{ABO}=\widehat{CBO}$ (cmt)

BO: cạnh chung

Do đó, ∆ABO = ∆CBO (c – g – c).

Suy ra CO = AO = 2 cm.

Tam giác COD có CD = OD = OC (= 2 cm). Do đó tam giác COD là tam giác đều.

Suy ra $\widehat{D}=\widehat{CDO}=60°$.

Ta có: $\widehat{D}+\widehat{BCD}=180°$ (BC // AD, hai góc ở vị trí trong cùng phía)

Suy ra $\widehat{BCD\text{}}=180°-\widehat{D}$$=180°-60°=120°$.

Do ABCD là hình thang cân với AD và BC là đáy.

Vậy $\widehat{A}=\widehat{D}=60°$ và $\widehat{ABC}=\widehat{BCD}=120°$.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Ôn tập chương 4

Bài 17: Thu thập và phân loại dữ liệu

Bài 18: Biểu đồ hình quạt tròn

Bài 19: Biểu đồ đoạn thẳng

Lý thuyết Toán 7 Chương 4: Tam giác bằng nhau

1. Tổng các góc trong một tam giác

• Tổng ba góc trong một tam giác bằng 180°.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

• Phân loại tam giác dựa vào số đo góc:

+ Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

+ Tam giác có một góc tù được gọi là tam giác tù.

+ Tam giác có một góc vuông được gọi là tam giác vuông.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

2. Hai tam giác bằng nhau

• Hai tam giác bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

3. Các trường hợp bằng nhau của hai tam giác

• Trường hợp bằng nhau thứ nhất: cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

4. Các trường hợp bằng nhau của hai tam giác vuông

• Trường hợp: hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh góc vuông – góc nhọn kề

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

5. Tam giác cân

• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

• Tính chất:

+ Trong tam giác cân, hai góc ở đáy bằng nhau.

+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.

• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.

+ Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.

+ Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.

6. Đường trung trực của một đoạn thẳng

• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.