Với lời giải SBT Toán 7 trang 73 Tập 1 chi tiết trong Ôn tập chương 4 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Ôn tập chương 4

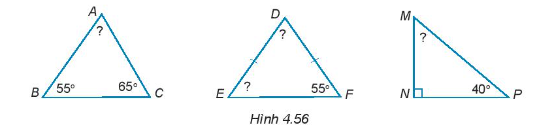
Bài 4.54 trang 73 SBT Toán 7 Tập 1: Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).

Hướng dẫn giải

+ Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$.

$\Rightarrow \widehat{A}=180°-\widehat{B}-\widehat{C}=$$180°-55°-65°=60°$.

+ Tam giác DEF có DE = DF, do đó tam giác DEF cân tại đỉnh D.

Suy ra $\widehat{E}=\widehat{F}=55°$.

Áp dụng định lí tổng ba góc trong tam giác DEF, ta có:

$\widehat{D}+\widehat{E}+\widehat{F}=180°$.

$\Rightarrow \widehat{D}=180°-\widehat{E}-$$\widehat{F}=180°-55°-55°=70°$.

+ Tam giác MNP vuông tại N, do đó $\widehat{M}+\widehat{P}=90°$.

Suy ra $\widehat{M}=90°-\widehat{P}=90°-40°=50°$.

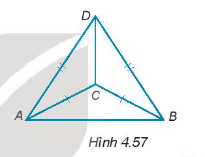
Bài 4.55 trang 73 SBT Toán 7 Tập 1: Cho các điểm A, B, C, D như Hình 4.57.

a) Chứng minh rằng $\widehat{DAC}=\widehat{DBC}$.

b) Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?

Hướng dẫn giải

a) Xét tam giác DAC và tam giác DBC có:

DA = DB (gt)

DC: cạnh chung

AC = BC (gt)

Do đó, ∆DAC = ∆DBC (c – c – c).

Suy ra $\widehat{DAC}=\widehat{DBC}$.

b) Ta có: DA = DB nên D cách đều A và B, do đó D thuộc đường trung trực của đoạn thẳng AB.

Tương tự CA = CB nên C cách đều A và B, do đó C thuộc đường trung trực của đoạn thẳng AB.

Vậy đường thẳng DC là đường trung trực của đoạn thẳng AB.

Do đó đường thẳng DC vuông góc với đường thẳng AB.

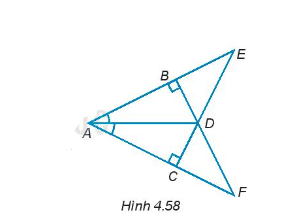
Bài 4.56 trang 73 SBT Toán 7 Tập 1: Cho các điểm A, B, C, D, E, F như Hình 4.58.

a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

b) Chứng minh ∆ADE = ∆ADF.

Hướng dẫn giải

a) Xét tam giác vuông ABD và tam giác vuông ACD có:

AD: cạnh chung

$\widehat{BAD}=\widehat{CAD}$ (gt)

Do đó, ∆ABD = ∆ACD (cạnh huyền – góc nhọn).

Xét tam giác vuông ABF và tam giác vuông ACE có:

AB = AC (do ∆ABD = ∆ACD)

$\widehat{FAB}=\widehat{EAC}$ (góc chung)

Do đó, ∆ABF = ∆ACE (cạnh góc vuông và góc nhọn kề).

Xét tam giác vuông BDE và tam giác vuông CDF có:

BD = CD (do ∆ABD = ∆ACD)

$\widehat{BDE}=\widehat{CDF}$ (hai góc đối đỉnh)

Do đó, ∆BDE = ∆CDF (cạnh góc vuông và góc nhọn kề).

Vậy ta có ba cặp tam giác vuông bằng nhau như trên.

b) Xét tam giác ADE và tam giác ADF có:

AE = AF (do ∆ABF = ∆ACE)

$\widehat{EAD}=\widehat{FAD}$ (gt)

AD: cạnh chung

Do đó, ∆ADE = ∆ADF (c – g – c).

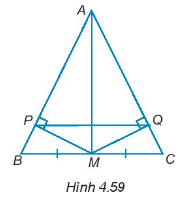
Bài 4.57 trang 73 SBT Toán 7 Tập 1: Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).

a) Chứng minh rằng MP = MQ và AP = AQ.

b) Đường thẳng PQ có vuông góc với AM không? Vì sao?

Hướng dẫn giải

a) Xét tam giác vuông PBM và tam giác vuông QCM có:

BM = MC (do M là trung điểm của BC)

$\widehat{B}=\widehat{C}$ (do tam giác ABC cân tại đỉnh A)

Do đó, ∆PBM = ∆QCM (cạnh huyền – góc nhọn).

Suy ra MP = MQ.

Ta lại có: AB = AC (do tam giác ABC cân tại đỉnh A).

AB = AP + PB, AC = AQ + QC.

Suy ra AP + PB = AQ + QC

Mà PB = QC (do ∆PBM = ∆QCM)

Do đó AP = AQ.

b) Theo câu a ta có, AP = AQ và MP = MQ, do đó A và M cùng cách đều hai điểm P, Q nên AM là đường trung trực của đoạn thẳng PQ.

Do đó, AM vuông góc với PQ.

Xem thêm các bài giải sách bài tập Toán 7 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 7 trang 71 Tập 1

Giải SBT Toán 7 trang 72 Tập 1

Giải SBT Toán 7 trang 74 Tập 1