Giải SGK Toán 7 (Kết nối tri thức) Bài tập cuối chương 4

Nguyễn Linh Anh Ngày: 26-08-2024 Lớp 7

6.3 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 4 chi tiết sách Toán 7 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 4

Video bài giảng Bài tập cuối chương 4 - Kết nối tri thức

Giải Toán 7 trang 87 Tập 1

Bài 4.33 trang 87 Toán lớp 7: Tính các số đo x, y trong tam giác dưới đây (H.4.75)

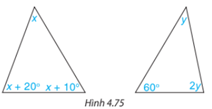
Phương pháp giải:

Áp dụng tổng 3 góc của 1 tam giác bằng 180 độ.

Lời giải:

Áp dụng định lí tổng ba góc trong tam giác,

+) Ta có:

$\begin{array}{l} x + x + 20^{o} + x + 10^{o} = 180^{o} \\ \Rightarrow 3 x = 150^{o} \\ \Rightarrow x = 50^{o} \end{array}$

+) Ta có:

$\begin{array}{l} y + 60^{o} + 2 y = 180^{o} \\ \Rightarrow 3 y = 120^{o} \\ \Rightarrow y = 40^{o} \end{array}$

Bài 4.34 trang 87 Toán lớp 7: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\hat{M A N} = \hat{M B N}$ .

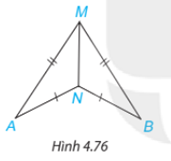
Phương pháp giải:

Chứng minh 2 tam giác MNA và MNB bằng nhau từ đó suy ra 2 góc tương ứng bằng nhau.

Lời giải:

Xét 2 tam giác MNA và MNB có:

AM=BM

AN=BN

MN chung

=> $Δ M N A = Δ M N B$ (c.c.c)

=> $\hat{M A N} = \hat{M B N}$ (2 góc tương ứng)

Bài 4.35 trang 87 Toán lớp 7: Trong Hình 4.77, có AO = BO,

\hat{O A M} = \hat{O B N}

. Chứng minh rằng AM = BN.

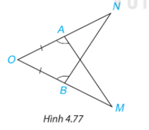
Phương pháp giải:

Chứng minh 2 tam giác OAM và OBN bằng nhau từ đó suy ra AM=BN.

Lời giải:

Xét 2 tam giác OAM và OBN có:

AO=BO

Góc O chung

=>(g.c.g)

=>AM=BN (2 cạnh tương ứng)

Bài 4.36 trang 87 Toán lớp 7: Trong Hình 4.78, ta có AN = BM, $\hat{B A N} = \hat{A B M}$ . Chứng minh rằng $\hat{B A M} = \hat{A B N}$ .

Phương pháp giải:

Chứng minh 2 tam giác ANB và BMA bằng nhau từ đó suy ra

\hat{B A M} = \hat{A B N}

Lời giải:

Xét hai tam giác BAM và ABN có:

AN=BM

$\hat{B A N} = \hat{A B M}$

AB chung

=> $Δ B A M = Δ A B N$ (c.g.c)

Vậy $\hat{B A M} = \hat{A B N}$ (2 góc tương ứng).

Bài 4.37 trang 87 Toán lớp 7: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.

Lời giải:

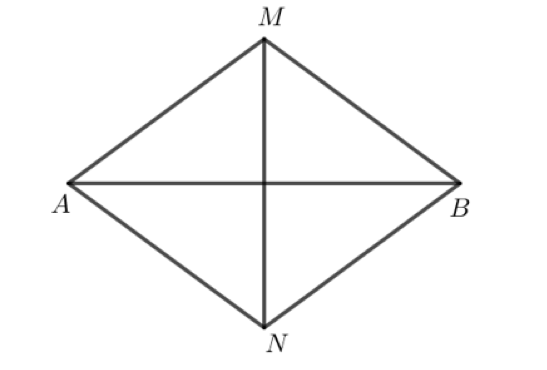
Toán lớp 7 Bài tập cuối chương 4 | Kết nối tri thức (ảnh 1)

Do M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB.

Do N nằm trên đường trung trực của đoạn thẳng AB nên NA = NB.

Mà MA = NA (theo giải thiết có AM = AN) nên MA = MB = NA = NB.

Suy ra MB = NB.

Xét tam giác AMB và tam giác ANB có:

MA = NA (giả thiết)

MB = NB (chứng minh trên)

AB: cạnh chung

Do đó, ∆AMB = ∆ANB (c – c – c).

Suy ra $\hat{AMB} = \hat{ANB}$ (hai góc tương ứng).

Vậy MB = NB và $\hat{AMB} = \hat{ANB}$

Bài 4.38 trang 87 Toán lớp 7: Cho tam giác ABC cân tại A có $\hat{A} = 120^{\circ}$ . Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) $Δ$ BAM = $Δ$ CAN;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Phương pháp giải:

a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g

b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau

Lời giải:

a) Xét 2 tam giác vuông BAM và CAN có:

AB=AC(Do tam giác ABC cân tại A)

$\hat{B} = \hat{C}$ (Do tam giác ABC cân tại A)

=> $Δ B A M = Δ C A N$ (g.c.g)

Xét tam giác ABC cân tại A, có $\hat{A} = 120^{\circ}$ có:

$\hat{B} = \hat{C} = \frac{180^{o} - 120^{o}}{2} = 30^{o}$ .

Xét tam giác ABM vuông tại A có:

$\begin{array}{l} \hat{B} + \hat{B A M} + \hat{A M B} = 180^{o} \\ \Rightarrow 30^{o} + 90^{o} + \hat{A M B} = 180^{o} \\ \Rightarrow \hat{A M B} = 60^{o} \\ \Rightarrow \hat{A M C} = 180^{o} - \hat{A M B} = 180^{o} - 60^{o} = 120^{o} \end{array}$

Xét tam giác MAC có:

$\begin{array}{l} \hat{A M C} + \hat{M A C} + \hat{C} = 180^{o} \\ \Rightarrow 120^{o} + \hat{M A C} + 30^{o} = 180^{o} \\ \Rightarrow \hat{M A C} = 30^{o} = \hat{C} \end{array}$

$\Rightarrow$ Tam giác AMC cân tại M.

Vì $Δ B A M = Δ C A N$ =>BM=CN => BN=MC

Xét 2 tam giác ANB và AMC có:

AB=AC

$A N = A M$ (do $Δ B A M = Δ C A N$ )

BN=MC

=> $Δ A N B = Δ A M C$ (c.c.c)

Mà tam giác AMC cân tại M.

=> Tam giác ANB cân tại N.

Bài 4.39 trang 87 Toán lớp 7: Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho $\hat{C A M} = 30^{o}$ . Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Phương pháp giải:

a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.

b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ

c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều

Lời giải:

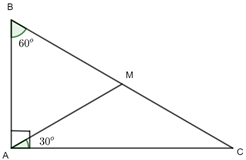
a) Xét tam giác ABC có:

$\begin{array}{l} \hat{A} + \hat{B} + \hat{C} = 180^{o} \\ => 90^{o} + 60^{o} + \hat{C} = 180^{o} \\ => \hat{C} = 30^{o} \end{array}$

Xét tam giác CAM có $\hat{A} = \hat{C} = 30^{o}$

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

$\begin{array}{l} \hat{C} + \hat{C M A} + \hat{C A M} = 180^{o} \\ => 30^{o} + \hat{C M A} + 30^{o} = 180^{o} \\ => \hat{C M A} = 120^{o} \\ => \hat{B M A} = 180^{o} - \hat{C M A} = 180^{o} - 120^{o} = 60^{o} \end{array}$

Xét tam giác ABM có:

$\begin{array}{l} \hat{B} + \hat{B M A} + \hat{B A M} = 180^{o} \\ => 60^{o} + 60^{o} + \hat{B A M} = 180^{o} \\ => \hat{B A M} = 60^{o} \end{array}$

Do $\hat{B A M} = \hat{B M A} = \hat{A B M} = 60^{o}$ nên tam giác ABM đều.

c) Do tam giác CAM cân tại M nên MA = MC (1).

Do tam giác BAM là tam giác đều nên MA = MB (2).

Từ (1) và (2) ta có MB = MC.

Mà M nằm giữa B và C nên M là trung điểm của BC.

Vậy M là trung điểm của BC.

Lý thuyết Toán 7 Chương 4: Tam giác bằng nhau

1. Tổng các góc trong một tam giác

• Tổng ba góc trong một tam giác bằng 180°.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

• Phân loại tam giác dựa vào số đo góc:

+ Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

+ Tam giác có một góc tù được gọi là tam giác tù.

+ Tam giác có một góc vuông được gọi là tam giác vuông.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

2. Hai tam giác bằng nhau

• Hai tam giác bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

3. Các trường hợp bằng nhau của hai tam giác

• Trường hợp bằng nhau thứ nhất: cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

4. Các trường hợp bằng nhau của hai tam giác vuông

• Trường hợp: hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh góc vuông – góc nhọn kề

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

5. Tam giác cân

• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

• Tính chất:

+ Trong tam giác cân, hai góc ở đáy bằng nhau.

+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.

• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.

+ Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.

+ Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.

6. Đường trung trực của một đoạn thẳng

• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.