Công thức tính khối lượng vật được giải phóng hay nhất

Lê Thị Thúy Hằng Ngày: 18-08-2023 Tổng hợp kiến thức

428

Với Công thức tính khối lượng vật được giải phóng Vật lý lớp 11 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức tính khối lượng vật được giải phóng từ đó biết cách làm bài tập Vật lý 11. Mời các bạn đón xem:

Công thức tính khối lượng vật được giải phóng - Vật lý lớp 11

1. Định nghĩa

Hiện tượng dương cực tan xảy ra khi các anion đi tới anôt kéo các ion kim loại của điện cực vào trong dung dịch.

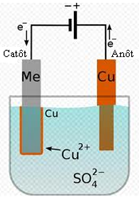
Ví dụ: Xét trường hơp bình điện phân đựng dung dịch CuSO₄ với cực dương bằng đồng:

Khi có dòng điện chạy qua, cation Cu²⁺ chạy về catôt và nhận electron trở thành nguyên tử Cu bám vào điện cực.

Cu²⁺ + 2e^- ® Cu

Ở anôt, electron bị kéo về cực dương của nguồn điện, tạo điều kiện hình thành ion Cu2+ trên bề mặt tiếp xúc với dung dịch.

Cu ® Cu²⁺ + 2e^-

Khi anion (SO₄)2- chạy về anôt, nó kéo ion Cu²⁺ vào dung dịch. Như vậy, đồng ở anôt sẽ tan dần vào trong dung dịch. Đó là hiện tượng dương cực tan.

Công thức tính khối lượng vật được giải phóng hay nhất - Vật lý lớp 11 (ảnh 1)

Khi xảy ra hiện tượng dương cực tan, dòng điện trong chất điện phân tải điện lượng cùng với vật chất (theo nghĩa hẹp) nên khối lượng chất giải phóng ở điện cực:

+ Tỉ lệ thuận với điện lượng chạy qua bình điện phân;

+ Tỉ lệ thuận với khối lượng của ion (hay khối lượng mol nguyên tử A của nguyên tố tạo nên ion ấy);

+ Tỉ lệ nghịch với điện tích của ion (hay hóa trị n của nguyên tố tạo ra ion ấy)

2. Công thức – đơn vị đo

Khối lượng vật chất được giải phóng ở điện cực của bình điện phân tỉ lệ thuận với điện lượng chạy qua bình đó.

m = k.q

Trong đó:

+ k gọi là đương lượng điện hoá của chất được giải phóng ở điện cực;

+ q là điện lượng chạy qua bình điện phân, có đơn vị Culong;

+ m là khối lượng vật chất được giải phóng ở điện cực của bình điện phân, có đơn vị gam (g).

Đương lượng điện hoá k của một nguyên tố được xác định bởi công thức:

k = $\frac{1}{F} . \frac{A}{n}$

Trong đó:

+ k là đương lượng điện hóa;

+ F là số Fa-ra-đây, F = 96494 C/mol, thường lấy chắn là F = 96500 C/mol;

+ A là khối lượng mol nguyên tử của nguyên tố tạo nên ion, có đơn vị gam;

+ n là hóa trị của nguyên tố tạo ra ion.

Kết hợp hai định công thức trên, ta được công thức Fa-ra-đây xác định chất giải phóng ở điện cực:

m = $\frac{1}{F} . \frac{A}{n}$ It

Trong đó:

+ m là chất được giải phóng ở điện cực, tính bằng gam;

+ F là số Fa-ra-đây, F = 96494 C/mol, thường lấy chắn là F = 96500 C/mol;

+ A là khối lượng mol nguyên tử của nguyên tố tạo nên ion, có đơn vị gam;

+ n là hóa trị của nguyên tố tạo ra ion;

+ I là cường độ dòng điện chạy qua bình điện phân, có đơn vị ampe (A);

+ t là thời gian dòng điện chạy qua bình điện phân, có đơn vị giây (s).

3. Mở rộng

Khối lượng vật chất giải phóng ở điện cực dương cũng bằng khối lượng vật chất bám vào cực âm. Nên nhiều bài toán không hỏi khối lượng chất giải phóng ở điện cực mà hỏi khối lượng chất bám vào điện cực âm (catot) thì ta cũng sử dụng công thức m = k.q hoặc m = $\frac{1}{F} . \frac{A}{n}$ It.

Khi biết khối lượng chất được giải phóng và điện lượng qua bình điện phân có thể xác định đương lượng điện hóa k như sau:

$k = \frac{m}{q}$

Trong đó:

+ k gọi là đương lượng điện hoá của chất được giải phóng ở điện cực, có đơn vị g/C;

+ q là điện lượng chạy qua bình điện phân, có đơn vị Culong;

+ m là khối lượng vật chất được giải phóng ở điện cực của bình điện phân, có đơn vị gam (g).

Trong thực tế, hiện tượng dương cực tan được sử dụng trong mạ điện hoặc bóc một lớp mạ trên bề mặt vật có bề dày d, diện tích mạ S và khối lượng riêng của chất cần mạ là D. Ta tính được khối lượng lớp mạ là: m = D.V = D.S.d.

Trong đó:

+ D là khối lượng riêng của chất mạ, có đơn vị kg/m³ hoặc g/cm³;

+ V là thể tích lớp mạ; V = d.S, có đơn vị m²;

+ d là bề dày lớp mạ, có đơn vị m;

+ S là diện tích lớp mạ, có đơn vị m².

Từ công thức định luật Fa-ra-đây, ta có thể suy ra các đại lượng cường độ dòng điện, thời gian điện phân, khối lượng mol nguyên tử (từ đó xác định tên nguyên tố).

m = $\frac{1}{F} . \frac{A}{n}$ It => $I = \frac{m . F . n}{A . t}$

m = $\frac{1}{F} . \frac{A}{n}$ It => $t = \frac{m . F . n}{A . I}$

m = $\frac{1}{F} . \frac{A}{n}$ It => $A = \frac{m . F . n}{I . t} = \frac{m . F . n}{q}$

4. Bài tập ví dụ

Bài 1: Chiều dày của lớp Niken phủ lên một tấm kim loại là d = 0,1 mm sau khi điện phân trong 30 phút. Diện tích mặt phủ của tấm kim loại là 30 cm². Cho biết Niken có khối lượng riêng là D = 8,9.10³ kg/m³, nguyên tử khối A = 58 và hoá trị n = 2. Cường độ dòng điện qua bình điện phân là bao nhiêu?

Bài giải:

Khối lượng lớp mạ là:

m = D.S.d = 8,9.10³. 30.10^-4 . 0,1.10^-3 = 26,7.10^-4 (kg) = 2,67 (g)

Áp dụng định luật Faraday:

m = $\frac{1}{F} . \frac{A}{n}$ It => $I = \frac{m . F . n}{A . t}$

$= \frac{2,67.96500.2}{58.30.60} = {4,94}_{} (A)$

Đáp án: I = 4,94 A

Bài 2: Một bình điện phân đựng dung dịch bạc nitrat với anốt bằng bạc. Điện trở của bình điện phân là R = 2 W. Hiệu điện thế đặt vào hai cực là U = 10 V. Cho A = 108 và n = 1. Khối lượng bạc giải phóng ở cực dương sau 2 giờ là bao nhiêu?

Bài giải:

Cường độ dòng điện chạy qua bình điện phân là:

$I = \frac{U}{R} = \frac{10}{2} = 5_{} (A)$

Khối lượng bạc giải phóng ở cực dương sau 2 giờ là:

m = $\frac{1}{F} . \frac{A}{n}$ It = $\frac{1}{96500} . \frac{108}{1} .5.2.3600 = {40,3}_{} (g)$