Với giải sách bài tập Toán 7 Ôn tập chương 2 trang 33, 34 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Ôn tập chương 2 trang 33, 34
A. Câu hỏi (trắc nghiệm)
Tìm câu trả lời đúng trong các đáp án đã cho:
Giải SBT Toán 7 trang 33 Tập 1
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: C
Ta có:
là phân số tối giản và có mẫu số là 512. Ta có 512 = 29 nên có thể viết được dưới dạng số thập phân hữu hạn.
. Ta thấy có mẫu số là 16 mà 16 = 24 nên có thể viết được dưới dạng số thập phân hữu hạn hay có thể viết dưới dạng số thập phân hữu hạn.
đây là phân số tối giản có mẫu số là 528. Ta có 528 = 24.3.11 nên viết được dưới dạng số thập phân vô hạn tuần hoàn.
đây là phân số tối giản có mẫu số là 512 = 29 nên có thể viết được dưới dạng số thập phân hữu hạn.
Câu hỏi 2 trang 33 sách bài tập Toán lớp 7 Tập 1:Số 3,(5) viết được thành phân số nào sau đây?
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là B
3,(5) = 3 + 0,(5) = 3 + 5.0,(1) = 3 + 5. = 3 + = .
Câu hỏi 3 trang 33 sách bài tập Toán lớp 7 Tập 1:Số nào dưới đây là bình phương của một số hữu tỉ?
A. 17;
B. 153;
C. 15,21;
D. 0,10100100010000…(viết liên tiếp sau dấu phẩy các lũy thừa của 10: 1010010001000…)
Lời giải:
Đáp án đúng là C
Ta đã biết, căn bậc hai số học của các số tự nhiên không chính phương đều là số vô tỉ nên 17 không phải là bình phương của một số hữu tỉ.
Mặt khác vì 153 = 17.9 nên nếu 153 là bình phương của số hữu tỉ x thì 17.9 = x2, nên 17 = suy ra 17 là bình phương của số hữu tỉ (vô lí).
Do đó, A và B đều sai. Mặt khác, nếu 0,101001000… là bình phương của số hữu tỉ thì 0,101001000… = . Suy ra 0,101001000.. là số thập phân vô hạn tuần oàn, điều này là vô lí. Do đó, D sai nên chỉ còn C đúng.
Ta sẽ thấy 15,21 = 3,92.
Câu hỏi 4 trang 33 sách bài tập Toán lớp 7 Tập 1:Giá trị nhỏ nhất của biểu thức là:
A. -4
B. 8
C. 0
D. -8
Lời giải:
Đáp án đúng là: A
Vì x2 ≥ 0 nên x2 +16 ≥ 0 + 16 = 16, do đó,
nên 4 - 8 = -4.
Vậy giá trị nhỏ nhất của biểu thức là -4. Dấu “=” xảy ra khi x = 0.
Câu hỏi 5 trang 33 sách bài tập Toán lớp 7 Tập 1:Giá trị lớn nhất của biểu thức là:
A. -2;
B. ;
C. 2;
D. .
Lời giải:
Đáp án đúng là: C
Để căn xác định thì x ≥ 5
Với mọi x ≥ 5 thì nên
Do đó, nên hay
Vậy giá trị lớn nhất của biểu thức là 2 đạt được khi x = 5.
Câu hỏi 6 trang 33 sách bài tập Toán lớp 7 Tập 1:Trong các khẳng định sau, khẳng định nào đúng?
A. Tích của hai số vô tỉ là một số vô tỉ;
B. Tổng của hai số vô tỉ là một số vô tỉ;
C. Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ;
D. Thương của hai số vô tỉ là một số vô tỉ.
Lời giải:
Đáp án đúng là C
A. Tích của hai số vô tỉ là một số vô tỉ;
Khảng định này sai vì là số vô tỉ nhưng tích của . = 2 là số hữu tỉ.
B. Tổng của hai số vô tỉ là một số vô tỉ;
Khẳng định này sai vì là số vô tỉ và - cũng là số vô tỉ nhưng + (-) = 0 lại là số hữu tỉ.
C. Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ;
Khẳng định này đúng vì tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ.
D. Thương của hai số vô tỉ là một số vô tỉ.
Khẳng định này sai vì là số vô tỉ nhưng : = 1 lại là số hữu tỉ.
Câu hỏi 7 trang 33 sách bài tập Toán lớp 7 Tập 1:Với mọi số thực x. Khẳng định nào sau đây sai?
A. |x| ≥ x;
B. |x| ≥ -x;
C. |x|2 = x2;
D. |x| = x.
Lời giải:
Đáp án đúng là: D
Khẳng định sai là D vì nếu x < 0 thì |x| = -x.
Ví dụ: |-5| = 5.
A. |x – y| = x – y;
B. | x – y| = |x| – |y|;
C. |x + y| = |x| + |y|;
D. |x + y| = |x| – |y| nếu x > 0 > y và |x| ≥ |y|.
Lời giải:
Đáp án đúng là: D
A sai , khi x < y
B sai nếu x = 0 và y khác 0
C sai, chẳng hạn khi x = -y và y khác 0
D đúng, theo quy tắc cộng hai số trái dấu.
B. Bài tập
Giải SBT Toán 7 trang 34 Tập 1
6,238.3,91 = 21,390558.
Lời giải:
Làm tròn số 6,238 đến hàng đơn vị ta thu được kết quả là 6. Làm tròn 3,91 đến hàng đơn vị ta thu được kết quả là 4.
Ta có 6,238.3,91 ≈ 6.4 = 24. Nên kết quả của phép tính 6,238.3,91 sẽ gần với 24.
Mà kết quả đề bài cho là 21,390558 rất xa so với 24 nên phép tính sai.
Lời giải:
Làm tròn số 1,(8) tới hàng đơn vị ta thu được kết quả là 2.
Ta có: 28,1 . 1,(8) ≈ 28,1 . 2 = 56,2. Vậy kết qảu của phép tính phải gần với 56,2 nhưng kết quả đề bài cho lại là 55,0(7) khác xa 56,2. Nên kết quả phép tính đề bài sai.
Bài 2.39 trang 34 sách bài tập Toán lớp 7 Tập 1: Chứng tỏ rằng 0,(3)2 = 0, (1).
Lời giải:
Ta có: 0,(3) = 3. 0,(1) = 3. = .
Do đó, 0,(3)2 = .
Do đó, 0,(3)2 = 0,(1).
Bài 2.40 trang 34 sách bài tập Toán lớp 7 Tập 1: Viết số 0,1(235) dưới dạng phân số.
Lời giải:
Ta có: 0,1(235) = 1, (235) : 10 = (1 + 0,(235)) : 10
Đặt x = 0,(235) thì 1000x = 235,(235) = 235 + x, suy ra 999x = 23 nên x = .
Do đó, 0,1(235) = .
Lời giải:
2,25 – 2,(3) = (2 + 0,25) – (2 + 0,(3)) = 2 + 0,25 – 2 – 0,(3) = 0,25 – 0,(3)
Ta có: 0,25 = ; 0,(3) = 3. 0,(1)
Do đó, 2,25 – 2, (3) = = –0,08(3)
Ta làm tròn kết quả đến hàng phần nghìn thu được kết quả làm tròn là -0,083.
Bài 2.42 trang 34 sách bài tập Toán lớp 7 Tập 1: So sánh a = 1,0(10) và b = 1,(01).
Lời giải:
Vì hai số đều có phần nguyên là 1 giống nhau nên ta đi so sánh phần thập phân của hai số là 0,0(10) và 0,(01).
Đặt x = 0,0(10) và y = 0,(01).
Ta thấy 1000x = 10,(10) = 10 + 0,(10) = 10 + 10x nên 990x = 10. Suy ra x =
Tương tự, 100y = 1,(01) = 1 + y nên 99y = 1. Suy ra y = .
Do đó, x = y = .
Suy ra, a = b.
Lời giải:
Số a = 555 555 có tổng các chữ số bằng 30 và 30 chia 9 dư 3 nên a chia 9 dư 3. Nếu là số hữu tỉ thì a phải là số chính phương, tức là a = n2 . Các số chính phương đầu tiên là 0; 4; 9; 16;25; 36;49;64; 81; 100; 121; 144; 169… Khi ta chia các số này cho 9 ta thấy các số dư lần lượt là 0; 4; 0; 7; 7; 1; 0; 4; 0; 7;… Các số dư tuần hoàn với chu kỳ là 0; 4; 0; 7; 7; 1. Như vậy các số chính phương khi chia cho 9 không bao giờ có dư 3. Từ đó, a= 555 555 không phải số chính phương nên là số vô tỉ.
Lời giải:
Ta có 11…1 có 101 chữ số 1 nên tổng các chữ số của nó bằng 101.
Vì 101 chia cho 3 dư 2 nên 11...1 (101 số 1) chia cho 3 cũng dư 2.
Mặt khác, bình phương của một số tự nhiên chỉ có thể chia hết cho 3 hoặc chia 3 dư 1 nên 11…1 (101 chữ số 1) không phải số chính phương. Vì vậy là số vô tỉ.
Lời giải:
+) Nếu x, y ≥ 0 thì xy ≥ 0 và x = |x| = a; y = |y| = b; |xy| = xy = ab.
Do đó, |xy| = ab.
+) Nếu x, y < 0 thì xy > 0 và x = -|x| = -a; y = -|y| = -b ; |xy| = (-a).(-b) = ab.
Do đó, |xy| = ab.
+) Nếu x, y trái dấu, ví dụ x > 0 và y < 0 thì x.y < 0
Nên |xy| = -xy = (-a).(-b) = ab.
Lời giải:
Ta có: |x – 1| + | x – 3| = |x – 1| + |3 – x| ≥ |(x – 1) + (3 – x)| = |x – 1 + 3 – x| = |2| = 2
Vì |x – 1| + | x – 3| = |x – 1| + |3 – x| ≥ 2 mà 2 > nên không có số thực nào thỏa mãn |x – 1| + |x – 3| = .
Lời giải:
Ta có: |x | + |x – 4| = |x| + |4 – x| ≥ | x + (4 – x)| = |x + 4 – x| = |4|
Lại có: |x – 2| ≥ 0 nên |x| + |x – 2| + |x – 4| ≥ 4 (điều phải chứng minh).
Lời giải:
Giả sử x là một số vô tỉ và n là một số nguyên dương. Nếu tích nx là số hữu tỉ thì x = là số hữu tỉ (thương của hai số hữu tỉ là một số hữu tỉ), trái với giả thiết x là số vô tỉ. Vậy nx phải là số vô tỉ.
Như vậy, đều là số vô tỉ, do đó có vô số số vô tỉ.
a) Tổng của hai số vô tỉ là một số vô tỉ.
b) Tổng của hai số vô tỉ dương là một số vô tỉ.
c) Tổng của hai số vô tỉ âm là một số vô tỉ.
Lời giải:
a) Tổng của hai số vô tỉ là một số vô tỉ.
Kết luận này sai vì là số vô tỉ và - nhưng + (-) = 0 là số hữu tỉ.
b) Tổng của hai số vô tỉ dương là một số vô tỉ.
Khẳng định này sai vì và 5 - là các số vô tỉ dương nhưng tổng của chúng + (5 - ) = + 5 - = 5 là một số hữu tỉ
c) Tổng của hai số vô tỉ âm là một số vô tỉ.
Khảng định này sai vì - và -5 + là các số vô tỉ âm nhưng (-) + (-5 + ) = - + (-5) + = -5 là một số hữu tỉ.
Lời giải:
Chia hình vuông đã cho thành 25 hình vuông nhỏ có cạnh bằng 1. Nếu trong mỗi hình vuông nhỏ có không quá ba điểm (trong số các điểm đã cho) thì trong hình vuông lớn có không quá 25.3 = 75 (điểm), trái với giả thiết trong hình vuông lớn có 76 điểm. Như vậy, có ít nhất một hình vuông nhỏ (cạnh bằng 1) chưa bốn điểm (trong các điểm đã cho). Hình tròn với đường kính là đường chéo của hình vuông nhỏ này chứa toàn bộ hình vuông nhỏ và có bán kính .
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Lý thuyết Chương 2: Số thực
1. Số thập phân vô hạn tuần hoàn
• Số thập phân vô hạn tuần hoàn là biểu diễn thập phân của một số có phần thập phân lặp lại (lặp lại giá trị của nó ở các khoảng đều đặn) và phần lặp lại vô hạn không phải là số không.
• Chu kì của số thập phân vô hạn tuần hoàn là phần được lặp lại vô hạn lần.
• Số thập phân hữu hạn là số thập phân như 0,34; 1,2; 6,7; …
Ví dụ:
+ Khi chia 7 cho 3 được thương là 2,333…, chữ số 3 được lặp lại mãi. Nên là số thập phân vô hạn tuần hoàn với chu kì là 3.
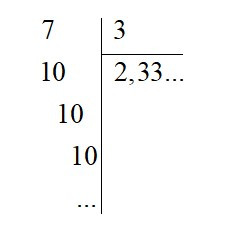
+ Phân số là số thập phân vô hạn tuần hoàn với chu kì là 72.
+ Phân số là số thập phân vô hạn tuần hoàn với chu kì là 1.
Chú ý:
• Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Ví dụ: Số ;
2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước
Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.
Ví dụ:
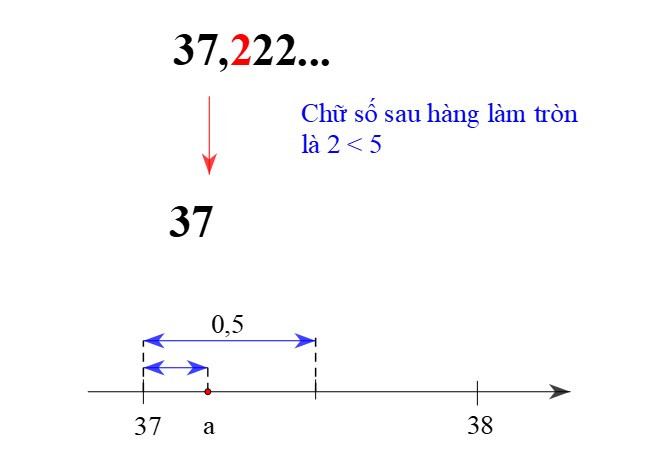
+ Làm tròn a = 37,222… đến hàng đơn vị thì được kết quả là 37. Ta viết 37,222… ≈ 37. Ta cũng nói rằng 37 là kết quả làm tròn của a = 37,222… với độ chính xác là 0,5.
+ Làm tròn số 17,213… đến hàng phần mười ta được kết quả 17,213… ≈ 17,2 với độ chính xác là 0,05.
+ Để làm tròn số 129,18 với độ chính xác là 5, ta làm tròn đến hàng chục. Ta được 129,18 ≈ 130.
Chú ý:
• Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng bảng dưới đây.
|
Hàng làm tròn |
Độ chính xác |
|
Trăm |
50 |
|
Chục |
5 |
|
Đơn vị |
0,5 |
|
Phần mười |
0,05 |
|
Phần trăm |
0,005 |
Đọc thêm
• Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân hữu hạn. Ví dụ:
• Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ:
• Mỗi số thập phân vô hạn tuần hoàn biểu diễn một số hữu tỉ. Ví dụ:
; ; ;
3. Số vô tỉ
• Số thập phân không phải số thập phân hữu hạn cũng không phải số thập phân vô hạn tuần hoàn được gọi là số thập phân vô hạn không tuần hoàn.
• Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Tập hợp các số vô tỉ kí hiệu là .
Ví dụ:
+ Tỉ số giữa chu vi và đường kính của một đường tròn luôn là số π (đọc là pi) và bằng 3,14159265358… đây là số vô tỉ.
Chú ý:
• Ta làm tròn số thập phân vô hạn như làm tròn số thập phân hữu hạn.
Ví dụ: Chẳng hạn ta làm tròn số 0,215679012… đến chữ số thập phân thứ ba.
Ta thấy chữ số thập phân thứ 4 là 6 > 5 nên làm tròn số 0,215679012… đến chữ số thập phân thứ ba ta được kết quả là 0,216.
4. Căn bậc hai số học
• Căn bậc hai số học của một số a không âm, kí hiệu là , là số x không âm sao cho x2 = a.
• Theo định nghĩa căn bậc hai số học ta có: với a ≥ 0.
Ví dụ:
+ Hình vuông có diện tích là 2 cm2 thì độ dài cạnh hình vuông gọi là căn bậc hai số học của 2 và bằng cm.
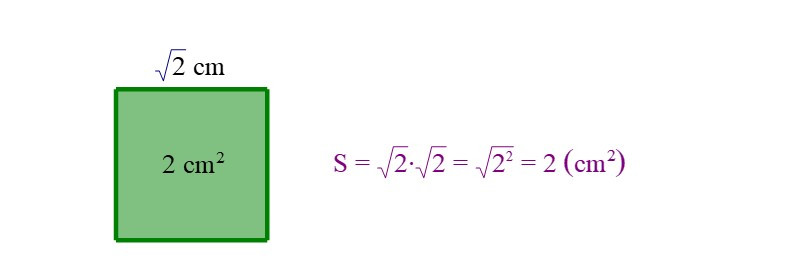
+ Tính: a) ; b)
Hướng dẫn giải
a) Vì 82 = 64 và 8 > 0 nên = 8;
b) Vì 159 > 0 nên = 159.
5. Tính căn bậc hai số học bằng máy tính cầm tay
• Căn bậc hai số học của một số tự nhiên không chính phương luôn là một số vô tỉ.
• Cách tính căn bậc hai số học của một số a không âm bằng máy tính cầm tay
Phép tính:
Ấn các phím theo thứ tự: (a là một số không âm bất kì trên bàn phím máy tính)

Ví dụ:
+ Muốn tính căn bậc hai số học của 2, ta có phép tính là và ấn máy tính như sau:

Ta được kết quả hiển thị trên màn hình là: 1,414213562
Đây là kết quả đã được làm tròn đến số thập phân số 9
Nên ta có: ≈ 1,414213562.
Chú ý:
• Màn hình máy tính cầm tay chỉ hiển thị được một số hữu hạn chữ số nên các kết quả là số thập phân vô hạn (tuần hoàn hay không tuần hoàn) đều được làm tròn.
6. Khái niệm số thực và trục số thực
• Số hữu tỉ và số vô tỉ được gọi chung là số thực.
Tập hợp số thực được kí hiệu là .
Ví dụ:
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số vô tỉ nên cũng là một số thực.
Chú ý:
• Cũng như số hữu tỉ, mỗi số thực a đều có một số đối kí hiệu là – a.
Ví dụ: Số đối của là ; số đối của là .
• Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
• Vì mỗi điểm trên trục số đều biểu diễn một số thực nên các số thực lấp đầy trục số. Người ta cũng gọi trục số là trục số thực.

• Trong tập hợp số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
Ví dụ: Tính giá trị của biểu thức ta làm như sau:
(Tính chất giao hoán)
(Tính chất kết hợp)
(Tổng hai số đối nhau luôn bằng 0)
(Cộng với số 0)
7. Thứ tự trong tập hợp các số thực
• Các số thực đều được viết dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể so sánh hai số thực bằng cách viết dưới dạng số thập phân.
• Cũng như các số hữu tỉ, ta có
Với hai số thực a và b bất kì ta luôn có a = b hoặc a < b hoặc a > b.
Cho ba số thực a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).
• Trên trục số thực, nếu a < b thì điểm a nằm trước điểm b. Các điểm nằm trước gốc O biểu diễn các số âm, các điểm nằm sau gốc O biểu diễn các số dương.
• x là số âm, ta viết: x < 0; x là số dương, ta viết: x > 0.
Ví dụ:
+ So sánh và – 1,5 ta làm như sau: nên .
+ So sánh và ta làm như sau: Vì và nên .
+ Ta có nên điểm biểu diễn của trên trục số nằm giữa hai điểm A và B.

Chú ý:
• Nếu 0 < a < b thì .
Ví dụ: 0 < 3 < 5 thì .
8. Giá trị tuyệt đối của một số thực
• Với số thực a tùy ý, ta có khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là .
• Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.
• Giá trị tuyệt đối của 0 là 0.
• Giá trị tuyệt đối của một số dương là chính nó.
• Giá trị tuyệt đối của một số âm là số đối của nó.
Ví dụ:
+ Số 1 và –1 là hai số đối nhau và có cùng giá trị tuyệt đối là 1

+ Số nên
+ Số nên