Với giải sách bài tập Toán 7 Bài 7: Tập hợp các số thực sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 7: Tập hợp các số thực

Giải SBT Toán 7 trang 31 Tập 1

Bài 2.22 trang 31 sách bài tập Toán lớp 7 Tập 1:Kí hiệu $\mathbb{N};\mathbb{Z};\mathbb{Q};\mathrm{𝕀};ℝ$ theo thứ tự là tập hợp các số tự nhiên, tập hợp các số nguyên, tập hợp các số hữu tỉ, tập hợp các số vô tỉ và tập hợp các số thực. Khẳng định nào sau đấy sai?

A. Nếu $x\in \mathbb{N}$ thì $x\in \mathbb{Z}$;

B. Nếu $x\in ℝ$ và $x\notin \mathbb{Q}$ thì $x\in 𝕀$;

C. $1\in ℝ$;

D. Nếu $x\notin 𝕀$ thì x viết được thành số thập phân hữu hạn.

Lời giải:

A. Nếu x ∈ ℕ thì x ∈ ℤ

Khẳng định A đúng vì tất cả các số tự nhiên đều là số nguyên;

B. Nếu x ∈ ℝ và x ∉ ℚ thì $x\in 𝕀$

Khẳng định B đúng vì tập số thực gồm có số hữu tỉ và số vô tỉ nên nếu x không là số hữu tỉ thì x là số vô tỉ.

C. 1 ∈ ℝ

Khẳng định C đúng vì 1 là số thực.

D. Nếu $x\notin 𝕀$ thì x viết được thành số thập phân hữu hạn

Khẳng định D sai vì nếu x không là số vô tỉ thì x là số hữu tỉ mà số hữu tỉ gồm số thập phân hữu hạn và số thập phân vô hạn tuần hoàn nên khẳng định D sai.

Vậy khẳng định sai là D.

Bài 2.23 trang 31 sách bài tập Toán lớp 7 Tập 1: Xét tính đúng, sai của các khẳng định sau:

a) Nếu x là số hữu tỉ thì x là số thực;

b) 2 không phải là số hữu tỉ;

c) Nếu x là số nguyên thì $\sqrt{x}$ là số thực;

d) Nếu x là số tự nhiên thì $\sqrt{x}$ là số vô tỉ.

Lời giải:

a) Nếu x là số hữu tỉ thì x là số thực. Khẳng định này đúng vì mọi số hữu tỉ đều là số thực.

b) 2 không phải là số hữu tỉ. Khẳng định này sai vì 2 là số nguyên nên 2 là số hữu tỉ.

c) Nếu x là số nguyên thì $\sqrt{x}$ là số thực. Khẳng định này sai vì nếu x < 0 thì không tồn tại $\sqrt{x}$.

d) Nếu x là số tự nhiên thì $\sqrt{x}$ là số vô tỉ. Khẳng định này sai vì nếu x = 25 thì $\sqrt{x}=\sqrt{25}$ = 5 là số hữu tỉ.

Bài 2.24 trang 31 sách bài tập Toán lớp 7 Tập 1:Tìm số đối của các số thực sau: -2,1; -0,(1); $\frac{2}{\pi }$; 3 – $\sqrt{2}$.

Lời giải:

Số đối của số -2,1 là 2,1 vì (-2,1) + 2,1 = 0;

Số đối của số -0,(1) là 0,(1) vì -0,(1) + 0,(1) = 0;

Số đối của $\frac{2}{\pi }$ là $-\frac{2}{\pi }$ vì $\frac{2}{\pi }+\left(-\frac{2}{\pi }\right)$ = 0

Số đối của 3 – $\sqrt{2}$ là -3 + $\sqrt{2}$ vì 3 – $\sqrt{2}$ + (-3) + $\sqrt{2}$ = 0.

Giải SBT Toán 7 trang 32 Tập 1

Bài 2.25 trang 32 sách bài tập Toán lớp 7 Tập 1: So sánh a = 1,(41) và $\sqrt{2}$.

Lời giải:

a = 1,(41) = 1,414141….

$\sqrt{2}$= 1,414213...

Kể từ trái sang phải, chữ số cùng hàng đầu tiên khác nhau nằm ở hàng phần chục nghìn. Mà 1 < 2 nên 1,414141… < 1,414213…

Do đó, a = 1,(41) < $\sqrt{2}$.

Bài 2.26 trang 32 sách bài tập Toán lớp 7 Tập 1:Viết các số thực sau theo thứ tự từ bé đến lớn:

$\sqrt{5};-1,7\left(5\right);\pi ;-2;\frac{22}{7};0$.

Lời giải:

Ta chia các số thực đã cho thành ba nhóm.

Nhóm số thực không âm, không dương: 0

Nhóm số thực âm: -1,7(5); -2;

Nhóm số thực dương: $\sqrt{5};\pi ;\frac{22}{7}$

Ta đi so sánh nhóm số thực âm.

Thay vì so sánh -1,7(5) và -2 ta đi so sánh hai số đối của chúng là 1,7(5) và 2.

Nhận thấy 1,7(5) có phần nguyên là 1 < 2 nên 1,7(5) < 2. Do đó, -1,7(5) > -2.

Ta đi so sánh nhóm số thực dương.

$\sqrt{5}=2,\mathrm{23606...}$

$\pi =3,\mathrm{1215926...}$

$\frac{22}{7}=3,\mathrm{14287...}$

Ta thấy 2 < 3 nên số nào có phần nguyên là 2 sẽ bé hơn số có phần nguyên là 3. Do đó, $\sqrt{5}$ nhỏ nhất trong ba số.

Ta đi so sánh π và $\frac{22}{7}$.

Ta có: π = 3,1415926...

$\frac{22}{7}$ = 3,14287...

Nhận thấy chữ số cùng hàng đầu tiên khác nhau là chữ số hàng nghìn. Vì 1 < 2 nên 3,1415926… < 3,14287…hay $\pi <\frac{22}{7}$

Sắp xếp các số đã cho theo thứ tự từ bé đến lớn như sau:

-2 < -1,7(5) < 0 < $\sqrt{5}<\pi <\frac{22}{7}$.

Bài 2.27 trang 32 sách bài tập Toán lớp 7 Tập 1:Tìm các số thực x có giá trị tuyệt đối bằng 1,6(7). Điểm biểu diễn các số thực tìm được nằm trong hay nằm ngoài khoảng giữa hai điểm -2 và 2,(1) trên trục số?

Lời giải:

Ta có:

|x| = 1,6(7) nên x = 1,6(7) hoặc x = -1,6(7)

Ta so sánh 1,6(7) với -2 và 2,(1)

Vì 1,6(7) là số thực dương còn -2 là số thực âm nên 1,6(7) > -2.

Lại có phần nguyên của 1,6(7) là 1 và phần nguyên của 2,(1) là 2 nên 1,6(7) < 2.

Vậy 1,6(7) nàm trong khoảng -2 và 2,(1).

Ta so sánh -1,6(7) với -2 và 2,(1)

Ta có: -1,6(7) là số thực âm và 2,(1) là số thực dương nên -1,6(7) < 2,(1).

Số đối của -1,6(7) là 1,6(7) và số đối của -2 là 2. Vì 1,6(7) có phần nguyên là 1 < 2 nên 1,6(7) < 2. Do đó, -1,6(7) > -2.

Vậy -1,6(7) nằm trong khoảng -2 và 2,(1).

Bài 2.28 trang 32 sách bài tập Toán lớp 7 Tập 1: Xác định dấu và giá trị tuyệt đối của các số thực sau:

a) -1,3(51);

b) $1-\sqrt{2}$;

c) $\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)$

Lời giải:

a) -1,3(51) mang dấu âm và |-1,3(51)| = 1,3(51).

b) $1-\sqrt{2}$

Vì 1 < 2 nên $\sqrt{1}<\sqrt{2}$ hay 1 < $\sqrt{2}$

Do đó 1 – $\sqrt{2}$ < 0 nên 1 – $\sqrt{2}$ mang dấu âm.

|1 – $\sqrt{2}$| = -(1 – $\sqrt{2}$) = $\sqrt{2}$ - 1.

c) $\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)$

Vì 9 > 2 nên $\sqrt{9}>\sqrt{2}$ hay 3 > $\sqrt{2}$. Do đó, $3-\sqrt{2}$ > 0.

Lại có 4 < 5 nên $\sqrt{4}<\sqrt{5}$ hay $2<\sqrt{5}$. Do đó, 2 – $\sqrt{5}$ < 0.

Vì $3-\sqrt{2}$ > 0 và 2 – $\sqrt{5}$ < 0 nên $\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)$ < 0

Ta có:

$\left(3-\sqrt{2}\right)\left(2-\sqrt{5}\right)=3.\left(2-\sqrt{5}\right)-\sqrt{2}.\left(2-\sqrt{5}\right)$

$=6-3\sqrt{5}-2\sqrt{2}+\sqrt{2}.\sqrt{5}$

$=6-3\sqrt{5}-2\sqrt{2}+\sqrt{10}$

Ta có:

$\left(6-3\sqrt{5}-2\sqrt{2}+\sqrt{10}\right)$

$=-\left(6-3\sqrt{5}-2\sqrt{2}+\sqrt{10}\right)$

$=-6+3\sqrt{5}+2\sqrt{2}-\sqrt{10}$

Bài 2.29 trang 32 sách bài tập Toán lớp 7 Tập 1:Không sử dụng máy tính cầm tay, ước lượng giá trị thập phân của số $\sqrt{3}$ với độ chính xác 0,05.

Lời giải:

Muốn ước lượng giá trị thập phân của $\sqrt{3}$ với độ chính xác 0,05 ta phải làm tròn số đó đến hàng phần mười.

Trong ví dụ 3 (trang 32) ta thấy 1,7 < $\sqrt{3}$ < 1,8. Cần xét xem $\sqrt{3}$ gần với 1,7 hơn hay 1,8 hơn. Muốn vậy ta xét số $\frac{1,7+1,8}{2}=1,75$ điểm biểu diễn số 1,75 cách đều 1,7 và 1,8.

Ta có (1,75)² = 3,0625, do đó 3 < (1,75)² < 1,75. Vì vậy $\sqrt{3}$ < $\sqrt{{\left(1,75\right)}^2}$

Suy ra, $\sqrt{3}<1,75$. Từ đó, 1,7 < $\sqrt{3}$ < 1,75. Vì vậy $\sqrt{3}$ gần 1,7 hơn so với 1,8.

Vậy làm tròn giá trị thập phân của $\sqrt{3}$ đến hàng phần mười (độ chính xác 0,05) ta được $\sqrt{3}\approx 1,7$.

Bài 2.30 trang 32 sách bài tập Toán lớp 7 Tập 1:Tính $\left(6-\sqrt{35}\right)+5+\sqrt{35}$

Lời giải:

Ta có 6 = $\sqrt{36}$ > $\sqrt{35}$ suy ra 6 – $\sqrt{35}$ > 0, do đó

$\left(6-\sqrt{35}\right)+5+\sqrt{35}$ = $6-\sqrt{35}$ + $5+\sqrt{35}$ = (6 + 5) + ($\sqrt{35}$ - $\sqrt{35}$)

= 11 + 0 = 11

Bài 2.31 trang 32 sách bài tập Toán lớp 7 Tập 1:Biết $\sqrt{11}$ là số vô tỉ. Trong các phép tính sau, những phép tính nào có kết quả là số hữu tỉ?

a) $\frac{1}{\sqrt{11}}$;

b) $\sqrt{11}.\sqrt{11}$;

c) 1 + $\sqrt{11}$;

d) ${\left(\sqrt{11}\right)}^4$.

Lời giải:

a) $\frac{1}{\sqrt{11}}$ phép tính này không cho ta kết quả là số hữu tỉ;

b) $\sqrt{11}.\sqrt{11}=\sqrt{11.11}=\sqrt{{11}^2}=11$ phép tính này cho ta kết quả là số hữu tỉ;

c) 1 + $\sqrt{11}$ phép tính này không cho ta kết quả là số hữu tỉ;

d) 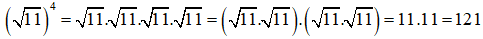phép tính này cho ta kết quả là số hữu tỉ.

Bài 2.32 trang 32 sách bài tập Toán lớp 7 Tập 1: Tính giá trị của các biểu thức sau:

a) $\sqrt{0,25}-\sqrt{0,49}$;

b) 0,2.$\sqrt{100}-\sqrt{0,25}$.

Lời giải:

a) $\sqrt{0,25}-\sqrt{0,49}=\sqrt{0,5^2}-\sqrt{0,7^2}$ = 0,5 – 0,7 = 0,2;

b) 0,2.$\sqrt{100}-\sqrt{0,25}$$=0,2.\sqrt{{10}^2}-\sqrt{0,5^2}$ = 0,2.10 – 0,5 = 2 – 0,5 = 1,5.

Bài 2.33 trang 32 sách bài tập Toán lớp 7 Tập 1:So sánh a = 0,(12) và b = 0,1(21).

Lời giải:

Ta thấy 100a = 12(12) = 12 + a nên 99a = 12, suy ra a = $\frac{12}{99}$.

Tương tự, b = 0,1 + 0,0(21) = $\frac{1}{10}+\frac{1}{10}.0,\left(21\right)$

Đặt x = 0,(21) thì 100x = 21,(21) = 21 + x suy ra x = $\frac{21}{99}$

Và b = $\frac{1}{10}+\frac{1}{10}.\frac{21}{99}=\frac{1}{10}\left(1+\frac{21}{99}\right)$$=\frac{1}{10}.\frac{120}{99}=\frac{12}{99}$.

Vậy a = b

Bài 2.34 trang 32 sách bài tập Toán lớp 7 Tập 1:Tìm giá trị nhỏ nhất của biểu thức A = $2+3\sqrt{x^2+1}$.

Lời giải:

Ta có: x² ≥ 0 với mọi số thực x nên x² + 1 ≥ 1 với mọi số thực x.

Suy ra: $\sqrt{x^2+1}\ge \sqrt{1}$ nên $\sqrt{x^2+1}\ge 1$.

Vì $\sqrt{x^2+1}\ge 1$ nên $3.\sqrt{x^2+1}\ge 3.1$ hay $3.\sqrt{x^2+1}\ge 3$

Suy ra A = 2 + $3.\sqrt{x^2+1}\ge$2+3=5

Vậy A_min = 5 khi x = 0.

Bài 2.35 trang 32 sách bài tập Toán lớp 7 Tập 1:Tìm giá trị nhỏ nhất của biểu thức B = |x – 1| + |x – 3|.

Lời giải:

Xét các điểm biểu diễn số thực x trên trục số. Biểu thức đã cho đúng bằng tổng các khoảng cách từ x tới hai điểm 1 và 3. Nếu x nằm ngoài đoạn giữa 1 và 3 thì tổng hai khoảng cách trên lớn hơn khoảng cách giữa 1 và 3. Nếu x nằm trong đoạn giữa 1 và 3 thì tổng hai khoảng cách nói trên đúng bằng khoảng cách giữa 1 và 3. Vì vậy, biểu thức B đã cho có giá trị nhỏ nhất là 2 (đạt được khi 1 ≤ x ≤ 2).

Bài 2.36 trang 32 sách bài tập Toán lớp 7 Tập 1:Hãy giải thích tại sao |x + y| ≤ |x| + |y| với mọi số thực x, y.

Lời giải:

Xét hai trường hợp:

Nếu x + y ≥ 0 thì |x + y| = x + y ≤ |x| + |y| (vì x ≤ |x| với mọi số thực x)

Nếu x + y < 0 thì |x + y| = –x – y ≤ |-x| + |-y| = |x| + |y|.

Vậy với mọi x, y là số thực thì ta luôn có |x + y| ≤ |x| + |y|.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 6: Số vô tỉ. Căn bậc hai số học

Bài 7: Tập hợp các số thực

Ôn tập chương 2

Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

Lý thuyết Tập hợp các số thực

1. Khái niệm số thực và trục số thực

• Số hữu tỉ và số vô tỉ được gọi chung là số thực.

Tập hợp số thực được kí hiệu là $\mathrm{ℝ}$.

Ví dụ:

+ Số $0,6=\frac{3}{5}$ là một số hữu tỉ nên cũng là một số thực.

+ Số $-2=\frac{-2}{1}$ là một số hữu tỉ nên cũng là một số thực.

+ Số $\sqrt{2}=1,\mathrm{4142...}$ là một số vô tỉ nên cũng là một số thực.

Chú ý:

• Cũng như số hữu tỉ, mỗi số thực a đều có một số đối kí hiệu là – a.

Ví dụ: Số đối của $\sqrt{2}$ là $-\sqrt{2}$;  số đối của $-\frac{3}{5}$ là $\frac{3}{5}$.

• Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

• Vì mỗi điểm trên trục số đều biểu diễn một số thực nên các số thực lấp đầy trục số. Người ta cũng gọi trục số là trục số thực.

• Trong tập hợp số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.

Ví dụ: Tính giá trị của biểu thức $-\sqrt{2}+\frac{9}{4}+\sqrt{2}-\frac{5}{4}$ ta làm như sau:

$-\sqrt{2}+\frac{9}{4}+\sqrt{2}-\frac{5}{4}$

$=-\sqrt{2}+\sqrt{2}+\frac{9}{4}-\frac{5}{4}$                    (Tính chất giao hoán)

$=\left(-\sqrt{2}+\sqrt{2}\right)+\left(\frac{9}{4}-\frac{5}{4}\right)$             (Tính chất kết hợp)

$=0+\frac{4}{4}$                                         (Tổng hai số đối nhau luôn bằng 0)

$=0+1=1$                                     (Cộng với số 0)

2. Thứ tự trong tập hợp các số thực

• Các số thực đều được viết dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể so sánh hai số thực bằng cách viết dưới dạng số thập phân.

• Cũng như các số hữu tỉ, ta có

  Với hai số thực a và b bất kì ta luôn có a = b hoặc a < b hoặc a > b.

  Cho ba số thực a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số thực, nếu a < b thì điểm a nằm trước điểm b. Các điểm nằm trước gốc O biểu diễn các số âm, các điểm nằm sau gốc O biểu diễn các số dương.

 • x là số âm, ta viết: x < 0; x là số dương, ta viết: x > 0.

Ví dụ:

+ So sánh $-\sqrt{2}$ và ­– 1,5 ta làm như sau: $\sqrt{2}=1,\mathrm{4142...}<1,5$ nên $-\sqrt{2}>-1,5$.

+ So sánh $\sqrt{3}$ và $-\sqrt{5}$ ta làm như sau: Vì $\sqrt{3}>0$ và $-\sqrt{5}<0$ nên $\sqrt{3}>-\sqrt{5}$.

+ Ta có $1<\sqrt{3}<2$ nên điểm biểu diễn của $\sqrt{3}$ trên trục số nằm giữa hai điểm A và B.

Chú ý:

• Nếu 0 < a < b thì $\sqrt{\mathrm{a}}<\sqrt{\mathrm{b}}$.

Ví dụ: 0 < 3 < 5 thì $\sqrt{3}<\sqrt{5}$.

3. Giá trị tuyệt đối của một số thực

• Với số thực a tùy ý, ta có khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là $\left|\mathrm{a}\right|$.

• Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.

• Giá trị tuyệt đối của 0 là 0.

• Giá trị tuyệt đối của một số dương là chính nó.

• Giá trị tuyệt đối của một số âm là số đối của nó.

$\left|\mathrm{a}\right|=\left\{\begin{array}{l}\mathrm{a}\mathrm{khi}\mathrm{a}>0\\ -\mathrm{a}\mathrm{khi}\mathrm{a}<0\\ 0\mathrm{khi}\mathrm{a}=0\end{array}\right.$

Ví dụ:

+ Số 1 và –1 là hai số đối nhau và có cùng giá trị tuyệt đối là 1

$\left|1\right|=\left|-1\right|=1$

+ Số $\frac{3}{4}>0$ nên $\left|\frac{3}{4}\right|=\frac{3}{4}$

+ Số $-\sqrt{3}<0$ nên $\left|-\sqrt{3}\right|=-\left(-\sqrt{3}\right)=\sqrt{3}$