Với giải sách bài tập Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Giải SBT Toán 7 trang 39 Tập 1
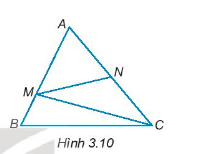
Bài 3.9 trang 39 Toán 7 Tập 1: Cho Hình 3.10.
a) Viết tên góc so le trong với góc NMC.
b) Viết tên góc đồng vị với góc ACB, góc AMN.
Lời giải:
a) Góc so le trong với góc NMC là góc MCB.
b) Góc đồng vị với góc ACB là góc ANM;
Góc đồng vị với góc AMN là góc ABC.
Lời giải:
Lời giải:
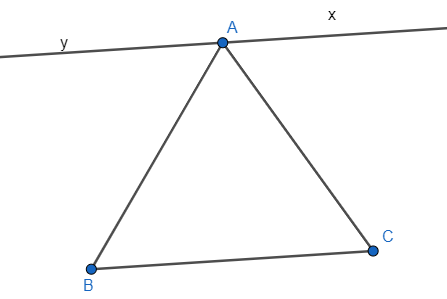
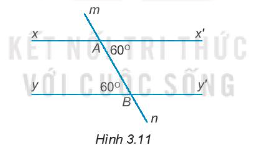
Bài 3.12 trang 39 Toán 7 Tập 1: Vẽ lại Hình 3.11 vào vở rồi giải thích tại sao xx’ // yy’.
Lời giải:
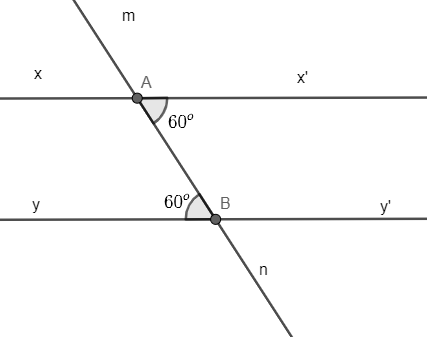
Ta có: Góc x’An và góc mBy là hai góc so le trong
Mặt khác
Do đó, hai đường thẳng xx’ và yy’ song song với nhau.
Bài 3.13 trang 39 Toán 7 Tập 1: Cho Hình 3.12. Giải thích tại sao a // b.
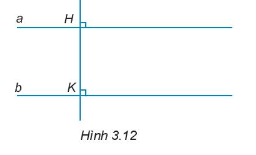
Lời giải:
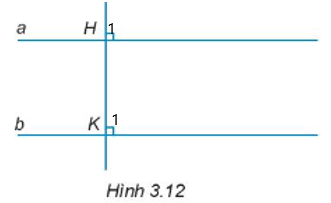
Vì HK vuông góc với a nên ;
Vì HK vuông góc với b nên .
Mà là hai góc đồng vị.
Do đó, a // b.
Giải SBT Toán 7 trang 40 Tập 1
Bài 3.14 trang 40 Toán 7 Tập 1: Cho Hình 3.13. Giải thích tại sao MN // PQ.
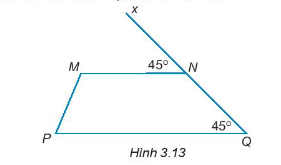
Lời giải:
Đường thẳng QN cắt đường thẳng MN và PQ lần lượt tại N và Q.
Từ hình vẽ ta thấy: ;
Mà hai góc này ở vị trí đồng vị.
Do đó MN // PQ.
Bài 3.15 trang 40 Toán 7 Tập 1: Cho Hình 3.14. Giải thích tại sao EF // NP.
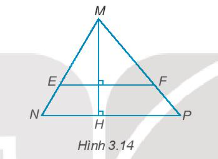
Lời giải:
Từ hình vẽ ta thấy:
MH vuông góc với NP; MH vuông góc với EF nên EF // NP (quan hệ từ vuông góc đến song song).
Bài 3.16 trang 40 Toán 7 Tập 1: Vẽ lại hình 3.15 vào vở, biết NP // MQ và NP = MQ.
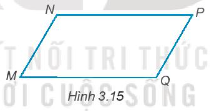
Lời giải:
Bài 3.17 trang 40 Toán 7 Tập 1: Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx //Ky.
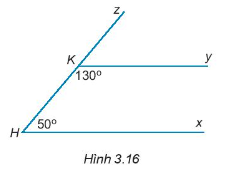
Lời giải:
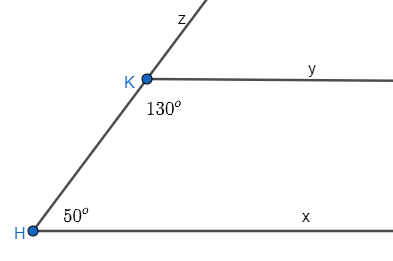
Vì góc và góc là hai góc kề bù.
Do đó, + = 180o
Thay số: + 130o = 180o
= 180o – 130o
= 50o.
Vì và là hai góc đồng vị và = = 50o.
Do đó, Ky // Hx.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
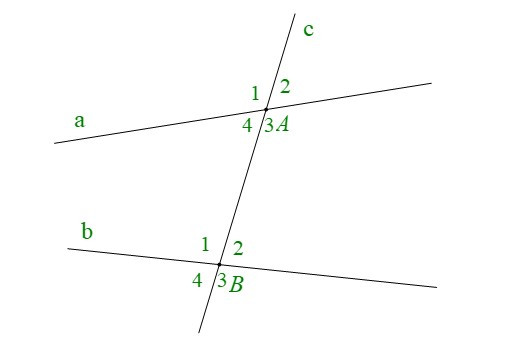
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Ví dụ:
+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.
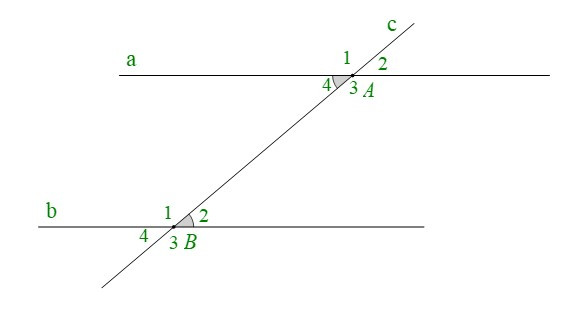
Ta có là cặp góc so le trong
Nếu thì cặp góc so le trong còn lại và các cặp góc đồng vị bằng nhau:
2. Dấu hiệu nhận biết hai đường thẳng song song
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: .
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
+ Cho hình vẽ:
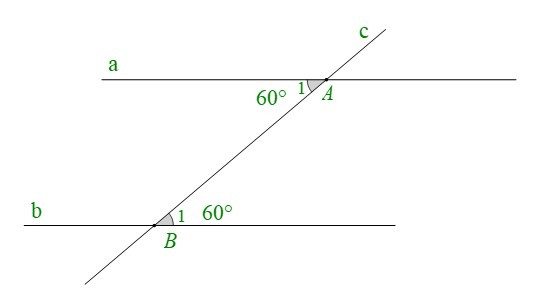
Ta có: . Mà hai góc ở vị trí so le trong.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
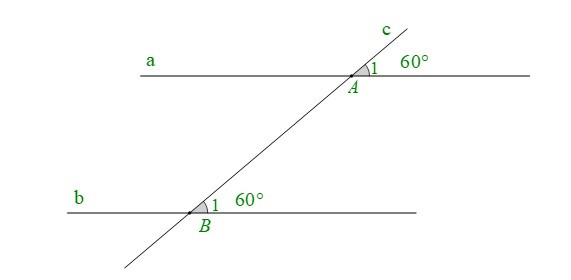
Ta có: . Mà hai góc ở vị trí đồng vị.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
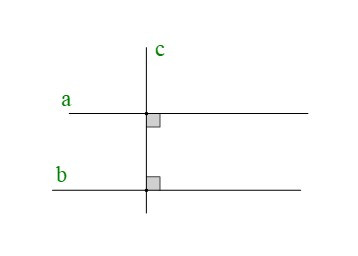
Ta có: và
Do đó: .
Chú ý:
+ Muốn vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước bằng góc 60° của êke ta làm như sau:
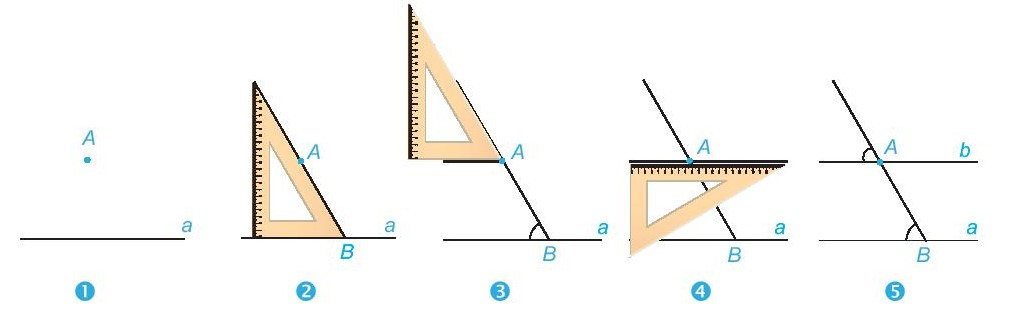
+ Tương tự ta có thể dùng góc vuông hoặc góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua một điểm và song song với đường thẳng cho trước.