Với giải vở thực hành Toán 7 Bài ôn tập cuối chương 2 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VTH Toán 7. Mời các bạn đón xem:

Giải VTH Toán lớp 7 Bài ôn tập cuối chương 2

Bài 1 (2.27) trang 34 VTH Toán 7 Tập 1: Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất:

$a=\sqrt{2},b=\sqrt{5}.$ Tính tổng hai số thập phân thu được.

Lời giải:

Sử dụng máy tính cầm tay ta tính được:

$\sqrt{2}=1,\mathrm{414213562...}\approx 1,4$ (làm tròn đến chữ số thập phân thứ nhất) và $\sqrt{5}=2,\mathrm{236067977...}\approx 2,2$.

Tổng hai số nhận được là: 1,4 + 2,2 = 3,6.

Bài 2 (2.28) trang 34 VTH Toán 7 Tập 1: Dùng thước dây có vạch chia để đo độ dài đường gấp khúc ABC trong Hình 2.1 (đơn vị xentimét, làm tròn đến chữ số thập phân thứ nhất). So sánh kết quả với kết quả của Bài tập 2.27.

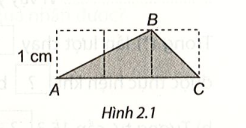
Lời giải:

Dùng thước dây có vạch chia để đo độ dài đường gấp khúc ABC với đơn vị xentimét ta thấy kết quả xấp xỉ bằng 3,6 cm (cũng là kết quả của Bài tập 2.27).

Bài 3 (2.29) trang 34 VTH Toán 7 Tập 1: Chia một sợi dây dài 10 m thành 7 đoạn bằng nhau.

a) Tính độ dài mỗi đoạn dây nhận được, viết kết quả dưới dạng số thập phân vô hạn tuần hoàn.

b) Dùng 4 đoạn dây nhận được ghép thành một hình vuông. Gọi C là chu vi của hình vuông đó. Hãy tìm C bằng hai cách sau rồi so sánh hai kết quả:

Cách 1. Dùng thước dây có vạch chia để đo, lấy chính xác đến xentimét.

Cách 2. Tính $C=4.\frac{10}{7},$ viết kết quả dưới dạng số thập phân với độ chính xác 0,005.

Lời giải:

a) Độ dài mỗi đoạn dây là 10 m: 7 = $\frac{10}{7}$ (m).

Viết kết quả dưới dạng số thập phân ta được: $\frac{10}{7}=1,\mathrm{428571428...}=1,\left(428571\right)$ m.

b) Cách 1: Dùng thước dây ta đo được C xấp xỉ bằng 5,72 (m) = 0,0572 (cm).

Cách 2. $C=4.\frac{10}{7}=\frac{40}{7}=5,\left(714285\right)$$=5,\mathrm{714285714285...}$Viết kết quả với độ chính xác 0,005 ta phải làm tròn kết quả đến hàng phần trăm: C ≈ 5,71 (m) = 0,0571 (cm).

Bài 4 (2.30) trang 35 VTH Toán 7 Tập 1: a) Cho hai số thực a = –1,25 và b = –2,3. So sánh: a và b; $\left|\mathrm{a}\right|$ và $\left|\mathrm{b}\right|$

b) Ta có nhận xét: Trong hai số âm, số nào có giá trị tuyệt đối lớn hơn là số bé hơn.

Em hãy áp dụng nhận xét này để so sánh –12,7 và –7,12.

Lời giải:

a) Nếu a =  – 1,25 và b = – 2,3 thì b < a vì a, b là hai số âm và 2,3 > 1,25. Mặt khác, |b| = 2,3 > 1,25 = |a|. Như vậy ta thấy a và b là hai số âm, b có giá trị tuyệt đối lớn hơn giá trị tuyệt đối của a, b là số nhỏ hơn a.

b) Ta có |– 12,7| = 12,7 > 7,12 = |– 7,12|. Suy ra –12,7 < –7,12.

Bài 5 (2.31) trang 35 VTH Toán 7 Tập 1: Cho hai số thực a = 2,1 và b = –5,2.

a) Em có nhận xét gì về hai tích a.b và – |a|.|b|?

b) Ta có cách nhân hai số khác dấu như sau: Muốn nhân hai số khác dấu, ta nhân các giá trị tuyệt đối của chúng rồi đặt dấu “–“ trước kết quả.

Em hãy áp dụng quy tắc trên để tính (–2,5).3.

Lời giải:

a) Nếu a = 2,1 và b = – 5,2 thì a.b = 2,1 . (– 5,2) =  – 10,92 và – |a|.|b| = – |2,1|.|– 5,2| =  – 2,1 . 5,2 = – 10,92. Như vậy a.b = – |a|.|b|.

b) Áp dụng quy tắc trên, có $\left(-2,5\right).3=-\left|-2,5\right|.\left|3\right|=-2,5.3=-7,5.$