Với giải Bài 3 trang 86 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 1: Khái niệm vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 1: Khái niệm vecto
Bài 3 trang 86 Toán lớp 10: Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16).
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng .
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng .
Phương pháp giải:
a) Bước 1: Tìm độ dài các cạnh
Bước 2: Xác định hướng của các vectơ có độ dài bằng
Bước 3: Từ bước 2, chỉ ra hai vectơ cùng hướng
Lời giải:
a)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng là:
và ; và ; và ; và
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là .
Do đó hai vectơ đối nhau và có độ dài bằng là:
và ; và .
Bài tập vận dụng:
Bài 1. a) Hãy tìm sự khác biệt giữa hai đại lượng sau:
(1) Bác Hai có số tiền là 50 triệu đồng.
(2) Một cơn bão di chuyển với vận tốc 18 km/h theo hướng tây tây bắc.
b) Trong các đại lượng giá tiền, thể tích, độ dịch chuyển, vận tốc, đại lượng nào cần được biểu diễn bởi vectơ?
Hướng dẫn giải
a) (1) Số tiền 50 triệu đồng là đại lượng vô hướng vì đại lượng này chỉ có độ lớn.
(2) Cơn bão di chuyển là đại lượng có hướng vì đại lượng này có cả độ lớn (18 km/h) và hướng (tây tây bắc).
b) Đại lượng cần được biểu diễn dưới dạng vectơ là đại lượng có hướng.
Ta thấy giá tiền, thể tích là đại lượng vô hướng vì chỉ có độ lớn.
Ta có độ dịch chuyển, vận tốc là đại lượng có hướng vì bao gồm cả độ lớn và hướng.
Do đó đại lượng cần được biểu diễn bởi vectơ là: độ dịch chuyển, vận tốc.
Bài 2. Cho hình chữ nhật ABCD. Gọi M là trung điểm đoạn BC.
a) Gọi tên các vectơ cùng hướng với .
b) Gọi tên các vectơ ngược hướng với .
c) Chỉ ra các cặp vectơ bằng nhau và đối nhau có các điểm đầu hoặc điểm cuối là A, B, C, D, M.
Hướng dẫn giải
 a) Vectơ-không cùng phương, cùng hướng với mọi vectơ nên cùng hướng với .
a) Vectơ-không cùng phương, cùng hướng với mọi vectơ nên cùng hướng với .
Các vectơ cùng hướng với vectơ và khác là các vectơ có giá song song hoặc trùng với và có hướng từ trên xuống dưới giống như .
Các vectơ thỏa mãn 2 điều kiện trên là: .
Vậy có 4 vectơ thỏa mãn yêu cầu bài toán là: .
b) Vì vectơ-không cùng phương, cùng hướng với mọi vectơ nên vectơ đối của vectơ-không ngược hướng với .
Vectơ đối của vectơ-không là chính nó nên ngược hướng với vectơ .
Các vectơ ngược hướng với là các vectơ có giá song song hoặc trùng với và có hướng ngược lại với , nghĩa là các vectơ cần tìm có hướng dưới lên trên.
Các vectơ thỏa mãn 2 điều kiện trên là: .
Vậy có 5 vectơ thỏa mãn yêu cầu bài toán là: .
c) - Vì ABCD là hình chữ nhật nên AB // CD và AB = CD (tính chất hình chữ nhật)
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
+ Tương tự ta có: và
+ M là trung điểm của BC nên BM = MC =
Mà hai vectơ cùng hướng và hai vectơ cúng hướng.
Do đó và
- và là hai vectơ cùng độ dài nhưng ngược hướng nên
Do đó và là hai vectơ đối nhau.
Tương tự ta có các cặp vectơ đối nhau là: và ; và và ; và và
Bài 3. Cho tứ giác ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi .
Hướng dẫn giải
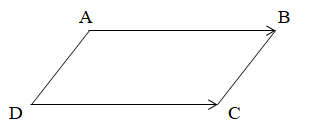 - Chứng minh chiều thuận: Tứ giác ABCD là hình bình hành thì
- Chứng minh chiều thuận: Tứ giác ABCD là hình bình hành thì
Vì ABCD là hình bình hành nên ta có AB // DC và AB = DC (tính chất hình bình hành)
Mà cùng hướng.
Do đó .
Vậy ABCD là hình bình hành (1).
- Chứng minh chiều đảo: thì tứ giác ABCD là hình bình hành.
Vì nên ta có cùng hướng và .
Do đó AB // DC và AB = DC.
Ta suy ra ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Vậy ABCD là hình bình hành (2).
Từ (1) (2), ta suy ra: ABCD là hình bình hành khi và chỉ khi .
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 3 trang 84 Toán lớp 10: Quan sát Hình 8 và gọi tên các vectơ:...
Thực hành 4 trang 84 Toán lớp 10: Khẳng định sau đây đúng hay sai? Hãy giải thích...
Thực hành 6 trang 86 Toán lớp 10: Tìm độ dài của các vectơ trong Ví dụ 5...
Bài 1 trang 86 Toán lớp 10: a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:...
Bài 6 trang 87 Toán lớp 10: Gọi O là tâm hình lục giác đều ABCDEF...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vecto
Bài 3: Tích của một số với một vecto
Bài 4: Tích vô hướng của hai vecto