Với giải sách bài tập Toán 10 Bài 1: Khái niệm vectơ sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 1: Khái niệm vectơ
Giải SBT Toán 10 trang 91 Tập 1
Bài 1 trang 91 SBT Toán 10 Tập 1: Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Chiếc xe máy có giá tiền là 30 triệu đồng.
- Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam.
Lời giải:
- Chiếc xe máy có giá tiền là 30 triệu đồng: đại lượng vô hướng.
- Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam: đại lượng chỉ rõ giá trị và hướng.
Nhiệt độ, lực, thể tích, tuổi, độ dịch chuyển, vận tốc.
Lời giải:
Các đại lượng cần được biểu diễn bởi vectơ: lực, độ dịch chuyển, vận tốc bởi đây là những đại lượng có hướng.
a) Gọi tên hai vectơ cùng hướng với .
b) Gọi tên hai vectơ ngược hướng với .
Lời giải:
a) Hai vectơ cùng hướng với : và .
b) Hai vectơ ngược hướng với : và .
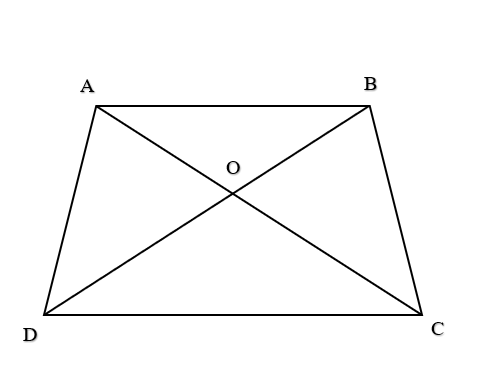
Bài 4 trang 91 SBT Toán 10 Tập 1: Cho hình thoi ABCD cạnh bằng a có tâm O và = 60°.
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng .
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng a.
Lời giải:
a) Ta có hình thoi ABCD có cạnh a. AO là tia phân giác của ( tính chất hình thoi ) ⇒ = 30°.
AC ⊥ BD ( tính chất hình thoi ) ⇒ = 90° ⇒ Tam giác AOD vuông tại O.
Xét tam giác AOD vuông tại O: cos = cos30° = ⇒ AO = a. cos30° = .
Hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường ( tính chất hình thoi )
⇒ AO = OC = .
Vậy ta có hai vectơ và bằng nhau và có độ dài bằng .
b) Ta có AC = AO + OC = a.
Vậy ta có hai vectơ và đối nhau và có độ dài a.
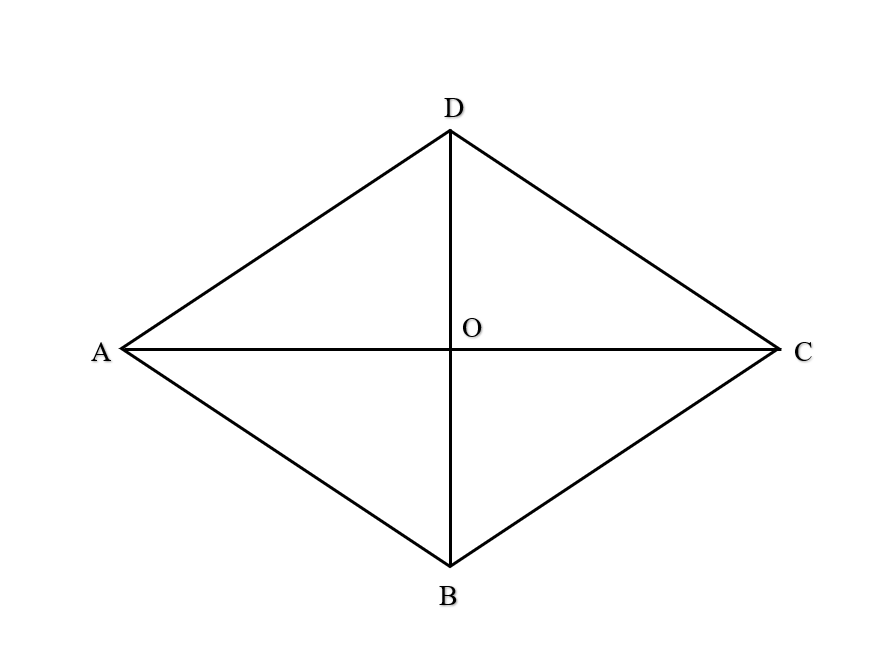
a) cùng hướng;
Lời giải:
a) cùng hướng với .
b) ngược hướng với .
c) ( do có cùng hướng và AB = DC ).
Bài 6 trang 91 SBT Toán 10 Tập 1: Gọi O là tâm của hình bát giác đều ABCDEFGH.
a) Tìm hai vectơ khác và cùng hướng với .
Lời giải:
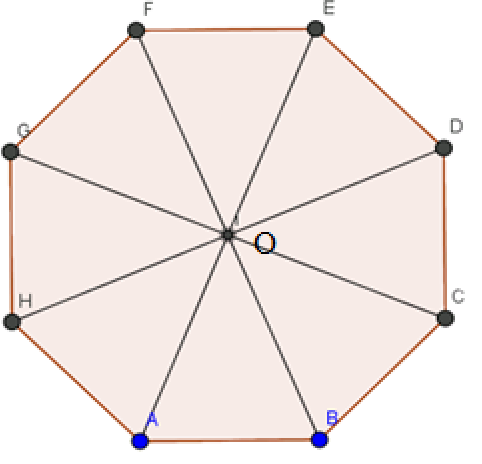
a) Hai vectơ khác và cùng hướng với : , .
b) Ta có: ⇒ DH vuông góc với FB.
Xét tứ giác FDBH: Hai đường chéo DH và FB vuông góc với nhau tại O là trung điểm của mỗi đường nên FDBH là hình thoi. ( DHNB hình thoi )
Lại có FB = DH ( do đều là đường chéo của bát giác đều ) nên FDBH là hình vuông. (DHNB hình vuông )
⇒ HF = BD và HF // BD.
Như vậy ta có vectơ bằng vectơ là .
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vectơ
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ
Lý thuyết Khái niệm vectơ
1. Định nghĩa vectơ
Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.
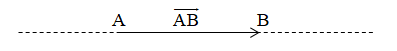
+ Vectơ có điểm đầu là A, điểm cuối là B được kí hiệu là
, đọc là vectơ .
+ Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ .
+ Độ dài của đoạn thẳng AB gọi là độ dài của và được kí hiệu là . Như vậy ta có .
Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là
Ví dụ: Cho tam giác ABC cân tại A có AB = AC = 2a, BC = . Gọi M là trung điểm BC. Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ: .
Hướng dẫn giải
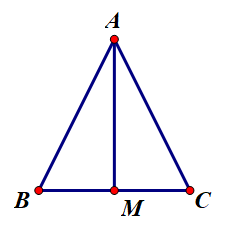
+ Vectơ :
có điểm đầu là B, điểm cuối là A và có giá là đường thẳng AB.
Ta có: = BA = 2a.
+ Vectơ :
có điểm đầu là M, điểm cuối là B và có giá là đường thẳng MB.
Vì M là trung điểm BC nên BM = .
Do đó .
+ Vectơ :
có điểm đầu là A, điểm cuối là M và có giá là đường thẳng AM.
Tam giác ABC cân tại A có AM là đường trung tuyến (do M là trung điểm BC).
Do đó AM cũng là đường cao của tam giác cân ABC.
Suy ra AM ⊥ BC.
Tam giác ABM vuông tại M: AM2 = AB2 – BM2 (Định lý Py ‒ ta ‒ go)
⇔ AM2 = 4a2 – 3a2 = a2.
Ta suy ra AM = a.
Do đó = AM = a.
2. Hai vectơ cùng phương, cùng hướng
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Ví dụ: Tìm các vectơ cùng phương trong hình bên dưới.
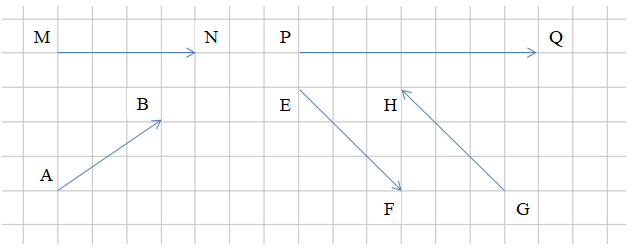
Hướng dẫn giải
Trong hình trên, ta có:
+) có giá là đường thẳng MN, có giá là đường thẳng PQ, mà hai đường thẳng MN và PQ trùng nhau.
Do đó và là hai vectơ cùng phương vì chúng có giá trùng nhau.
+) Ta có: có giá là đường thẳng EF, có giá là đường thẳng GH, mà hai đường thẳng EF và GH song song với nhau.
Do đó và là hai vectơ cùng phương vì chúng có giá song song.
Chú ý:
+ Trong hình trên, hai vectơ và cùng phương và có cùng hướng đi từ trái sang phải. Ta nói và là hai vectơ cùng hướng.
+ Hai vectơ và cùng phương nhưng ngược hướng với nhau ( có hướng từ trên xuống dưới và có hướng từ dưới lên trên). Ta nói hai vectơ và là hai vectơ ngược hướng.
Nhận xét:
+ Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.
+ Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ và cùng phương.
Giải thích: Ta thấy nếu ba điểm A, B, C thẳng hàng thì hai vectơ và có giá trùng nhau nên chúng cùng phương. Ngược lại, nếu hai vectơ và cùng phương thì ta suy ta hai đường thẳng AB và AC phải song song hoặc trùng nhau. Mà hai đường thẳng này có điểm A là điểm chung, do đó đường thẳng AB và AC trùng nhau. Khi đó ta có ba điểm A, B, C thẳng hàng. Vì vậy, ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ và cùng phương.

3. Vectơ bằng nhau – Vectơ đối nhau
Hai vectơ và được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu .
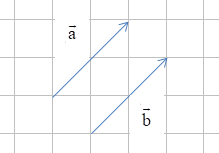
Hai vectơ và được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu . Khi đó vectơ được gọi là vectơ đối của vectơ .
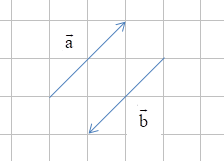
Chú ý:
+ Cho vectơ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho . Khi đó độ dài của là độ dài đoạn thẳng OA, kí hiệu là .
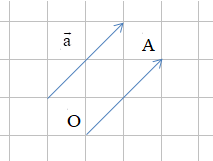
+ Cho đoạn thẳng MN, ta luôn có .
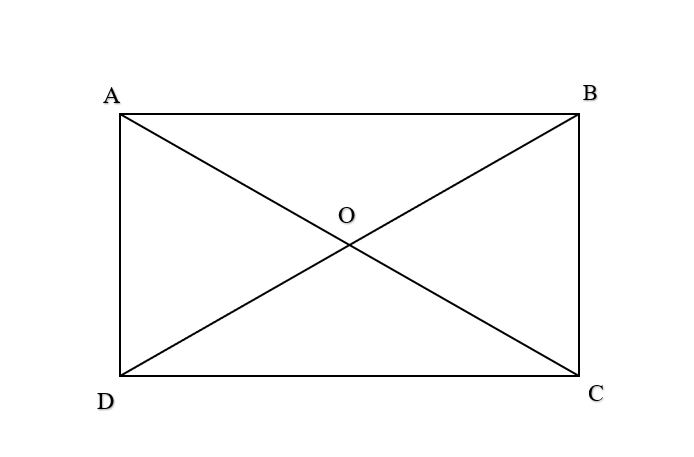
Ví dụ: Cho hình bình hành ABCD. Tìm các cặp vectơ bằng nhau và các cặp vectơ đối nhau.
Hướng dẫn giải
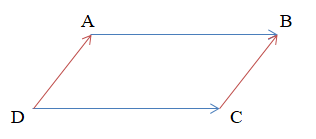
+ Các cặp vectơ bằng nhau:
Vì ABCD là hình bình hành nên ta có AB // DC và AB = DC (tính chất hình bình hành)
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
Tương tự, vì ABCD là hình bình hành nên ta có AD // BC và AD = BC.
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
Vậy ta có 4 cặp vectơ bằng nhau là: , , và .
+ Các cặp vectơ đối nhau:
Vì ABCD là hình bình hành nên ta có AB // DC và AB = DC (tính chất hình bình hành)
Mà hai vectơ ngược hướng và hai vectơ ngược hướng.
Do đó và .
Tương tự, vì ABCD là hình bình hành nên ta có AD // BC và AD = BC.
Mà hai vectơ ngược hướng và hai vectơ ngược hướng.
Do đó và .
Vậy ta có 4 cặp vectơ đối nhau là: , , và .
4. Vectơ-không
Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là .
Chú ý:
+ Quy ước: vectơ-không có độ dài bằng 0.
+ Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.
+ Mọi vectơ-không đều bằng nhau: , với mọi điểm A, B, C,...
+ Vectơ đối của vectơ-không là chính nó.
Ví dụ: Cho đoạn thẳng AB có độ dài bằng 4 cm. Gọi H là trung điểm của AB.
a) Tìm vectơ-không trong số các vectơ sau: .
b) Dùng kí hiệu để biểu diễn các vectơ-không đó.
c) Tính độ dài các vectơ ở câu a.
Hướng dẫn giải
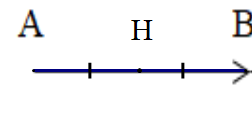 a) Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.
a) Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.
Do đó các vectơ-không là: .
b) Ta viết .
c) .
(cm).
Vì H là trung điểm AB nên AH = HB = (cm).
Do đó = AH = 2 (cm) và = HB = 2 (cm).