Phiếu bài tập tuần 23

Phiếu bài tập tuần 23 - Toán 7

Quý Lê Xuân Ngày: 08-03-2024 Lớp 7

Tải xuống 4 3 K 19

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập Phiếu bài tập tuần 23 - Toán 7, tài liệu bao gồm 4 trang, tuyển chọn các bài tập có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Phiếu bài tập tuần 23 - Toán 7 (ảnh 1)

PHIẾU HỌC TẬP TOÁN 7 TUẦN 23

Đại số 7 : Bài tập nhắc lại kiến thức Chương I + II

Hình học 7: Luyện tập các trường hợp bằng nhau của tam giác vuông

Bài 1: Tính giá trị các biểu thức sau (bằng cách hợp lý nếu có thể):

a) $\frac{7}{8} - 2 \frac{5}{6} + 1, 25$ b) $\frac{- 8}{3} : (\frac{- 4}{3}) : \frac{2}{5} . (- \frac{6}{5})$

c) $\frac{3}{5} - \frac{2}{5} : \frac{1}{5} + \frac{4}{5}$ d) $(\frac{3}{8} - \frac{5}{6} - \frac{2}{3}) : \frac{3}{4} . \frac{4}{3}$

e) $\frac{1}{4} .13 \frac{9}{11} + 0, 25.6 \frac{2}{11}$ f) $\frac{11}{13} : (- 2) + \frac{11}{13} : (- 3) + \frac{11}{13} : (- 6)$

Bài 2:

a) Cho $Δ A B C$ .Tính số đo các góc $\hat{A}$ , $\hat{B}$ , $\hat{C}$ biết số đo các góc $\hat{A}$ , $\hat{B}$ , $\hat{C}$ tỉ lệ nghịch với 3 ; 8; 6 .

b) Cho $Δ A B C$ có $5 \hat{C}$ $= \hat{A} + \hat{B}$ . Tính số đo các góc $\hat{A}$ , $\hat{B}$ , $\hat{C}$ biết $\hat{A} : \hat{B} = 2 : 3$

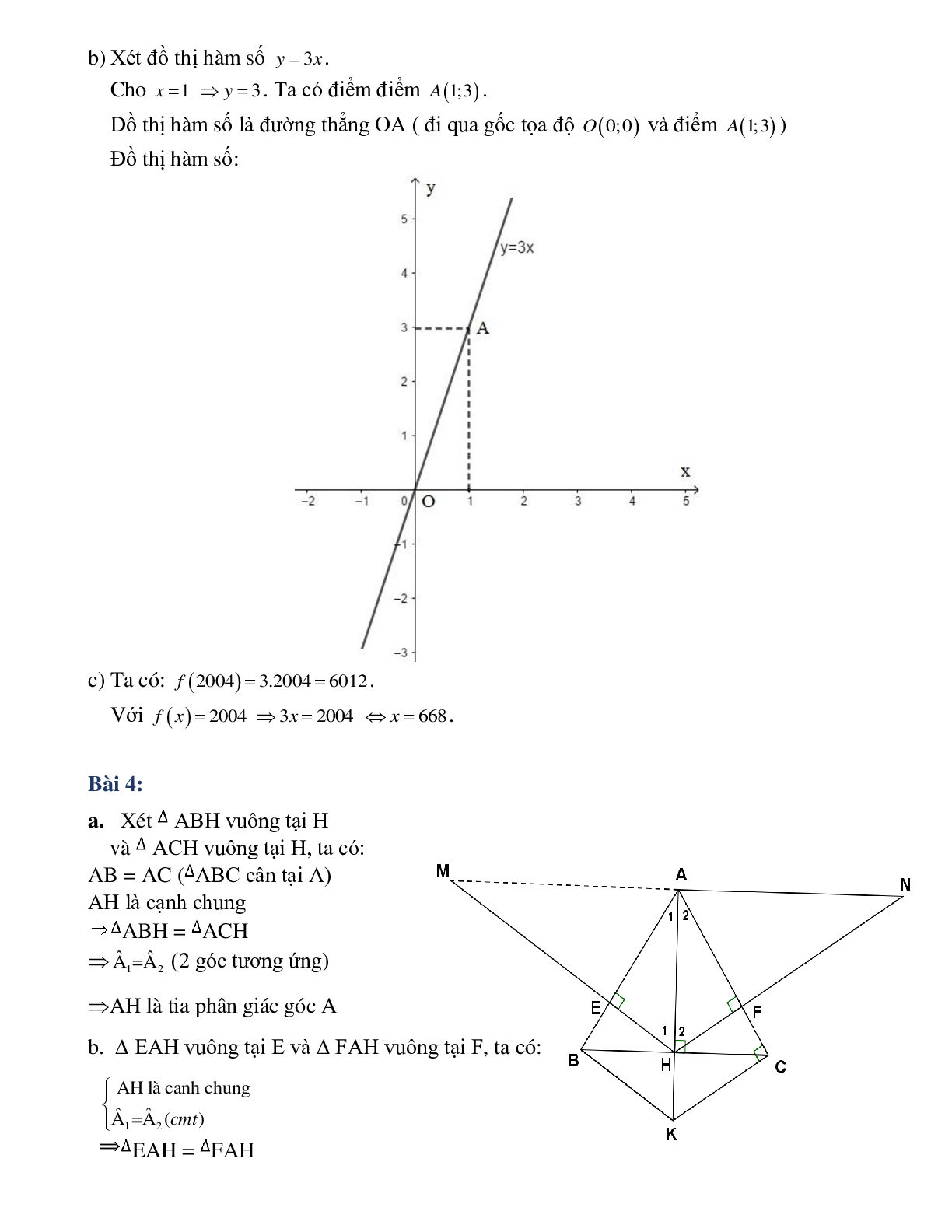
Bài 3: Cho hàm số $y = f (x) = (\frac{1}{3} - a) x$

a) Xác định hằng số $a$ nếu đồ thị hàm số đi qua điểm $A (1; 3)$ . Viết công thức của hàm số.

b) Vẽ đồ thị của hàm số cho bởi công thức trên.

c) Tính $f (2004)$ và tính $x$ biết $f (x) = 2004$ .

Bài 4: Cho ABC cân tại A (A<90⁰). Vẽ AH $⊥$ BC tại H

a) Chứng minh rằng: ABH = ACH rồi suy ra AH là tia phân giác góc A

b) Từ H vẽ HE $⊥$ AB tại E, HF $⊥$ AC tại F. Chứng minh rằng:

EAH = FAH rồi suy ra HEF là tam giác cân.

c) Đường thẳng vuông góc với AC tại C cắt tia AH tại K.
Chứng minh rằng: EH // BK.

d) Qua A, vẽ đường thẳng song song với BC cắt tia HF tại N. Trên tia HE lấy điểm M sao cho HM = HN. Chứng minh rằng: M, A, N thẳng hàng.

Hết

PHẦN HƯỚNG DẪN GIẢI

Bài 1:

Tính giá trị các biểu thức sau(bằng cách hợp lý nếu có thể):

a) $\frac{7}{8} - 2 \frac{5}{6} + 1, 25 = \frac{7}{8} - \frac{17}{6} + \frac{5}{4} = \frac{21 - 68 + 30}{24} = - \frac{17}{24}$

b) $\frac{- 8}{3} : (\frac{- 4}{3}) : \frac{2}{5} . (- \frac{6}{5}) = \frac{- 8}{3} . \frac{3}{- 4} . \frac{5}{2} . (- \frac{6}{5}) = - 6$

c) $\frac{3}{5} - \frac{2}{5} : \frac{1}{5} + \frac{4}{5} = \frac{3}{5} - \frac{2}{5} .5 + \frac{4}{5} = \frac{3 - 10 + 4}{5} = - \frac{3}{5}$

d) $(\frac{3}{8} - \frac{5}{6} - \frac{2}{3}) : \frac{3}{4} . \frac{4}{3} = \frac{9 - 20 - 16}{24} . \frac{4}{3} . \frac{4}{3} = \frac{- 27}{24} . \frac{4}{3} . \frac{4}{3} = - 2$

e) $\frac{1}{4} .13 \frac{9}{11} + 0, 25.6 \frac{2}{11} = \frac{1}{4} .13 \frac{9}{11} + \frac{1}{4} .6 \frac{2}{11} = \frac{1}{4} (13 \frac{9}{11} + 6 \frac{2}{11}) = \frac{1}{4} .20 = 5$

f) $\frac{11}{13} : (- 2) + \frac{11}{13} : (- 3) + \frac{11}{13} : (- 6) = \frac{11}{13} . \frac{- 1}{2} + \frac{11}{13} . \frac{- 1}{3} + \frac{11}{13} . \frac{- 1}{6} = \frac{11}{13} . (\frac{- 1}{2} + \frac{- 1}{3} + \frac{- 1}{6}) = \frac{11}{13} . (- 1) = - \frac{11}{13} .$

Bài 2:

a) Cho $Δ A B C$ biết số đo các góc $\hat{A}, \hat{B}, \hat{C}$ biết số đo các góc $\hat{A}, \hat{B}, \hat{C}$ tỉ lệ nghịch với 3 ; 8; 6

Vì $\hat{A}, \hat{B}, \hat{C}$ tỉ lệ nghịch với 3 ; 8; 6 nên $3 \hat{A} = 8 \hat{B} = 6 \hat{C}$

$\begin{array}{l} \Rightarrow \frac{\hat{A}}{\frac{1}{3}} = \frac{\hat{B}}{\frac{1}{8}} = \frac{\hat{C}}{\frac{1}{6}} = \frac{\hat{A} + \hat{B} + \hat{C}}{\frac{1}{3} + \frac{1}{8} + \frac{1}{6}} = \frac{180^{0}}{\frac{15}{24}} = 288^{0} \\ \Rightarrow \hat{A} = 96^{0}; \hat{B} = 36^{0}; \hat{C} = 48^{0} \end{array}$

b) Cho $Δ A B C$ có $5 \hat{C} = \hat{A} + \hat{B}$ . Tính số đo các góc $\hat{A}, \hat{B}, \hat{C}$ biết $\hat{A} : \hat{B} = 2 : 3$

Vì $\hat{A} : \hat{B} = 2 : 3 \Rightarrow \frac{\hat{A}}{2} = \frac{\hat{B}}{3} = \frac{\hat{A} + \hat{B}}{5} = \frac{5 \hat{C}}{5} = \hat{C} \Rightarrow \hat{A} = 2 \hat{C} v à \hat{B} = 3 \hat{C}$

Lại có : $\hat{A} + \hat{B} + \hat{C} = 180^{0}$

Nên: $2 \hat{C} + 3 \hat{C} + \hat{C} = 180^{0}$ $\Rightarrow 6 \hat{C} = 180^{0}$ $\Rightarrow \hat{C} = 30^{0}$

$\Rightarrow \hat{A} = 60^{0}; \hat{B} = 90^{0}; \hat{C} = 30^{0}$

a) Bài 3: Đồ thị hàm số qua điểm $A (1; 3)$ nên ta có:

$3 = (\frac{1}{3} - a) .1$

$\Leftrightarrow a = - \frac{8}{3}$

Vậy công thức của hàm số có dạng $y = 3 x$ .

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Tài liệu có 4 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

toán 7 ôn tập chương I ôn tập chương 2 Các trường hợp bằng nhau của tam giác vuông

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm