Phiếu bài tập tuần 16

Phiếu bài tập tuần 16 - Toán 7

Quý Lê Xuân Ngày: 08-03-2024 Lớp 7

Tải xuống 5 1.5 K 8

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập Phiếu bài tập tuần 16 - Toán 7, tài liệu bao gồm 5 trang, tuyển chọn các bài tập có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Phiếu bài tập tuần 16 - Toán 7 (ảnh 1)

PHIẾU HỌC TẬP TOÁN 7 TUẦN 16

Đại số 7 : §7: Đồ thị hàm số y = ax ( a ≠ 0)

Hình học 7: Luyện tập (ba trường hợp bằng nhau của tam giác)

Bài 1: a) Vẽ đồ thị hàm số $y = - \frac{3}{4} x .$

b) Cho biết tọa độ các điểm $A (4; - 3); B (1; \frac{3}{4}); C (3; 0) .$
Bằng phép tính hãy xác định xem điểm nào thuộc đồ thị hàm số và biễu diễn điểm đó trên mặt phẳng tọa độ.

c) Tính diện tích tam giác $Δ A O C$

Bài 2: a) Xác định hệ số a biết đồ thị hàm số $y = ax$ đi qua điểm $A (2; \frac{3}{2})$ và vẽ đồ thị của hàm số trên.

b) Những điểm nào sau đây thuộc đồ thị hàm số trên:

$B (4 \sqrt{2}; 3 \sqrt{2});$ $C (- 2; - \frac{3}{2});$ $D (- \frac{8}{3}; 2)$

c) Biết điểm $E (m; - 2)$ ; $F (4 \sqrt{3}; b)$ thuộc đồ thị hàm số trên. Tính giá trị của

Bài 3: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD.

a) Chứng minh: AD = BC.

b) Gọi E là giao điểm AD và BC. Chứng minh OE là tia phân giác của góc xOy

Bài 4: Cho tam giác ABC có các góc đều nhọn, và AB < AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.

a, Chứng minh AB = AF.

b, Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // KF.

c, Chứng minh góc ABC lớn hơn góc C.

Hết

PHẦN HƯỚNG DẪN GIẢI

Bài 1:

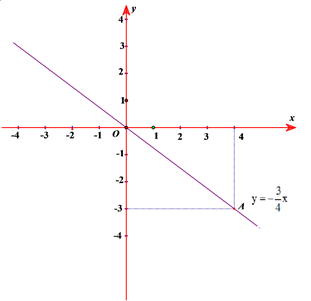
Phiếu bài tập tuần 16 - Toán 7 (ảnh 2)

a) Vẽ đồ thị hàm số $y = - \frac{3}{4} x$

Vẽ hệ trục tọa độ .

Bảng giá trị:

x	0	4
$y = - \frac{3}{4} x$	0	$- 3$

Điểm $A (4; - 3)$ thuộc đồ thị hàm số $y = - \frac{3}{4} x$ . Vậy đường thẳng là đồ thị của hàm số đã cho.

+) Thế $x = 4$ vào hàm số $y = - \frac{3}{4} x$ , ta được: $y = - \frac{3}{4} .4 = - 3$ bằng tung độ điểm A.

Vậy $A (4; - 3)$ thuộc đồ thị hàm số $y = - \frac{3}{4} x$

+) Thế $x = 1$ vào hàm số $y = - \frac{3}{4} x$ , ta được: $y = - \frac{3}{4} .1 = - \frac{3}{4}$ khác tung độ điểm B.

Vậy $B (1; \frac{3}{4})$ không thuộc đồ thị hàm số $y = - \frac{3}{4} x$

+) Thế $x = 3$ vào hàm số $y = - \frac{3}{4} x$ , ta được: $y = - \frac{3}{4} .3 = - \frac{9}{4}$ khác tung độ điểm C.

Vậy $C (3; 0)$ không thuộc đồ thị hàm số $y = - \frac{3}{4} x$ .

c)Tính diện tích tam giác $Δ A O C$

Kẻ đường cao AD của $Δ A B C$ $\Rightarrow x_{D} = 4; y_{D} = 0$

$\Rightarrow D (4; 0)$ thuộc trục Ox. Ta có: $S_{Δ A O C} = \frac{1}{2} . O C . A D = \frac{1}{2} .3.3 = \frac{9}{2}$ (đvdt).

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Tài liệu có 5 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm