Phiếu bài tập tuần 13

Phiếu bài tập tuần 13 - Toán 7

Quý Lê Xuân Ngày: 08-03-2024 Lớp 7

Tải xuống 5 3.1 K 25

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập Phiếu bài tập tuần 13 - Toán 7, tài liệu bao gồm 5 trang, tuyển chọn các bài tập có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Phiếu bài tập tuần 13 - Toán 7 (ảnh 1)

PHIẾU HỌC TẬP TOÁN 7 TUẦN 13

Đại số 7 : § 3: Đại lượng tỉ lệ nghịch

Hình học 7: § 4:Trường hợp bằng nhau thứ hai của tam giác c-g-c

Bài 1: Với cùng một số tiền để mua 225m vải loại 1 có thể mua được bao nhiêu m vải loại 2; biết rằng giá tiền vải loại 2 chỉ bằng 75% giá tiền vải loại 1

Bài 2: Cho 3 đại lượng x, y, z. Hãy cho biết mối liên hệ giữa hai đại lượng x và x biết:

a) x và y tỉ lệ nghịch; y và z tỉ lệ nghịch

b) x và y tỉ lệ nghịch; y và z tỉ lệ thuận

Bài 3: Các giá trị của 2 đại lượng x, y được cho trong bảng có phải là 2 đại lượng tỉ lệ nghịch không? Nếu có, hãy tìm hệ số tỉ lệ và biểu diễn y theo x

x	$- 3$	$- 2$	4	9	15
y	30	45	-22,5	10	-6

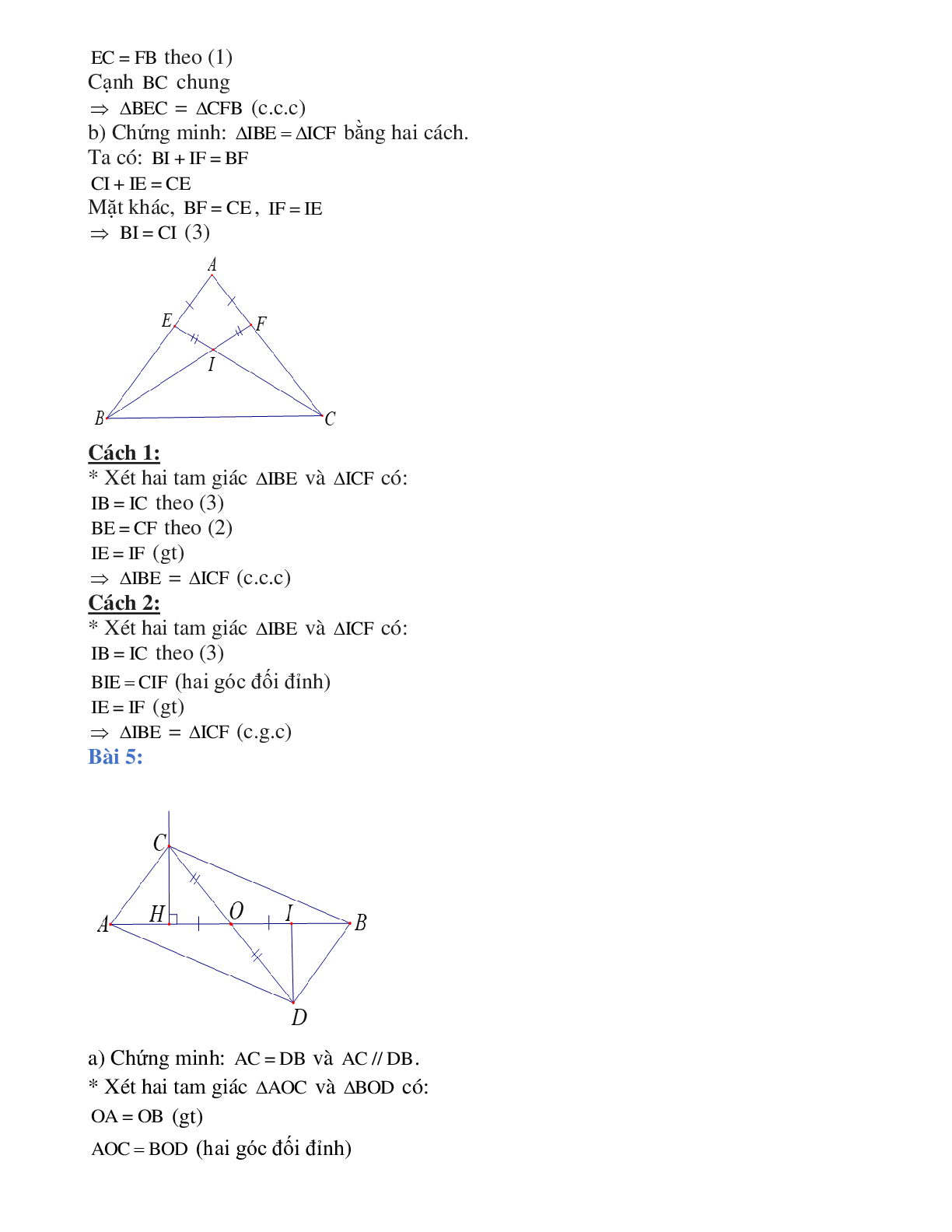
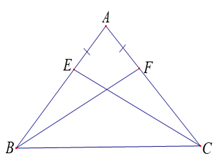
Bài 4: Cho $Δ ABC$ có $AB = AC$ . Lấy điểm E trên cạnh AB, F trên cạnh AC sao cho $AE = AF$ .

a) Chứng minh: $BF = CE$ và $Δ BEC = Δ CFB$ .

b) BF cắt CE tại I, cho biết $IE = IF$ . Chứng minh: $Δ IBE = Δ ICF$ bằng hai cách.

Bài 5: Cho hai đoạn thẳng và cắt nhau tại trung điểm của mỗi đoạn thẳng.

a) Chứng minh: $AC = DB$ và $AC // DB$ .

b) Chứng minh: $AD = CB$ và $AD // CB$ .

c) Chứng minh: $\hat{ACB} = \hat{BDA}$ .

d) Vẽ $CH ⊥ AB$ tại H. Trên tia đối của tia lấy điểm I sao cho $OI = OH$ . Chứng minh: $DI ⊥ AB.$

Bài 6: Cho $Δ MNP$ có $PM = PN$ . Chứng minh: $\hat{PMN} = \hat{PNM}$ bằng hai cách.

PHẦN HƯỚNG DẪN GIẢI

Bài 1:

Với số tiền không đổi thì số m vải mua được và giá vải là hai đại lượng tỉ lệ nghịch

Gọi số m vải loại 2 mua được là x, theo tính chất của đại lượng tỉ lệ nghịch, ta có

$\frac{225}{x} = \frac{75}{100} \Rightarrow x = \frac{225.100}{75} = 300$

Số mét vải loại 2 mua được là 300m.

Bài 2: a) x và y tỉ lệ nghịch $\Rightarrow x y = a$ $(a \neq 0)$

y và z tỉ lệ nghịch $\Rightarrow y z = b \Rightarrow y = \frac{b}{z}$ $(b \neq 0)$

Thay $y = \frac{b}{z}$ ta có $x . \frac{b}{z} = a \Rightarrow x = \frac{a}{b} z$

Vậy x và z là hai đại lượng tỉ lệ thuận theo hệ số $\frac{a}{b}$

b) x và y tỉ lệ nghịch $\Rightarrow x y = a$ $(a \neq 0)$

y và z tỉ lệ thuận $\Rightarrow y = k z$ $(k \neq 0)$

Thay $y = k z$ ta có $x . k z = a \Rightarrow x z = \frac{a}{k}$

Vậy x và z là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ $\frac{a}{k}$

Bài 3: Hai đại lượng x và y cho trong bảng là hai đại lượng tỉ lệ nghịch vì; $- 3.30 = (- 2) .45 = 4. (- 22, 5) = (- 9) .10 = 15. (- 6) = - 90$

hệ số tỉ lệ $a = - 90$ và biểu diễn y theo x là: $y = \frac{- 90}{x}$

Bài 4:

a) Chứng minh: $BF = CE$ và $Δ BEC = Δ CFB$ .

* Xét hai tam giác $Δ BAF$ và $Δ CAE$ có:

$BA = CA$ (gt)

$\hat{A}$ chung

$AF = AE$ (gt)

=> $Δ BAF$ = $Δ CAE$ (c.g.c)

=> $BF = CE$ (1)

Ta có: $AE + EB = AB$

$AF + FC = AC$

Mà $AB = AC$ , $AE = AF$

$EB = FC$ (2)

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Tài liệu có 5 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

toán 7 Đại lượng tỉ lệ nghịch Bài toán về đại lượng tỉ lệ nghịch trường hợp bằng nhau cạnh - góc - cạnh

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm