Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ sách Kết nối tri thức. Bài viết gồm 21 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 2: Cộng, trừ, nhân, chia số hữu tỉ. Mời các bạn đón xem:

Bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

A. Bài tập Cộng, trừ, nhân, chia số hữu tỉ

A1. Bài tập tự luận

Bài 1. Tính giá trị của các biểu thức sau:

a) $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$;

b) $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$;

c) $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$;

d) $3-\frac{1-\frac{1}{7}}{1+\frac{1}{7}}$.

Hướng dẫn giải

a) $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$

$=7+3\frac{1}{4}-\frac{3}{5}+0,4-5-4\frac{1}{4}+1$

$=\left(7-5+1\right)+\left(3\frac{1}{4}-4\frac{1}{4}\right)+\left(-\frac{3}{5}+0,4\right)$

$=3+\left(-1\right)+\left(-0,6+0,4\right)$

$=2+\left(-0,2\right)=1,8$

b) $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$

$=\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{4}{8}+\frac{3}{8}\right)\right]$

$=\frac{2}{3}-\left[\left(-\frac{14}{8}\right)-\frac{7}{8}\right]$

$=\frac{2}{3}-\left(-\frac{21}{8}\right)$

$=\frac{2}{3}+\frac{21}{8}$

$=\frac{16}{24}+\frac{63}{24}=\frac{79}{24}$

c) $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$

$=\left(\frac{36}{4}-\frac{2}{4}-\frac{3}{4}\right):\left(\frac{56}{8}-\frac{2}{8}-\frac{5}{8}\right)$

$=\frac{31}{4}:\frac{49}{8}=\frac{31}{4}\cdot \frac{8}{49}=\frac{62}{49}$

d) $\left(1+\frac{1}{7}\right)=3-\frac{6}{7}:\frac{8}{7}=3-\frac{6}{7}\cdot \frac{7}{8}=3-\frac{3}{4}=\frac{12}{4}-\frac{3}{4}=\frac{9}{4}$.

Bài 2. Tính:

a) $\frac{-8}{18}+\frac{15}{27}$;

b) $3,5-\left(-\frac{2}{7}\right)$;

c) $-0,25\cdot \left(-0,4\right)$;

d) $-6:3\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-8}{18}+\frac{15}{27}=\frac{-4}{9}+\frac{5}{9}=\frac{1}{9}$;

b) $3,5-\left(-\frac{2}{7}\right)=\frac{7}{2}+\frac{2}{7}=\frac{49}{14}+\frac{4}{14}=\frac{53}{14}$;

c) $-0,25\cdot \left(-0,4\right)=0,25\cdot 0,4=0,1$

d) $-6:3\frac{1}{5}=-6:\frac{16}{5}=-6\cdot \frac{5}{16}=\frac{-15}{8}$.

Bài 3.Tính: $\frac{3}{5}+\frac{-1}{3}$

Hướng dẫn giải

$\frac{3}{5}+\frac{-1}{3}=\frac{9}{15}+\frac{-5}{15}=\frac{9-5}{15}=\frac{4}{15}$

Bài 4. Viết số hữu tỉ $\frac{-7}{12}$dưới các dạng sau đây:

a) $\frac{-7}{12}$ là tổng của hai số hữu tỉ âm.

b) $\frac{-7}{12}$ là hiệu của hai số hữu tỉ dương.

Hướng dẫn giải

a) $\frac{-7}{12}$ là tổng của hai số hữu tỉ âm là: $\frac{-7}{12}=\frac{-1}{6}+\frac{-5}{12}$  vì

$\frac{-2}{12}+\frac{-5}{12}=\frac{-1}{6}+\frac{-5}{12}=\frac{-7}{12}$

b) $\frac{-7}{12}$ là hiệu của hai số hữu tỉ dương là:$\frac{-7}{12}=1-\frac{19}{12}$ vì

$\frac{12}{12}-\frac{19}{12}=1-\frac{19}{12}=\frac{-7}{12}$

Bài 5. Tìm x biết:

a) x + $\frac{2}{3}=\frac{4}{5}$ 

b) x - $\frac{1}{15}=\frac{1}{10}$

Hướng dẫn giải

a) x + $\frac{2}{3}=\frac{4}{5}$

    x         = $\frac{4}{5}-\frac{2}{3}$

    x         = $\frac{2}{15}$ 

  Vậy x = $\frac{2}{15}$ là giá trị cần tìm.                                                   

b) x - $\frac{1}{15}=\frac{1}{10}$

    x          = $\frac{1}{10}+\frac{1}{15}$

   x           = $\frac{1}{6}$

Vậy x = $\frac{1}{6}$ là giá trị cần tìm.

A2. Bài tập trắc nghiệm

Bài 3. Giá trị của biểu thức $\frac{3}{5}-\left(\frac{1}{2}-\frac{2}{5}\right)$ là

A. $\frac{-3}{10}$;

B. $\frac{1}{2}$;

C. $\frac{3}{2}$;

D. $\frac{7}{10}$.

Hướng dẫn giải

Đáp án đúng là: B

$\frac{3}{5}-\left(\frac{1}{2}-\frac{2}{5}\right)$ = $\frac{3}{5}-\frac{1}{2}+\frac{2}{5}$ = $\left(\frac{3}{5}+\frac{2}{5}\right)-\frac{1}{2}$ = $1-\frac{1}{2}$ = $\frac{1}{2}$.

Bài 4. Ngăn đựng sách của một giá sách trong thư viện dài 120 cm (xem hình dưới). Người ta dự định xếp các cuốn sách dày khoảng 2,5 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?

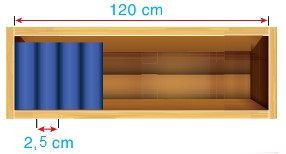
A. 50 cuốn sách;

B. 48 cuốn sách;

C. 40 cuốn sách;

D. 25 cuốn sách.

Hướng dẫn giải

Đáp án đúng là: B

Ngăn sách đó có thể để được nhiều nhất số cuốn sách như thế là:

120 : 2,5 = 48 (cuốn sách).

Bài 5. Giá trị của biểu thức $6,25+\left[1,75-\left(0,75-2,75\right)\right]$ là

A. 6;

B. 6,5;

C. 9,5;

D. 10.

Hướng dẫn giải

Đáp án đúng là: D

$6,25+\left[1,75-\left(0,75-2,75\right)\right]$ 

= $6,25+\left[1,75-0,75+2,75\right]$ 

= $6,25+1,75-0,75+2,7$

= $\left(6,25+2,75\right)+\left(1,75-0,75\right)$

= 9 + 1

= 10

B. Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ

1. Cộng và trừ hai số hữu tỉ

Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ 1: Tính:

a) $\frac{-6}{18}+\frac{18}{27};$

b) – 0,32 + 0,98;

c) – 5 + $2\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-6}{18}+\frac{18}{27}=\frac{-1}{3}+\frac{2}{3}=\frac{-1+2}{3}=\frac{1}{3};$

b) – 0,32 + 0,98 = 0,98 – 0,32 = 0,66;

c) – 5 + $2\frac{1}{5}$ = $-\frac{25}{5}+\frac{11}{5}=\frac{-25+11}{5}=\frac{-14}{5}.$

Chú ý:

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.

• Trong phép cộng trừ với số hữu tỉ $\mathrm{\mathbb{Q}}$, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên $\mathrm{\mathbb{Z}}$.

• Đối với một tổng trong $\mathrm{\mathbb{Q}}$, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong $\mathrm{\mathbb{Z}}$.

• Hai số đối nhau luôn có tổng bằng 0:

a + (– a) = 0.

Ví dụ 2: Thực hiện phép tính

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$;

b) $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$.

Hướng dẫn giải

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$

$=\frac{-2}{3}+\frac{-5}{6}+\frac{1}{3}+\frac{7}{6}$  (Viết số hữu tỉ dưới dạng phân số có mẫu dương)

$=\frac{-2}{3}+\frac{1}{3}+\frac{-5}{6}+\frac{7}{6}$             (Tính chất giao hoán)

$=\left(\frac{-2}{3}+\frac{1}{3}\right)+\left(\frac{-5}{6}+\frac{7}{6}\right)$      (Tính chất kết hợp)

$=\frac{-1}{3}+\frac{2}{6}$

$=\frac{-1}{3}+\frac{1}{3}=0$                       (Tổng hai số đối nhau bằng 0)

b)  $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$

$=\frac{31}{3}-\frac{1}{2}-\frac{2}{3}+\frac{1}{2}$                  (Quy tắc bỏ dấu ngoặc có dấu “–” đằng trước)

$=\left(\frac{31}{3}-\frac{2}{3}\right)+\left(-\frac{1}{2}+\frac{1}{2}\right)$         (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)

$=\frac{29}{3}+0=\frac{29}{3}$                       (Cộng với số 0)

2. Nhân và chia hai số hữu tỉ

• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Chú ý:

• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.

Ví dụ 1: Tính:

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$;

b) $-\frac{7}{6}:1\frac{5}{7}$;

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$.

Hướng dẫn giải

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$

$=\frac{23}{3}\cdot \frac{3}{23}\cdot \left(-\frac{9}{10}\right)$

$=1\cdot \left(-\frac{9}{10}\right)=-\frac{9}{10}$                (Nhân với số 1)

b) $-\frac{7}{6}:1\frac{5}{7}$

$=-\frac{7}{6}:\frac{12}{7}$

$=-\frac{7}{6}\cdot \frac{7}{12}=-\frac{49}{72}$

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$

$=\frac{7}{6}\cdot \left[3\frac{1}{4}+\left(-0,25\right)\right]$

$=\frac{7}{6}\cdot \left(\frac{13}{4}+\frac{-1}{4}\right)$

$=\frac{7}{6}\cdot \frac{12}{4}=\frac{7}{2}$

Ví dụ 2: 1,25 . (– 4,6) = – (1,25 . 4,6) = – 5,75.

A. Phương pháp giải

1. Với $x=\frac{a}{m},y=\frac{b}{m}\left(a,b,m\in Z,m>0\right)$ ta có:

.$x+y=\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m};x-y=\frac{a}{m}-\frac{b}{m}=\frac{a-b}{m}$

2. Với $x=\frac{a}{b};y=\frac{c}{d}$ ta có:

$x.y=\frac{a}{b}.\frac{c}{d}=\frac{ac}{bd};x:y=\frac{a}{b}:\frac{c}{d}=\frac{a.d}{b.c}$ (với $y\ne 0$).

3. Các phép toán trong Q cũng có những tính chất giao hoán, kết hợp và phân phối của phép nhân đối với phép cộng như trong tập hợp Z. Ngoài ra các quy tắc bỏ dấu ngoặc, quy tắc chuyển vế cũng như trong tập hợp Z.

B. Một số ví dụ

Ví dụ 1. Thực hiện các phép tính:

a) $\frac{1}{18}-\left(-\frac{1}{9}-\frac{1}{6}-\frac{1}{3}\right)$;                                  

b) $\frac{1}{2}-\frac{-1}{3}+\frac{1}{23}+\frac{1}{6}$;

Giải

Tìm cách giải. Khi thực hiện các phép tính chỉ có phép cộng và trừ, ta có thể thực hiện trong ngoặc trước, thực hiện từ trái qua phải. Tuy nhiên nếu có nhiều dấu (-) ta có thể giảm bớt dấu (-) bằng cách bỏ ngoặc. Ngoài ra có thể dùng tính chất giao hoán và kết hợp nhằm giải bài toán được nhanh hơn.

Trình bày lời giải.

a) $\frac{1}{18}-\left(-\frac{1}{9}-\frac{1}{6}-\frac{1}{3}\right)=\frac{1}{18}+\frac{1}{9}+\frac{1}{6}+\frac{1}{3}=\frac{1}{18}+\frac{2}{18}+\frac{3}{18}+\frac{6}{18}=\frac{12}{18}=\frac{2}{3};$

b) $\frac{1}{2}-\frac{-1}{3}+\frac{1}{23}+\frac{1}{6}=\frac{1}{2}+\frac{1}{3}+\frac{1}{23}+\frac{1}{6}=\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\right)+\frac{1}{23}=1+\frac{1}{23}=1\frac{1}{23}$

Ví dụ 2. Thực hiện các phép tính

a) $\left(\frac{1}{2}-\frac{13}{14}\right):\frac{5}{7}-\left(-\frac{2}{21}+\frac{1}{7}\right):\frac{5}{7}$;                    

b) $\left(-\frac{3}{4}+\frac{5}{13}\right):\frac{2}{7}-\left(2\frac{1}{4}-\frac{8}{13}\right):\frac{2}{7}$

Giải

Tìm cách giải. Vì phép chia là phép nhân số bị chia với số nghịch đảo của số chia nên ta có thể vận dụng tính chất phân phối:

$a:m+b:m=\left(a+b\right):m$

$a:m-b:m=\left(a-b\right):m$

Trình bày lời giải

a) $\left(\frac{1}{2}-\frac{13}{14}+\frac{2}{21}-\frac{1}{7}\right):\frac{5}{7}=-\frac{10}{21}.\frac{7}{5}=\frac{-2}{3}$

b) $\left(-\frac{3}{4}+\frac{5}{13}-2\frac{1}{4}+\frac{8}{13}\right):\frac{2}{7}=\left(-2\right).\frac{7}{2}=-7$

Ví dụ 3. Tìm x.

a) $\frac{1}{2}x+\frac{3}{5}x=\frac{-3}{65}$;         

b) $\left(\frac{2}{9}x-\frac{4}{9}\right)\left(\frac{1}{3}+\frac{-4}{7}:x\right)=0$;

c) $\frac{x+5}{2015}+\frac{x+6}{2014}+\frac{x+7}{2013}+\frac{x+8}{2012}+\frac{x+9}{2011}=-5$;

d) $\frac{x+2}{338}+\frac{x+3}{337}+\frac{x+4}{336}+\frac{x+5}{335}+\frac{x+360}{5}=0$.

Giải

Tìm cách giải. Khi tìm x ta có thể vận dụng các tính chất sau:

·$ax+bx=\left(a+b\right)x$       

·$\frac{k}{a}=k.\frac{1}{a}$ nên $\frac{k}{a}+\frac{k}{b}+\frac{k}{c}=k.\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)$

·$A.B=0$ thì $A=0$ hoặc $B=0$

Trình bày lời giải.

a) $\frac{1}{2}x+\frac{3}{5}x=\frac{-3}{65}\iff \left(\frac{1}{2}+\frac{3}{5}\right).x=\frac{-3}{65}\Rightarrow \frac{11}{10}.x=\frac{-3}{65}\Rightarrow x=\frac{-3}{65}:\frac{11}{10}$

$\Rightarrow x=\frac{-6}{143}$

b) $\left(\frac{2}{9}x-\frac{4}{9}\right)\left(\frac{1}{3}+\frac{-4}{7}:x\right)=0\iff \frac{2}{9}x-\frac{4}{9}=0$ hoặc $\frac{1}{3}+\frac{-4}{7}:x=0$ suy ra $\frac{2}{9}x=\frac{4}{9}$ hoặc $\frac{-4}{7}:x=\frac{-1}{3}\Rightarrow x=2$ hoặc $x=\frac{12}{7}$.

Vậy $x\in \left\{2;\frac{12}{7}\right\}$

c) $\frac{x+5}{2015}+\frac{x+6}{2014}+\frac{x+7}{2013}+\frac{x+8}{2012}+\frac{x+9}{2011}=-5$

<=> $\frac{x}{2015}+\frac{5}{2015}+\frac{x}{2014}+\frac{6}{2014}+\frac{x}{2013}+\frac{7}{2013}+\frac{x}{2012}+\frac{8}{2012}+\frac{x}{2011}+\frac{9}{2011}=-5$

$\iff x(\frac{1}{2015}+\frac{1}{2014}+\frac{1}{2013}+\frac{1}{2012}+\frac{1}{2011})+(\frac{5}{2015}+\frac{6}{2014}+\frac{7}{2013}+\frac{8}{2012}+\frac{9}{2011})=-5$

$\iff x=-2020$