Với giải Thực hành 5 trang 85 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 1: Khái niệm vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 1: Khái niệm vecto
Thực hành 5 trang 85 Toán lớp 10: Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
a) Tìm các vectơ bằng vectơ .
b) Tìm các vectơ đối vectơ
Phương pháp giải:
a)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ
Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ
b)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ
Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ
Lời giải:
Từ giả thiết ta có:
; ;
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ là và
b) Các vectơ đối vectơ là và
Lý thuyết Vectơ bằng nhau – Vectơ đối nhau
Hai vectơ và được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu .
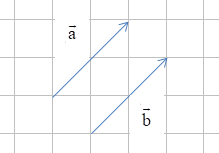
Hai vectơ và được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu . Khi đó vectơ được gọi là vectơ đối của vectơ .
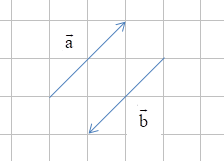
Chú ý:
+ Cho vectơ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho . Khi đó độ dài của là độ dài đoạn thẳng OA, kí hiệu là .
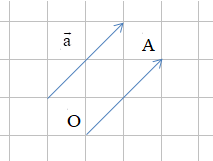
+ Cho đoạn thẳng MN, ta luôn có .
Ví dụ: Cho hình bình hành ABCD. Tìm các cặp vectơ bằng nhau và các cặp vectơ đối nhau.
Hướng dẫn giải
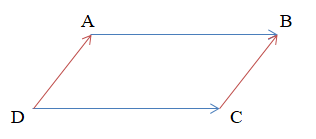
+ Các cặp vectơ bằng nhau:
Vì ABCD là hình bình hành nên ta có AB // DC và AB = DC (tính chất hình bình hành)
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
Tương tự, vì ABCD là hình bình hành nên ta có AD // BC và AD = BC.
Mà hai vectơ cùng hướng và hai vectơ cùng hướng.
Do đó và .
Vậy ta có 4 cặp vectơ bằng nhau là: , , và .
+ Các cặp vectơ đối nhau:
Vì ABCD là hình bình hành nên ta có AB // DC và AB = DC (tính chất hình bình hành)
Mà hai vectơ ngược hướng và hai vectơ ngược hướng.
Do đó và .
Tương tự, vì ABCD là hình bình hành nên ta có AD // BC và AD = BC.
Mà hai vectơ ngược hướng và hai vectơ ngược hướng.
Do đó và .
Vậy ta có 4 cặp vectơ đối nhau là: , , và .
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 3 trang 84 Toán lớp 10: Quan sát Hình 8 và gọi tên các vectơ:...
Thực hành 4 trang 84 Toán lớp 10: Khẳng định sau đây đúng hay sai? Hãy giải thích...
Thực hành 6 trang 86 Toán lớp 10: Tìm độ dài của các vectơ trong Ví dụ 5...
Bài 1 trang 86 Toán lớp 10: a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:...
Bài 3 trang 86 Toán lớp 10: Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16)...
Bài 6 trang 87 Toán lớp 10: Gọi O là tâm hình lục giác đều ABCDEF...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vecto
Bài 3: Tích của một số với một vecto
Bài 4: Tích vô hướng của hai vecto