Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương 4 chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài tập cuối chương 4
Video bài giảng Bài tập cuối chương 4 - Chân trời sáng tạo
Giải toán lớp 10 trang 78 Tập 1 Chân trời sáng tạo
Bài 1 trang 78 Toán lớp 10: Cho tam giác ABC. Biết a = 49,4; b = 26,4; . Tính hai góc và cạnh c.
Phương pháp giải:
Bước 1: Tính cạnh c: Áp dụng định lí cosin:
Bước 2: Tính hai góc : Áp dụng định lí sin:
Lời giải:
Áp dụng định lí cosin trong tam giác ABC, ta có:
Áp dụng định lí sin, ta có:
Bài 2 trang 78 Toán lớp 10: Cho tam giác ABC. Biết a = 24, b = 13, c = 15. Tính các góc .
Phương pháp giải:
Áp dụng hệ quả của định lí cosin:
Từ đó suy ra các góc
Lời giải:
Áp dụng hệ quả của định lí cosin, ta có:
Bài 3 trang 78 Toán lớp 10: Cho tam giác ABC có a = 8, b = 10, c = 13.
a) Tam giác ABC có góc tù không?
b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.
c) Lấy điểm D đối xứng với A qua C. Tính độ dài BD.
Lời giải:
a) Áp dụng hệ quả của định lí cosin, ta có:
, tam giác ABC có góc C tù.
b)
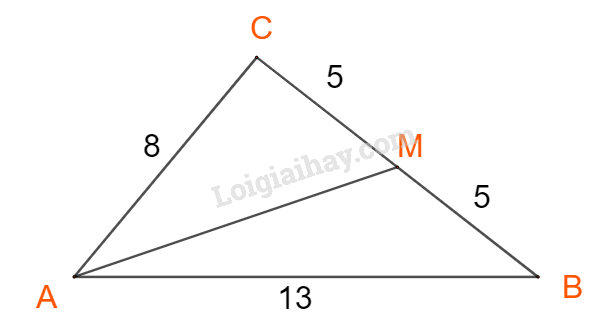
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
+) Ta có: .
Áp dụng công thức heron, ta có:
+) Áp dụng định lí sin, ta có:
c)
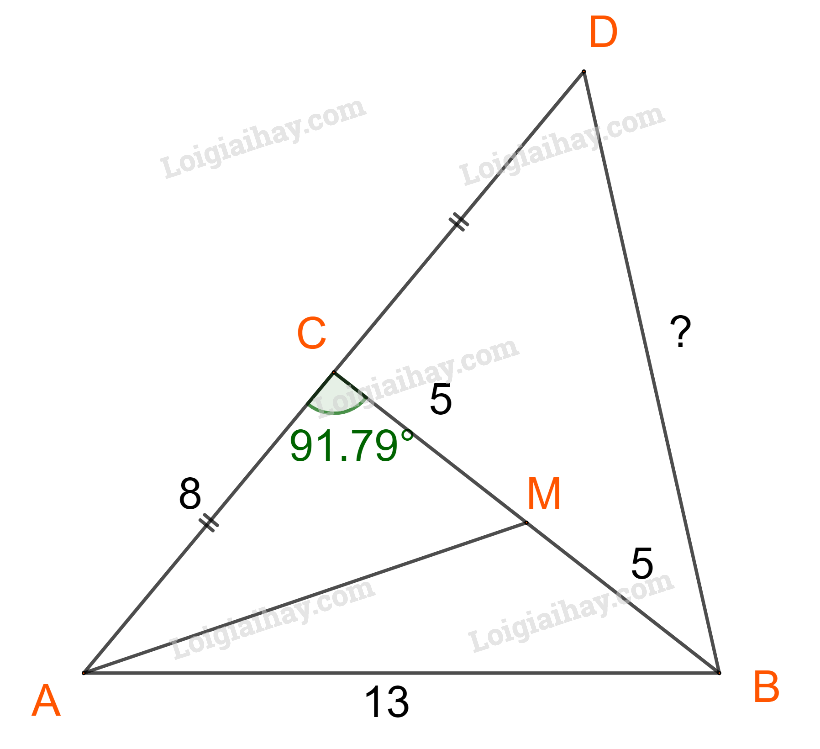
Ta có: ;
Áp dụng định lí cosin trong tam giác BCD, ta có:
Giải toán lớp 10 trang 79 Tập 1 Chân trời sáng tạo
Bài 4 trang 79 Toán lớp 10: Cho tam giác ABC có , b = 8, c = 5. Tính:
a) Cạnh a và các góc , ;
b) Diện tích tam giác ABC;
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Lời giải:
a) Áp dụng định lí cosin, ta có:
Áp dụng định lí sin, ta có:
b) Diện tích tam giác ABC là:
S = =
c)
+) Theo định lí sin, ta có:
+) Đường cao AH của tam giác bằng:
Bài 5 trang 79 Toán lớp 10: Cho hình bình hành ABCD.
a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
b) Cho AB = 4, BC = 5, BD = 7. Tính AC.
Phương pháp giải:
a) Bước 1. Tính góc AC, BD theo AB, BC, cosA dựa vào định lí cosin
Bước 2: Biến đối để suy ra đẳng thức
b) Theo câu a: , từ đó suy ra AC.
Lời giải:
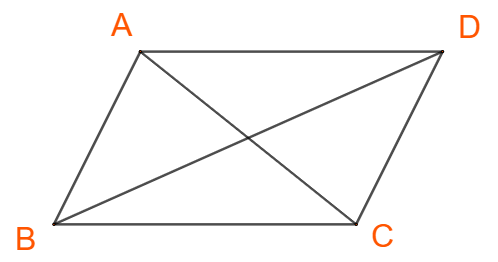
a) Áp dụng định lí cosin ta có:
Mà
b) Theo câu a, ta suy ra:
Bài 6 trang 79 Toán lớp 10: Cho tam giác ABC có a = 15, b = 20, c = 25.
a) Tính diện tích tam giác ABC.
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Phương pháp giải:
a) Áp dụng công thức heron: với
b) Áp dụng công thức:
Lời giải:
a) Ta có:
Áp dụng công thức heron, ta có:
b) Ta có:
Bài 7 trang 79 Toán lớp 10: Cho tam giác ABC. Chứng minh rằng:
cotA + cotB + cotC =
Phương pháp giải:
Tính bằng cách: Áp dụng hệ quả của định lí sin và định lí cosin:
;
Lời giải:
Áp dụng hệ quả của định lí sin và định lí cosin, ta có:
và
Tương tự ta có: và
Phương pháp giải:
Áp dụng định lí cosin:
Lời giải:
Áp dụng định lí cosin, ta có:
Vậy khoảng cách giữa hai tòa nhà là 23,96 km.
Phương pháp giải:
Bước 1: Tính AB theo QB, dựa vào tan góc P và Q.
Bước 2: Lập phương trình, tìm QB.
Bước 3: Tính AB:
Lời giải:
Xét tam giác APB và AQB, ta có:
và
Mà
Vậy tháp hải đăng cao khoảng 568,5 m.
Phương pháp giải:
Bước 1: Tính góc => Áp dụng định lí sin trong tam giác để tính
Bước 2: Tính từ đó suy ra chiều cao của tháp.
Lời giải:
Ta có:
Áp dụng định lí sin trong tam giác , ta có:
Áp dụng định lí sin trong tam giác , ta có:
Do đó, chiều cao CD của tháp là:
Lý thuyết Chương 4: Hệ thức lượng trong tam giác
1. Giá trị lượng giác
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
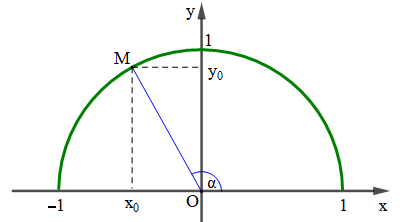
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho . Gọi (; ) là toạ độ điểm M, ta có:
- Tung độ của M là sin của góc α, kí hiệu là sinα = ;
- Hoành độ của M là côsin của góc α, kí hiệu là cosα = ;
- Tỉ số ( ≠ 0) là tang của góc α, kí hiệu là
- Tỉ số ( ≠ 0) là côtang của góc α, kí hiệu là
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.
Ví dụ 1. Tìm các giá trị lượng giác của góc 150°.
Hướng dẫn giải
Lấy điểm M trên nửa đường tròn đơn vị sao cho
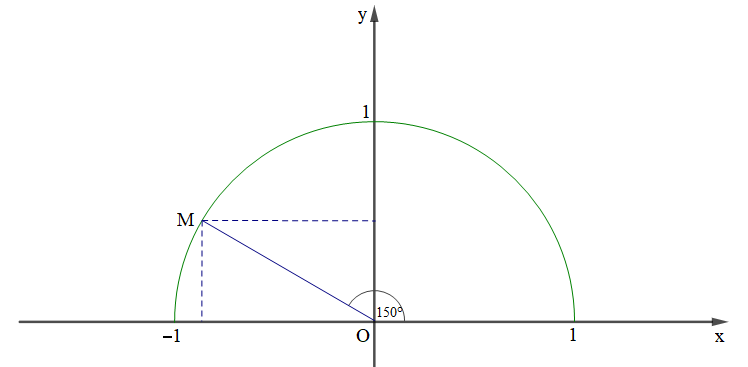 Ta có: .
Ta có: .
Khi đó ta tính được toạ độ của điểm M là
Theo định nghĩa ta có:
Chú ý:
a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.
Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
b) tanα chỉ xác định khi α ≠ 90°.
cotα chỉ xác định khi α ≠ 0° và α ≠ 180°.
Ví dụ 2. Với α = 30° thì sinα > 0, cosα > 0, tanα > 0 và cotα > 0.
Với α = 150° (như trong Ví dụ 1) thì sinα > 0, cosα < 0, tanα < 0 và cotα < 0.
2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Ví dụ 3.
a) Biết . Tính cos30°, cos150°, sin120°.
b) Biết tan45° = 1. Tính tan135°.
Hướng dẫn giải
a) Ta có:
Suy ra:
(vì 30° và 60° là hai góc phụ nhau);
(vì 150° và 30° là hai góc bù nhau);
(vì 120° và 60° là hai góc bù nhau);
b) Ta có: tan45° = 1.
Suy ra:
tan135° = tan(180° ‒ 45°) = ‒tan45° = ‒1 (vì 135° và 45° là hai góc bù nhau);
3. Giá trị lượng giác của một số góc đặc biệt
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt: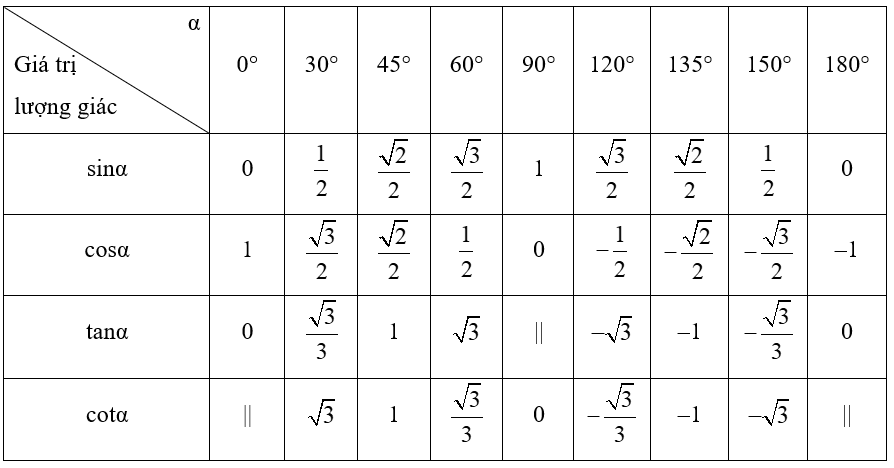 Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Ví dụ 4. Tính giá trị các biểu thức sau:
a) A = .sin90° + .cos90° + .cos180°;
b) B = 3 – 135° + 2120° ‒ 3150°.
Hướng dẫn giải
a) A =.sin90° + .cos90° + .cos180°
A = . 1+ .0 +.(‒1)
A = ‒ .
b) B = 3 – sin2 135° + 2cos2 120° ‒ 3tan2 150°
B = 2.
Ví dụ 5. Tìm góc α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) ;
b) cosα = ‒1;
c) tanα = 0;
d)
Hướng dẫn giải
a) Ta có: α = 45° hoặc α = 135°.
b) cosα = ‒1α = 180°.
c) tanα = 0α = 0° hoặc α = 180°.
d) α = 120°.
4. Sử dụng máy tính cầm tay về tính giá trị lượng giác của một góc
Có nhiều loại máy tính cầm tay có thể giúp tính nhanh chóng giá trị lượng giác của một góc.
Chẳng hạn, ta có thể thực hiện trên một loại máy tính cầm tay như sau:
Sau khi mở máy, ẩn liên tiếp các phím để màn hình hiện lên bảng lựa chọn.

Ấn phím để vào chế độ cài đặt đơn vị đo góc.

Ấn tiếp phím để xác định đơn vị đo góc là “độ”.
Ấn các phím để vào chế độ tính toán như hình ảnh dưới đây:
4.1. Tính các giá trị lượng giác của góc
Ví dụ 6. Sử dụng máy tính cầm tay, tính sin125°, cos50°12', tan160°56'25'', cot100°.
Hướng dẫn giải
- Để tính sin125°, ta bấm liên tiếp các phím sau đây
:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy sin125° ≈ 0,81915204429.
- Để tính cos50°12', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cos50°12' ≈ 0,64010969948.
- Để tính tan160°56'25'', ta bấm liên tiếp các phím sau đây: 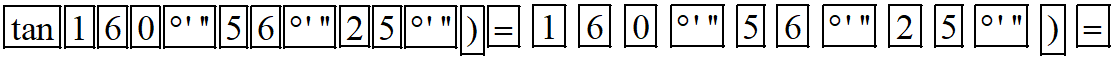 Khi đó ta được kết quả hiện trên màn hình là:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy tan160°56'25'' ≈ ‒0,345493396426.
- Để tính cot100°, ta bấm liên tiếp các phím sau đây:  Khi đó ta được kết quả hiện trên màn hình là:
Khi đó ta được kết quả hiện trên màn hình là:

Vậy cot100° ≈ ‒0,17632698071.
4.2. Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Ví dụ 7. Sử dụng máy tính cầm tay, tìm α (0° < α < 180°) biết sinα = 0,51; cosα = ‒0,7; cotα = 1,7.
Hướng dẫn giải
- Để tìm α khi biết sinα = 0,51, ta ấn liên tiếp các phím sau đây:
![]()
Khi đó ta được kết quả hiện trên màn hình là:

Vậy với sinα = 0,51 thì α ≈ 30°39'50''.
Ta đã được học với 0° < α < 180° thì sin(180° ‒ α) = sinα nên ngoài giá trị α ≈ 30°39'50'' thì ta còn có giá trị α ≈ 180° ‒ 30°39'50'' ≈ 149°20'10''.
Ta bấm máy tính như sau:![]() - Để tìm α khi biết cosα = ‒0,7, ta ấn liên tiếp các phím sau đây:
- Để tìm α khi biết cosα = ‒0,7, ta ấn liên tiếp các phím sau đây:![]() Khi đó ta được kết quả hiện trên màn hình là:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cosα = ‒0,7 thì α ≈ 134°25'37''.
- Để tìm α khi biết ta ấn liên tiếp các phím sau đây:![]() Khi đó ta được kết quả hiện trên màn hình là:
Khi đó ta được kết quả hiện trên màn hình là: 
Vậy với thì α ≈ 54°44'8''.
- Để tìm α khi biết cotα = 1,7, trước hết ta tính , ta ấn liên tiếp các phím sau đây:
![]()
Khi đó ta được kết quả hiện trên màn hình là:
Sau đó ta bấm liên tiếp các phím:![]() Khi đó ta được kết quả hiện trên màn hình là:
Khi đó ta được kết quả hiện trên màn hình là:

Vậy với cotα = 1,7 thì α ≈ 30°27'56''.
5. Định lí côsin trong tam giác
Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Từ định lí côsin, ta có hệ quả sau đây:
Hệ quả:
6. Định lí sin trong tam giác
Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
7. Các công thức tính diện tích tam giác
Cho tam giác ABC. Ta kí hiệu:
+) BC = a, CA = b, AB = c.
+) ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.
+) R là bán kính đường tròn ngoại tiếp tam giác.
+) r là bán kính đường tròn nội tiếp tam giác.
+) p là nửa chu vi tam giác.
+) S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
(1)
(2)
(3)
(4) S = pr;
(5) (Công thức Heron).
8. Giải tam giác
Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.
9. Áp dụng giải tam giác vào thực tế
Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Giải tam giác và ứng dụng thực tế