Giải toán 10 trang 79 Tập 1 Chân trời sáng tạo

Lữ Ngọc My My Ngày: 17-02-2023 Lớp 10

425

Với Giải toán 10 trang 79 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 79 Tập 1 Chân trời sáng tạo

Bài 4 trang 79 Toán lớp 10: Cho tam giác ABC có $\hat{A} = 120^{o}$ , b = 8, c = 5. Tính:

a) Cạnh a và các góc $\hat{B}$ , $\hat{C}$ ;

b) Diện tích tam giác ABC;

c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.

Lời giải:

a) Áp dụng định lí cosin, ta có:

$\begin{array}{l} a^{2} = b^{2} + c^{2} - 2 b c . \cos A \\ \Leftrightarrow a^{2} = 8^{2} + 5^{2} - 2.8.5. \cos 120^{\circ} = 129 \\ \Rightarrow a = \sqrt{129} \end{array}$

Áp dụng định lí sin, ta có:

$\begin{array}{l} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \Rightarrow \frac{\sqrt{129}}{\sin 120^{\circ}} = \frac{8}{\sin B} = \frac{5}{\sin C} \\ \Rightarrow {\begin{cases} \sin B = \frac{8. \sin 120^{\circ}}{\sqrt{129}} \approx 0, 61 \\ \sin C = \frac{5. \sin 120^{\circ}}{\sqrt{129}} \approx 0, 38 \end{cases} \Rightarrow {\begin{cases} \hat{B} \approx 37, 59^{\circ} \\ \hat{C} \approx 22, 41^{\circ} \end{cases} \end{array}$

b) Diện tích tam giác ABC là:

S = $\frac{1}{2} b c . \sin A$ = $\frac{1}{2} . 8.5 . \sin 120 ° = 10 \sqrt{3}$

+) Theo định lí sin, ta có: $R = \frac{a}{\sin A} = \frac{\sqrt{129}}{\sin 120^{\circ}} = 2 \sqrt{43}$

+) Đường cao AH của tam giác bằng: $A H = \frac{2 S}{a} = \frac{2.10 \sqrt{3}}{\sqrt{129}} = \frac{20 \sqrt{43}}{43}$

Bài 5 trang 79 Toán lớp 10: Cho hình bình hành ABCD.

a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.

b) Cho AB = 4, BC = 5, BD = 7. Tính AC.

Phương pháp giải:

a) Bước 1. Tính góc AC, BD theo AB, BC, cosA dựa vào định lí cosin

Bước 2: Biến đối để suy ra đẳng thức

b) Theo câu a: $A C^{2} = 2 (A B^{2} + B C^{2}) - B D^{2}$ , từ đó suy ra AC.

Lời giải:

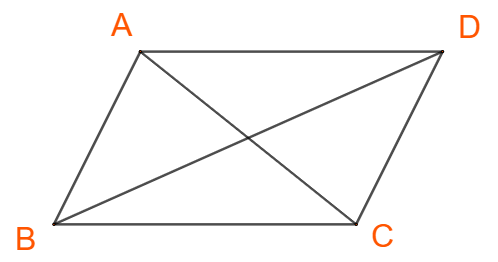
a) Áp dụng định lí cosin ta có:

${\begin{cases} A C^{2} = A B^{2} + B C^{2} - 2. A B . B C . \cos B \\ B D^{2} = A B^{2} + A D^{2} - 2. A B . A D . \cos A \end{cases}$

Mà $A D = B C; \cos A = \cos (180^{\circ} - B) = - \cos B$

$\begin{array}{l} \Rightarrow {\begin{cases} A C^{2} = A B^{2} + B C^{2} + 2. A B . B C . \cos A \\ B D^{2} = A B^{2} + B C^{2} - 2. A B . A D . \cos A \end{cases} \\ \Rightarrow A C^{2} + B D^{2} = 2 (A B^{2} + B C^{2}) \end{array}$

b) Theo câu a, ta suy ra: $A C^{2} = 2 (A B^{2} + B C^{2}) - B D^{2}$

$\begin{array}{l} \Rightarrow A C^{2} = 2 (4^{2} + 5^{2}) - 7^{2} = 33 \\ \Rightarrow A C = \sqrt{33} \end{array}$

Bài 6 trang 79 Toán lớp 10: Cho tam giác ABC có a = 15, b = 20, c = 25.

a) Tính diện tích tam giác ABC.

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Phương pháp giải:

a) Áp dụng công thức heron: $S = \sqrt{p (p - a) (p - b) (p - c)}$ với $p = \frac{a + b + c}{2}$

b) Áp dụng công thức: $S = \frac{a b c}{4 R} \Rightarrow R = \frac{a b c}{4 S}$

Lời giải:

a) Ta có: $p = \frac{a + b + c}{2} = \frac{15 + 20 + 25}{2} = 30$

Áp dụng công thức heron, ta có: $S = \sqrt{30. (30 - 15) . (30 - 20) . (30 - 25)} = 150$

b) Ta có: $S = \frac{a b c}{4 R} \Rightarrow R = \frac{a b c}{4 S} = \frac{15.20.25}{4.150} = 12, 5.$

Bài 7 trang 79 Toán lớp 10: Cho tam giác ABC. Chứng minh rằng:

cotA + cotB + cotC = $\frac{R (a^{2} + b^{2} + c^{2})}{a b c}$

Phương pháp giải:

Tính $\cot A, \cot B, \cot C$ bằng cách: Áp dụng hệ quả của định lí sin và định lí cosin:

$\sin A = \frac{a}{2 R}$ ; $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

Lời giải:

Áp dụng hệ quả của định lí sin và định lí cosin, ta có:

$\frac{a}{\sin A} = 2 R \Rightarrow \sin A = \frac{a}{2 R}$

và $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\Rightarrow \cot A = \frac{\cos A}{\sin A} = \frac{b^{2} + c^{2} - a^{2}}{2 b c} : \frac{a}{2 R} = R . \frac{b^{2} + c^{2} - a^{2}}{a b c}$

Tương tự ta có: $\cot B = R . \frac{a^{2} + c^{2} - b^{2}}{a b c}$ và $\cot C = R . \frac{a^{2} + b^{2} - c^{2}}{a b c}$

$\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{R}{a b c} [(b^{2} + c^{2} - a^{2}) + (a^{2} + c^{2} - b^{2}) + (a^{2} + b^{2} - c^{2})] \\ = \frac{R}{a b c} (2 b^{2} + 2 c^{2} + 2 a^{2} - a^{2} - c^{2} - b^{2}) = \frac{R (a^{2} + b^{2} + c^{2})}{a b c} \end{array}$

Bài 8 trang 79 Toán lớp 10: Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là 2,1°.

Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó

Phương pháp giải:

Áp dụng định lí cosin: $A B^{2} = 370^{2} + 350^{2} - 2.370.350. \cos 2, 1^{\circ}$

Lời giải:

Áp dụng định lí cosin, ta có:

$\begin{array}{l} A B^{2} = 370^{2} + 350^{2} - 2.370.350. \cos 2, 1^{\circ} \\ \Rightarrow A B \approx 23, 96 (k m) \end{array}$

Vậy khoảng cách giữa hai tòa nhà là 23,96 km.

Bài 9 trang 79 Toán lớp 10: Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc $\hat{B P A} = 35^{o}$ và $\hat{B Q A} = 48^{o}$ . Tính chiều cao của tháp hải đăng đó.

Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B

Phương pháp giải:

Bước 1: Tính AB theo QB, dựa vào tan góc P và Q.

Bước 2: Lập phương trình, tìm QB.

Bước 3: Tính AB: $A B = Q B . \tan 48^{\circ}$

Lời giải:

Xét tam giác APB và AQB, ta có:

$\tan 35^{\circ} = \frac{A B}{P B} = \frac{A B}{300 + Q B}$ và $\tan 48^{\circ} = \frac{A B}{Q B}$

$\begin{array}{l} \Rightarrow A B = \tan 35^{\circ} . (300 + Q B) = \tan 48^{\circ} . Q B \\ \Leftrightarrow \tan 35^{\circ} .300 + \tan 35^{\circ} . Q B = \tan 48^{\circ} . Q B \\ \Leftrightarrow \tan 35^{\circ} .300 = (\tan 48^{\circ} - \tan 35^{\circ}) . Q B \\ \Leftrightarrow Q B = \frac{\tan 35^{\circ} .300}{\tan 48^{\circ} - \tan 35^{\circ}} \end{array}$

Mà $A B = \tan 48^{\circ} . Q B$

$\Rightarrow A B = \tan 48^{\circ} . \frac{\tan 35^{\circ} .300}{\tan 48^{\circ} - \tan 35^{\circ}} \approx 568, 5 (m)$

Vậy tháp hải đăng cao khoảng 568,5 m.

Bài 10 trang 79 Toán lớp 10: Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được $\hat{D A_{1} C_{1}} = 49^{o}, \hat{D B_{1} C_{1}} = 35^{o}$ . Tính chiều cao CD của tháp.

Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất

Phương pháp giải:

Bước 1: Tính góc $\hat{A_{1} D B_{1}}$ => Áp dụng định lí sin trong tam giác $A_{1} D B_{1}$ để tính $A_{1} D$

Bước 2: Tính $C_{1} D$ từ đó suy ra chiều cao của tháp.

Lời giải:

Ta có: $\hat{D A_{1} C_{1}} = \hat{A_{1} D B_{1}} + \hat{D B_{1} A_{1}} \Rightarrow \hat{A_{1} D B_{1}} = 49^{\circ} - 35^{\circ} = 14^{\circ}$

Áp dụng định lí sin trong tam giác $A_{1} D B_{1}$ , ta có:

$\begin{array}{l} \frac{A_{1} D}{\sin B_{1}} = \frac{A_{1} B_{1}}{\sin D} \Leftrightarrow \frac{A_{1} D}{\sin 35^{\circ}} = \frac{12}{\sin 14^{\circ}} \\ \Rightarrow A_{1} D = \sin 35^{\circ} . \frac{12}{\sin 14^{\circ}} \approx 28, 45 \end{array}$

Áp dụng định lí sin trong tam giác $A_{1} D C_{1}$ , ta có:

$\begin{array}{l} \frac{A_{1} D}{\sin C_{1}} = \frac{C_{1} D}{\sin A_{1}} \Leftrightarrow \frac{28, 45}{\sin 90^{\circ}} = \frac{C_{1} D}{\sin 49^{\circ}} \\ \Rightarrow C_{1} D = \sin 49^{\circ} . \frac{28, 45}{\sin 90^{\circ}} \approx 21, 47 \end{array}$