Bài 1 trang 78 Toán 10 Tập 1 | Chân trời sáng tạo Giải Toán lớp 10

Nguyễn Linh Anh Ngày: 24-08-2024 Lớp 10

2 K

Với giải Bài 1 trang 78 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 4 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương 4

Bài 1 trang 78 Toán lớp 10: Cho tam giác ABC. Biết a = 49,4; b = 26,4; $\hat{C} = 47 ° 20'$ . Tính hai góc $\hat{A}, \hat{B}$ và cạnh c.

Phương pháp giải:

Bước 1: Tính cạnh c: Áp dụng định lí cosin: $c^{2} = b^{2} + a^{2} - 2 a b \cos C$

Bước 2: Tính hai góc $\hat{A}, \hat{B}$ : Áp dụng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lời giải:

Áp dụng định lí cosin trong tam giác ABC, ta có: $\begin{array}{l} c^{2} = b^{2} + a^{2} - 2 a b \cos C \\ \Leftrightarrow c^{2} = 26, 4^{2} + 49, 4^{2} - 2.26, 4.49, 4 \cos 47^{\circ} 20^{'} \\ \Rightarrow c \approx 37 \end{array}$

Áp dụng định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

$\begin{array}{l} \Leftrightarrow \frac{49, 4}{\sin A} = \frac{26, 4}{\sin B} = \frac{37}{\sin 47^{\circ} 20^{'}} \\ \Rightarrow \sin A = \frac{49, 4. \sin 47^{\circ} 20^{'}}{37} \approx 0, 982 \Rightarrow \hat{A} \approx 79^{\circ} \\ \Rightarrow \hat{B} \approx 180^{\circ} - 79^{\circ} - 47^{\circ} 20^{'} = 53^{\circ} 40^{'} \end{array}$

Bài tập vận dụng:

Bài 1. Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số $\frac{R}{r} .$
Hướng dẫn giải

Giả sử AB = AC = a.

Xét tam giác ABC vuông cân tại A, theo định lí Pythagore ta có:

BC² = AB² + AC² = a² + a² = 2a²

$\Rightarrow B C = a \sqrt{2} .$

Do đó nửa chu vi tam giác ABC là

$p = \frac{A B + A C + B C}{2} = \frac{a + a + a \sqrt{2}}{2} = a . (\frac{2 + \sqrt{2}}{2})$

Tam giác ABC vuông tại A nên diện tích tam giác ABC là:

$S = \frac{1}{2} . A B . A C = \frac{1}{2} . a . a = \frac{a^{2}}{2}$

Mặt khác $S = p r = \frac{A B . A C . B C}{4 R}$

$\Rightarrow r = \frac{S}{p} = \frac{\frac{a^{2}}{2}}{a . (\frac{2 + \sqrt{2}}{2})} = \frac{a}{2 + \sqrt{2}}$ và

$R = \frac{A B . A C . B C}{4 S} = \frac{a . a . a \sqrt{2}}{4. \frac{a^{2}}{2}} = \frac{a \sqrt{2}}{2}$

Do đó $\frac{R}{r} = \frac{\frac{a \sqrt{2}}{2}}{\frac{a}{2 + \sqrt{2}}} = \frac{a \sqrt{2}}{2} : \frac{a}{2 + \sqrt{2}} = \frac{a \sqrt{2}}{2} . \frac{2 + \sqrt{2}}{a} = 1 + \sqrt{2}$

Vậy $\frac{R}{r} = 1 + \sqrt{2} .$

Bài 2. Nhà thầu đất Đức đã được cung cấp các kích thước sau đây qua điện thoại: Khu vườn hình tam giác ABC có $\hat{C A B} = 45 °$ , AC = 8 m, BC = 6 m. Nền đất cần phải có độ cao 10 cm.

a) Giải thích tại sao nhà thầu đất Đức cần thêm thông tin từ khách hàng của mình.

b) Cần khối lượng đất tối đa là bao nhiêu (để tạo thành nền của khu đất) nếu khách hàng của anh Đức không thể cung cấp thêm thông tin cần thiết?

Hướng dẫn giải

a) Áp dụng định lí sin với tam giác ABC ta có: $\frac{B C}{\sin \hat{C A B}} = \frac{A C}{\sin \hat{C B A}}$

$\Rightarrow \sin \hat{C B A} = \frac{A C . \sin \hat{C A B}}{B C} = \frac{8. \sin 45 °}{6} \approx 0, 943$

$\Rightarrow \hat{C B A} \approx 70 ° 34'$ hoặc $\hat{C B A} \approx 180 ° - 70 ° 34' \approx 109 ° 26'$ (hình vẽ dưới đây)

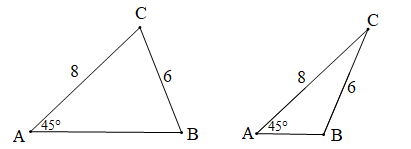Như vậy ta có thể có hai gá trị khác nhau của góc CBA nên hình tam giác không được xác định một cách duy nhất.

Điều đó giải thích tại sao anh Đức cần thêm thông tin về khu vườn.

b) Nền đất của khu vườn là một khối lăng trụ đứng với đáy là tam giác ABC và chiều cao không đổi là 10 cm, nên khối lượng đất tối đa để tạo ra nền của khu đất tỉ lệ với diện tích lớn nhất của tam giác ABC.

+) Nếu $\hat{C B A} \approx 70 ° 34'$ thì $\hat{A C B} \approx 180 ° - 45 ° - 70 ° 34' \approx 64 ° 26' .$

Khi đó diện tích của tam giác ABC là:

$S = \frac{1}{2} . C A . C B . \sin \hat{A C B} \approx \frac{1}{2} .8.6. \sin 64 ° 26' \approx 21, 65$ (m²)

+) Nếu $\hat{C B A} \approx 109 ° 26'$ thì $\hat{A C B} \approx 180 ° - 45 ° - 109 ° 26' \approx 25 ° 34' .$

Khi đó diện tích của tam giác ABC là:

$S = \frac{1}{2} . C A . C B . \sin \hat{A C B} \approx \frac{1}{2} .8.6. \sin 26 ° 34' \approx 10, 36$ (m²)

Khi đó diện tích lớn nhất của tam giác ABC là 21,65 m².

Đổi 10 cm = 0,1 m.

Khối lượng đất tối đa cần khoảng: 21,65. 0,1 ≈ 2,165 (m³)

Vậy khối lượng đất tối đa cần để tạo thành nền của khu đất khoảng 2,165 m³.

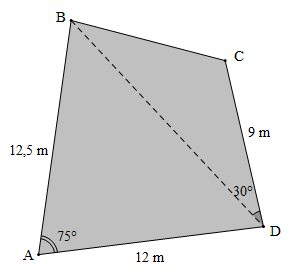
Bài 3. Vợ chồng anh Minh đang xem xét mua một mảnh đất. Nhân viên nhà đất cung cấp cho họ một bản vẽ chi tiết như hình vẽ dưới. Tính diện tích của mảnh đất và số tỉ đồng vợ chồng anh Minh cần dùng để mua đất biết giá đất là 25 triệu đồng/ m² đất (làm tròn kết quả đến chữ số thập phân thứ hai).