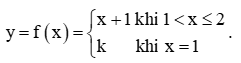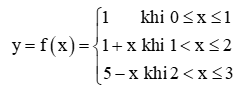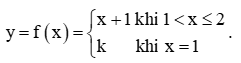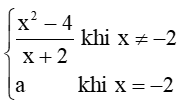Với giải Hoạt động khám phá 2 trang 81 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Hàm số liên tục giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 3: Hàm số liên tục
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số 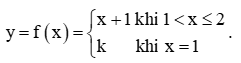 .
.
a) Xét tính liên tục của hàm số tại mỗi điểm x0 ∈ (1; 2).
b) Tìm và so sánh giá trị này với f(2).
c) Với giá trị nào của k thì ?
Lời giải:
a) Tại mỗi điểm x0 ∈ (1; 2) thì f(x) = x + 1
Khi đó: và f(x0) = x0 + 1
Suy ra
Vì vậy hàm số liên tục tại x0.
b) Tại x0 = 2 ta có f(x) = x + 1, khi đó:
f(2) = 2 + 1 = 3
Vậy
c) +) Tại x0 = 1 ta có f(x0) = k;
+) Tại x0 = 1
Dãy (xn) bất kì thỏa mãn 1 < xn ≤ 2 và xn → 1 thì f(xn) = xn + 1 khi đó .
Suy ra
Để thì k = 2.
Lý thuyết Hàm số liên tục trên một khoảng, trên một đoạn
- Hàm số xác định trên khoảng
Hàm số được gọi là liên tục trên khoảng nếu nó liên tục tại mọi điểm thuộc khoảng này.
- Hàm số được gọi là liên tục trên đoạn nếu nó liên tục trên khoảng và .
* Nhận xét:
- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn đó.
- Nếu hàm số liên tục trên đoạn và thì phương trình có ít nhất một nghiệm trên khoảng .
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khởi động trang 80 Toán 11 Tập 1: Hai đồ thị ở hai hình dưới đây cho biết phí gửi xe y của ô tô con (tính theo 10 nghìn đồng) theo thời gian gửi x (tính theo giờ) của hai bãi xe. Có nhận xét gì về sự thay đổi của số tiền phí phải trả theo thời gian gửi ở mỗi bãi đỗ xe?...
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 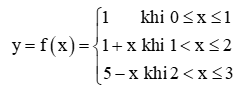 có đồ thị như Hình 1.....
có đồ thị như Hình 1.....
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số:...
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số 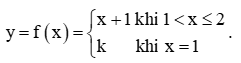 .....
.....
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2]....
Vận dụng 1 trang 82 Toán 11 Tập 1: Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau:...
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = ....
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số .....
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 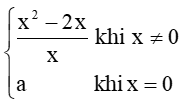 . Tìm a để hàm số y = f(x) liên tục trên ℝ.....
. Tìm a để hàm số y = f(x) liên tục trên ℝ.....
Vận dụng 2 trang 83 Toán 11 Tập 1: Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:...
Hoạt động khám phá 4 trang 83 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = . Hàm số y = f(x) + g(x) có liên tục tại x = 2 không? Giải thích....
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:.....
Vận dụng 3 trang 84 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Một đường thẳng d thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm M có hoành độ x (– 1 < x < 1) và cắt đường tròn (C) tại các điểm N và P (xem Hình 6)....
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:....
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 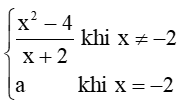 . Tìm a để hàm số f(x) liên tục trên ℝ....
. Tìm a để hàm số f(x) liên tục trên ℝ....
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:...
Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x) = . Xét tính liên tục của hàm số y = f(x).g(x) và y = ....
Bài 5 trang 85 Toán 11 Tập 1: Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:..
Bài 6 trang 85 Toán 11 Tập 1: Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = 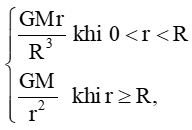 trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?....
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?....
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục
Bài tập cuối chương 3