Với giải Thực hành 4 trang 47 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 1: Hàm số và đồ thị học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 1: Hàm số và đồ thị
Thực hành 4 trang 47 Toán lớp 10:
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
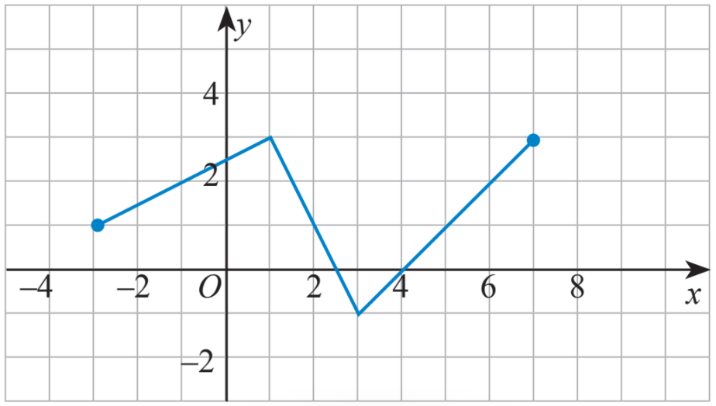
b) Xét tính đồng biến, nghịch biến của hàm số trên khoảng (2; 5).
Phương pháp giải:
a) Quan sát đồ thị trên các khoảng (-3; 1), (1;3), (3;7)
Khi hàm số đồng biến trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải.
Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
b)
Bước 1: Lấy là hai số tùy ý sao cho .
Bước 2: So sánh và
Bước 3: Kết luận tính đồng biến, nghịch biến
+ Nếu thì hàm số đồng biến trên khoảng (2; 5)
+ Nếu thì hàm số nghịch biến trên khoảng (2; 5)
Lời giải:
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thì có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thì có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thì có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số trên khoảng (2; 5).
Lấy là hai số tùy ý sao cho .
Do và nên , suy ra hay
Từ đây suy ra
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Lý thuyết Hàm số đồng biến, hàm số nghịch biến
- Với hàm số y = f(x) xác định trên khoảng (a; b), ta nói:
+ Hàm số đồng biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x1 < x2 ⇒ f(x1) < f(x2).
+ Hàm số nghịch biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x1 < x2 ⇒ f(x1) > f(x2).
Nhận xét:
+ Khi hàm số đồng biến (tăng) trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
Ví dụ:
+ Cho hàm số y = f(x) = 2x – 1 xác định trên ℝ.
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = 2.1 – 1 = 1.
f(x2) = f(2) = 2.2 – 1 = 3.
Ta thấy x1 < x2 và f(x1) < f(x2) nên hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ.
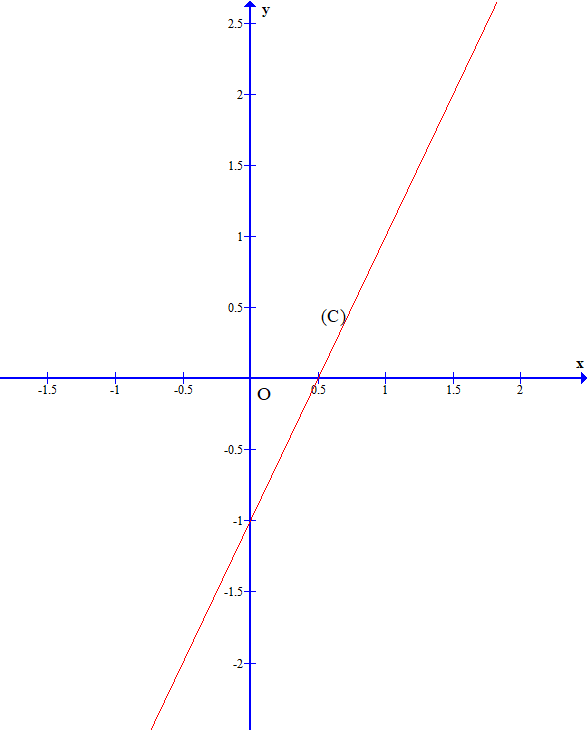
Ta thấy hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ nên đồ thị của nó có dạng đi lên từ trái sang phải.
+ Cho hàm số y = f(x) = ‒ x + 2 xác định trên ℝ.
Xét 2 giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = ‒1 + 2 = 1.
f(x2) = f(2) = ‒ 2 + 2 = 0.
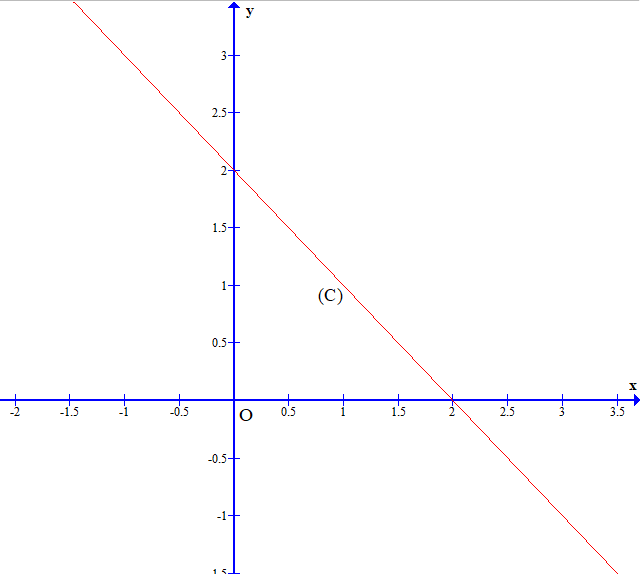
Ta thấy x1 < x2 và f(x1) > f(x2) nên hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ.
Ta thấy hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ nên đồ thị của nó có dạng đi xuống từ trái sang phải.
Ví dụ: Cho hàm số y = f(x) có tập xác định là [‒3; 3] và có đồ thị hàm số như hình vẽ.
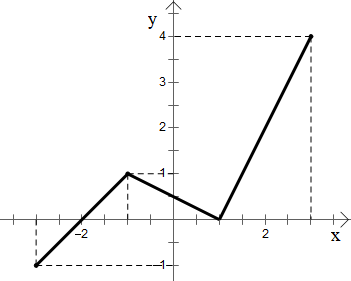
Tìm khoảng đồng biến, nghịch biến của hàm số trên.
Hướng dẫn giải
Dựa vào đồ thị nhận thấy:
- Đồ thị hàm số có dạng đi lên từ trái sang phải trên các khoảng (‒3; ‒1) và (1; 3) nên hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);
- Đồ thị hàm số có dạng đi xuống từ trái sang phải trên khoảng (‒1; 1) nên hàm số nghịch biến trên khoảng (‒1; 1).
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khởi động trang 41 Toán lớp 10: Nhiệt độ có mối liên hệ gì với thời gian?...
Thực hành 2 trang 43 Toán lớp 10: Tìm tập xác định của các hàm số sau:...
HĐ Khám phá 2 trang 43 Toán lớp 10: Xét hàm số y=f(x) cho bởi bảng sau:...
Thực hành 3 trang 44 Toán lớp 10: Vẽ đồ thị hàm số f(x)=3x+8...
Bài 1 trang 47 Toán lớp 10: Tìm tập xác định của các hàm số sau:...
Bài 2 trang 47 Toán lớp 10: Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10...
Bài 3 trang 47 Toán lớp 10: Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:...
Bài 4 trang 47 Toán lớp 10: Vẽ đồ thị hàm số f(x)=|x| biết rằng hàm số này còn được viết như sau:...
Bài 5 trang 48 Toán lớp 10: Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:...
Bài 6 trang 48 Toán lớp 10: Một hãng taxi có bảng giá như sau:...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 00 đến 1800