Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 1: Mệnh đề chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 1: Mệnh đề  

Video bài giảng Mệnh đề - Chân trời sáng tạo

Giải toán lớp 10 trang 7 Tập 1 Chân trời sáng tạo

HĐ Khởi động trang 7 Toán lớp 10:Bạn có thể phát biểu định lí theo cách khác?

Phương pháp giải:

Định lí trên bảng là một mệnh đề kéo theo, nên có thể phát biểu dạng:

“Nếu P thì Q”, “P suy ra Q”, “P kéo theo Q”, hoặc sử dụng cụm “điều kiện cần”, “điều kiện đủ”

Lời giải:

Định lí có tóm tắt như trên bảng còn thể phát biểu là:

1. Tam giác ABC cân suy ra nó có hai góc ở đáy bằng nhau.

2. Tam giác ABC cân kéo theo nó có hai góc ở đáy bằng nhau.

3. Tam giác ABC cân là điều kiện đủ để nó có hai góc ở đáy bằng nhau.

4. Tam giác ABC có hai góc ở đáy bằng nhau là điều kiện cần để có tam giác ABC cân.

1. Mệnh đề

HĐ Khám phá 1 trang 7 Toán lớp 10: Xét các câu sau đây:

(1) 1+1=2.

(2) Dân ca Quan họ là di sản văn hóa phi vật thể đại diện của nhân loại.

(3) Dơi là một loài chim

(4) Nấm có phải là một loài thực vật không?

(5) Hoa hồng đẹp nhất trong các loài hoa.

(6) Trời ơi, nóng quá!

Trong những câu trên,

a) Câu nào là khẳng định đúng, câu nào là khẳng định sai?

b) Câu nào không phải là khẳng định?

c) Câu nào là khẳng định, nhưng không thể xác định nó đúng hay sai?

Lời giải:

a) Câu là khẳng định đúng:

(1) 1+1=2.

(2) Dân ca Quan họ là di sản văn hóa phi vật thể đại diện của nhân loại.

Câu là khẳng định sai:

(3) Dơi là một loài chim

b) Câu không phải là khẳng định:

(4) Nấm có phải là một loài thực vật không?

(6) Trời ơi, nóng quá!

c) Câu là khẳng định, nhưng không thể xác định nó đúng hay sai:

(5) Hoa hồng đẹp nhất trong các loài hoa.

Giải toán lớp 10 trang 8 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 8 Toán lớp 10: Trong các câu sau, câu nào là mệnh đề?

a) $\sqrt{2}$ là số vô tỉ

b) $\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{10}}>2$

c) 100 tỉ là số rất lớn

d) Trời hôm nay đẹp quá!

Phương pháp giải:

Mệnh đề là một khẳng định đúng hoặc sai.

Lời giải:

a) “$\sqrt{2}$ là số vô tỉ” là một mệnh đề (do là khẳng định đúng).

b) “$\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{10}}>2$” là một mệnh đề (do là khẳng định đúng).

c) “100 tỉ là số rất lớn” không là một mệnh đề (do là một khẳng định không đúng, không sai)

d) “Trời hôm nay đẹp quá!” không là một mệnh đề (do không là khẳng định).

Thực hành 2 trang 8 Toán lớp 10: Xét tính đúng sai của các mệnh đề sau:

a) Vịnh Hạ Long là di sản thiên nhiên thế giới.

b) $\sqrt{{(-5)}^2}=-5$

c) $5^2+{12}^2={13}^2$

Lời giải chi tiết:

a) “Vịnh Hạ Long là di sản thiên nhiên thế giới” là mệnh đề đúng.

b) “$\sqrt{{(-5)}^2}=-5$” là mệnh đề sai (vì $\sqrt{{(-5)}^2}=\left|-5\right|=5$).

c) “$5^2+{12}^2={13}^2$” là mệnh đề đúng (vì $5^2+{12}^2=169={13}^2$)

2. Mệnh đề chứa biến

HĐ Khám phá 2 trang 8 Toán lớp 10: Xét câu “n chia hết cho 5” (n là số tự nhiên).

a) Có thể khẳng định câu trên là đúng hay sai không?

b) Tìm hai giá trị của n sao cho câu trên là khẳng định đúng, hai giá trị của n sao cho câu trên là khẳng định sai.

Lời giải:

a) Không thể khẳng định câu trên là đúng hay sai.

b)

+) n = 0 hoặc n =5 thì “n chia hết cho 5” là khẳng định đúng.

+) n = 2 hoặc n =34 thì “n chia hết cho 5” là khẳng định sai.

Giải toán lớp 10 trang 9 Tập 1 Chân trời sáng tạo

Thực hành 3 trang 9 Toán lớp 10: Với mỗi mệnh đề chứa biến sau, tìm những giá trị của biến để nhận được một mệnh đề đúng và một mệnh đề sai.

a) $P(x):"x^2=2"$

b) $Q(x):"x^2+1>0"$

c)  $R(n):"n+2$ chia hết cho 3” (n là số tự nhiên).

Lời giải:

a)

+) $x=\sqrt{2}$ ta được mệnh đề  là một mệnh đề đúng.

+) $x=0$ ta được mệnh đề  là một mệnh đề sai.

b)

+) $x=0$ ta được mệnh đề  là một mệnh đề đúng.

+) Không có giá trị của x để  là một mệnh đề sai do $x^2+1>0$ với mọi x.

c)  chia hết cho 3” (n là số tự nhiên).

+) $n=1$ ta được mệnh đề  chia hết cho 3” là một mệnh đề đúng.

+) $n=5$ta được mệnh đề  chia hết cho 3” là một mệnh đề sai.

3. Mệnh đề phủ định

HĐ Khám phá 3 trang 9 Toán lớp 10: Xét các cặp mệnh đề nằm cùng dòng của bảng (có hai cột P và $\overline{P}$) sau đây:

P	$\overline{P}$
Dơi là một loài chim	Dơi không phải là một loài chim
$\pi$ không phải là một số hữu tỉ	$\pi$ là một số hữu tỉ
$\sqrt{2}+\sqrt{3}>\sqrt{5}$	$\sqrt{2}+\sqrt{3}\le \sqrt{5}$
$\sqrt{2}.\sqrt{18}=6$	$\sqrt{2}.\sqrt{18}\ne 6$

Lời giải:

P		$\overline{P}$
Dơi là một loài chim	Sai	Dơi không phải là một loài chim	Đúng
$\pi$ không phải là một số hữu tỉ	Đúng	$\pi$ là một số hữu tỉ	Sai
$\sqrt{2}+\sqrt{3}>\sqrt{5}$	Đúng	$\sqrt{2}+\sqrt{3}\le \sqrt{5}$	Sai
$\sqrt{2}.\sqrt{18}=6$	Đúng	$\sqrt{2}.\sqrt{18}\ne 6$	Sai

Chú ý:

Hai mệnh đề cùng cặp luôn có một mệnh đề đúng và một mệnh đề sai.

Nếu P đúng thì $\overline{P}$ sai và ngược lại.

Giải toán lớp 10 trang 10 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 10 Toán lớp 10: Phát biểu mệnh đề phủ định của các mệnh đề sau. Xét tính đúng sai của mỗi mệnh đề và mệnh đề phủ định của nó.

a) Paris là thủ đô của nước Anh

b) 23 là số nguyên tố

c) 2021 chia hết cho 3

d) Phương trình $x^2-3x+4=0$ vô nghiệm.

Phương pháp giải:

Để phủ định mệnh đề, ta thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề đó. Hoặc diễn đạt bằng từ ngữ, kí hiệu toán học đối lập.

Lời giải:

Mệnh đề phủ định của các mệnh đề trên là:

a) “Paris không phải là thủ đô của nước Anh”

b) “23 không phải là số nguyên tố”

c) “2021 không chia hết cho 3”

d) “Phương trình $x^2-3x+4=0$ có nghiệm”.

+) Xét tính đúng sai:

a) “Paris là thủ đô của nước Anh” là mệnh đề sai.

“Paris không phải là thủ đô của nước Anh” là mệnh đề đúng.

b) “23 là số nguyên tố” là mệnh đề đúng.

“23 không phải là số nguyên tố” là mệnh đề sai.

c) “2021 chia hết cho 3” là mệnh đề sai.

“2021 không chia hết cho 3” là mệnh đề đúng.

d) “Phương trình $x^2-3x+4=0$ vô nghiệm” là mệnh đề sai.

“Phương trình $x^2-3x+4=0$ có nghiệm” là mệnh đề đúng.

4. Mệnh đề kéo theo

HĐ Khám phá 4 trang 10 Toán lớp 10: Xét hai mệnh đề sau:

(1) Nếu ABC là tam giác đều thì nó là tam giác cân

(2) Nếu 2a – 4 > 0 thì a > 2

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Mỗi mệnh đề trên đều có dạng “Nếu P thì Q”. Chỉ ra P và Q ứng với mỗi mệnh đề đó.

Lời giải:

a)

(1) “Nếu ABC là tam giác đều thì nó là tam giác cân” là mệnh đề đúng.

(2) “Nếu 2a – 4 >0 thì a > 2” là mệnh đề đúng.

b) Trong mệnh đề (1) “Nếu ABC là tam giác đều thì nó là tam giác cân”

P: “ABC là tam giác đều”

Q: “ABC là tam giác cân”

Trong mệnh đề (2) “Nếu 2a – 4 > 0 thì a > 2”

P: “2a – 4 > 0”

Q: “a > 2”

Chú ý

Từ “nó” trong mênh đề (1) được hiểu là “ABC”. Do đó khi chỉ ra mệnh đề Q, ta dùng “ABC” thay cho “nó” để mệnh đề được rõ nghĩa.

Giải toán lớp 10 trang 12 Tập 1 Chân trời sáng tạo

Thực hành 5 trang 12 Toán lớp 10: Xét hai mệnh đề:

P: “Hai tam giác ABC và A’B’C’ bằng nhau”.

Q: “Hai tam giác ABC và A’B’C’ có diện tích bằng nhau”.

a) Phát biểu mệnh đề $P\Rightarrow Q$.

b) Mệnh đề $P\Rightarrow Q$ có phải là một định lí không? Nếu có, sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” để phát biểu định lí này theo cách khác nhau.

Phương pháp giải:

a) Mệnh đề $P\Rightarrow Q$ phát biểu là “Nếu P thì Q”

b) Khi mệnh đề $P\Rightarrow Q$ là một định lí, ta nói:

P là điều kiện đủ để có Q,

Q là điều kiện cần để có P.

Lời giải:

a) Mệnh đề $P\Rightarrow Q$: “Nếu hai tam giác ABC và A’B’C’ bằng nhau thì chúng có diện tích bằng nhau”

b) Mệnh đề $P\Rightarrow Q$ đúng nên nó là một định lí. Hai cách phát biểu định lí là:

Hai tam giác ABC và A’B’C’ bằng nhau là điều kiện đủ để có diện tích bằng nhau.

Hai tam giác ABC và A’B’C’ có diện tích bằng nhau là điều kiện cần để chúng bằng nhau.

5. Mệnh đề đảo. Hai mệnh đề tương đương

HĐ Khám phá 5 trang 12 Toán lớp 10: Xét hai mệnh đề dạng $P\Rightarrow Q$ sau:

“Nếu ABC là tam giác đều thì nó có hai góc bằng ${60}^o$”;

“Nếu $a=2$ thì $a^2-4=0$”.

a) Chỉ ra P, Q và xét tính đúng sai của mỗi mệnh đề trên.

b) Với mỗi mệnh đề đã cho, phát biểu mệnh đề $Q\Rightarrow P$ và xét tính đúng sai của nó.

Phương pháp giải:

Mệnh đề $Q\Rightarrow P$ phát biểu là “Nếu Q thì P”

Lời giải:

a)

+) Mệnh đề R: “Nếu ABC là tam giác đều thì nó có hai góc bằng ${60}^o$” có dạng $P\Rightarrow Q$, với

P: “ABC là tam giác đều” và Q: “Tam giác ABC có hai góc bằng ${60}^o$”

Ta thấy khi P đúng thì Q cũng đúng. Do đó $P\Rightarrow Q$ đúng hay R đúng.

+) Mệnh đề T: “Nếu $a=2$ thì $a^2-4=0$” có dạng $P\Rightarrow Q$, với:

P: “$a=2$” và Q: “$a^2-4=0$”.

Ta thấy khi P đúng thì Q cũng đúng. Do đó $P\Rightarrow Q$ đúng hay T đúng.

b) Mệnh đề $Q\Rightarrow P$ của hai mệnh đề trên là:

“Nếu ABC có hai góc bằng ${60}^o$ thì nó là tam giác đều”, đúng.

“Nếu $a^2-4=0$ thì $a=2$” sai (vì thiếu nghiệm $a=-2$).

Giải toán lớp 10 trang 13 Tập 1 Chân trời sáng tạo

Thực hành 6 trang 13 Toán lớp 10: Xét hai mệnh đề:

P: “Tứ giác ABCD là hình vuông”;

Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”.

a) Phát biểu mệnh đề $P\Rightarrow Q$ và mệnh đề đảo của nó.

b) Hai mệnh đề P và Q có tương đương không? Nếu có, sử dụng thuật ngữ “điều kiện cần và đủ” hoặc “khi và chỉ khi” để phát biểu định lí $P\iff Q$ theo hai cách khác nhau.

Phương pháp giải:

a)

Mệnh đề $P\Rightarrow Q$ phát biểu là “Nếu P thì Q”, “P kéo theo Q” hoặc “Từ P suy ra Q”.

Mệnh đề $Q\Rightarrow P$ phát biểu là “Nếu Q thì P”

b) Hai mệnh đề P và Q là tương đương nếu cả hai mệnh đề $P\Rightarrow Q$ và $Q\Rightarrow P$ đều đúng.

Phát biểu:

“P là điều kiện cần và đủ để có Q” (hoặc “Q là điều kiện cần và đủ để có P”)

Hoặc “P khi và chỉ chi Q”.

Lời giải:

a)

Mệnh đề $P\Rightarrow Q$: “Nếu tứ giác ABCD là hình vuông thì nó là hình chữ nhật có hai đường chéo vuông góc với nhau”

Mệnh đề $Q\Rightarrow P$: “Nếu tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau thì nó là hình vuông”

b)

Theo dấu hiệu nhận biết hình vuông, hai mệnh đề $P\Rightarrow Q$ và $Q\Rightarrow P$ đều đúng. Do đó, P và Q là hai mệnh đề tương đương. Ta có thể phát biểu thành định lí như sau:

 “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để nó là hình vuông”

Hoặc “Tứ giác ABCD là hình vuông khi và chỉ khi nó là hình chữ nhật có hai đường chéo vuông góc với nhau"

6. Mệnh đề chứa kí hiệu $\forall ,\exists$

HĐ Khám phá 6 trang 13 Toán lớp 10: Xét tính đúng sai của các mệnh đề sau:

(1) Với mọi số tự nhiên $x,\sqrt{x}$ là số vô tỉ;

(2) Bình phương của mọi số thực đều không âm;

(3) Có số nguyên cộng với chính nó bằng 0;

(4) Có số tự nhiên n sao cho 2n – 1 = 0.

Lời giải:

(1) “Với mọi số tự nhiên $x,\sqrt{x}$ là số vô tỉ” sai, chẳng hạn $x=1:\sqrt{x}=1$ không là số vô tỉ.

(2) “Bình phương của mọi số thực đều không âm” đúng;

(3) “Có số nguyên cộng với chính nó bằng 0” đúng, số nguyên đó chính là số 0;

(4) “Có số tự nhiên n sao cho 2n – 1 = 0” sai, vì chỉ khi $n=\frac{1}{2}$ thì 2n – 1 = 0 nhưng $\frac{1}{2}$ không phải là số tự nhiên.

Giải toán lớp 10 trang 14 Tập 1 Chân trời sáng tạo

Thực hành 7 trang 14 Toán lớp 10: Sử dụng kí hiệu $\mathrm{\forall },\mathrm{\exists }$ để viết các mệnh đề sau:

a) Mọi số thực cộng với số đối của nó đều bằng 0

b) Có một số tự nhiên mà bình phương bằng 9.

Lời giải:

a) “$\mathrm{\forall }x\in \mathbb{R},x+(-x)=0$”

b) “$\mathrm{\exists }n\in \mathbb{N},x^2=9$”

Thực hành 8 trang 14 Toán lớp 10: Xét tính đúng sai và viết mệnh đề phủ định của các mệnh đề sau:

a) $\mathrm{\forall }x\in \mathbb{R},x^2>0$

b) $\mathrm{\exists }x\in \mathbb{R},x^2=5x-4$

c) $\mathrm{\exists }x\in \mathbb{Z},2x+1=0$

Phương pháp giải:

Phủ định của mệnh đề “$\mathrm{\forall }x\in X,P(x)$” là “$\mathrm{\exists }x\in X,\overline{P(x)}$”

Phủ định của mệnh đề “$\mathrm{\exists }x\in X,P(x)$” là “$\mathrm{\forall }x\in X,\overline{P(x)}$”

Lời giải:

a) Mệnh đề sai, vì $x=0\in \mathbb{R}$ nhưng $0^2$ không lớn hơn 0.

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\exists }x\in \mathbb{R},x^2\le 0$”

b) Mệnh đề đúng, vì $x=1\in \mathbb{R}$ thỏa mãn $1^2=5.1-4$

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\forall }x\in \mathbb{N},x^2\ne 5x-4$”

 c) Mệnh đề sai, vì $2x+1=0\iff x=-\frac{1}{2}\notin \mathbb{Z}$

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\forall }x\in \mathbb{Z},2x+1\ne 0$”

Bài tập

Bài 1 trang 14 Toán lớp 10: Trong các khẳng định sau, khẳng định nào là mệnh đề, khẳng định nào là mệnh đề chứa biến

a) $3+2>5$

b) $1-2x=0$

c) $x-y=2$

d) $1-\sqrt{2}<0$

Lời giải:

Các khẳng định là mệnh đề là:

a) $3+2>5$

d) $1-\sqrt{2}<0$

Các khẳng định là mệnh đề chứa biến là:

b) $1-2x=0$

c) $x-y=2$

Bài 2 trang 14 Toán lớp 10: Xét tính đúng sai của các mệnh đề sau và phát biểu mệnh đề phủ định của chúng.

a) 2020 chia hết cho 3

b) $\pi <3,15$

c) Nước ta hiện nay có 5 thành phố trực thuộc trung ương.

d) Tam giác có hai góc bằng ${45}^o$ là tam giác vuông cân.

Lời giải:

a) Mệnh đề “2020 chia hết cho 3” sai.

Mệnh đề phủ định của mệnh đề này là: “2020 không chia hết cho 3”

b) Mệnh đề “$\pi <3,15$” đúng vì $\pi \approx 3,141592654$

Mệnh đề phủ định của mệnh đề này là: “$\pi \ge 3,15$”

c) Mệnh đề “Nước ta hiện nay có 5 thành phố trực thuộc trung ương” đúng (gồm Hà Nội, Đà Nẵng, Hải Phòng, Hồ Chí Minh và Cần Thơ)

Mệnh đề phủ định của mệnh đề này là: “Nước ta hiện nay không phải có 5 thành phố trực thuộc trung ương”

d) Mệnh đề “Tam giác có hai góc bằng ${45}^o$ là tam giác vuông cân” đúng.

Mệnh đề phủ định của mệnh đề này là: “Tam giác có hai góc bằng ${45}^o$ không phải là tam giác vuông cân”

Bài 3 trang 14 Toán lớp 10: Xét hai mệnh đề:

P: “Tứ giác ABCD là hình bình hành”.

Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.

a) Phát biểu mệnh đề $P\Rightarrow Q$ và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề $P\Rightarrow Q$.

Lời giải:

a) Mệnh đề $P\Rightarrow Q$: “Nếu tứ giác ABCD là hình bình hành thì nó có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.

Mệnh đề này đúng vì “hai đường chéo cắt nhau tại trung điểm của mỗi đường” là tính chất của hình hình hành.

b) Mệnh đề đảo của mệnh đề $P\Rightarrow Q$ là mệnh đề $Q\Rightarrow P$, được phát biểu là: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì nó là hình bình hành”.

Giải toán lớp 10 trang 15 Tập 1 Chân trời sáng tạo

Bài 4 trang 15 Toán lớp 10: Cho các định lí:

P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.

Q: “Nếu $a<b$ thì $a+c<b+c$” ($a,b,c\in \mathbb{R}$).

a) Chỉ ra giả thiết và kết luận của mỗi định lí.

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.

c) Mệnh đề đảo của mỗi định lí đó có là định lí không?

Lời giải:

a)

Mệnh đề P có dạng $R\Rightarrow T$với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”

Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”

Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”

Mệnh đề Q có dạng $A\Rightarrow B$với A: “$a<b$” và B: “$a+c<b+c$”

Giả thiết là mệnh đề A: “$a<b$”

Kết luận là mệnh đề B: “$a+c<b+c$”

b)

+) Mệnh đề P có thể phát biểu lại như sau:

Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.

Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.

+) Mệnh đề Q có thể phát biểu lại như sau:

$a<b$ là điều kiện đủ để có $a+c<b+c$.

$a+c<b+c$là điều kiện cần để có $a<b$.

c)

Mệnh đề đảo của mệnh đề P có dạng $T\Rightarrow R$, phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.

Mệnh đề này sai nên không là định lí.

Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.

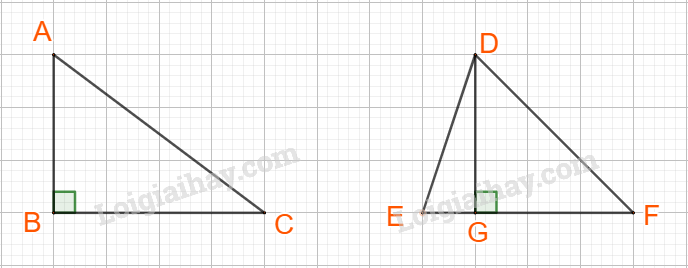
Mệnh đề đảo của mệnh đề Q có dạng $B\Rightarrow A$, phát biểu là: “Nếu $a+c<b+c$thì $a<b$”.

Mệnh đề này đúng nên nó cũng là định lí.

Bài 5 trang 15 Toán lớp 10: Sử dụng thuật ngữ “điều kiện cần và đủ”, phát biểu lại các định lí sau:

a) Một phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.

b) Một hình bình hành là hình thoi thì nó có hai đường chéo vuông góc với nhau và ngược lại.

Lời giải:

Các định lí trên có thể được phát biểu là:

a) Một phương trình bậc hai có biệt thức dương là điều kiện cần và đủ để có hai nghiệm phân biệt

b) Một hình bình hành có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để nó là hình thoi.

Bài 6 trang 15 Toán lớp 10: Cho các mệnh đề sau:

P: “Giá trị tuyệt đối của mọi số thực đều lớn hơn hoặc bằng chính nó”

Q: “Có số tự nhiên sao cho bình phương của nó bằng 10”

R: “Có số thực x sao cho $x^2+2x-1=0$”

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Sử dụng kí hiệu $\mathrm{\forall },\mathrm{\exists }$ để viết lại các mệnh đề đã cho.

Lời giải:

a) Mệnh đề P đúng, vì: $\left|x\right|=\{\begin{array}{l}x(x\ge 0)\\ -x(x<0)\end{array}$ nên $\left|x\right|\ge x$.

Mệnh đề Q sai vì chỉ có các số $\pm \sqrt{10}$ có bình phương bằng 10, nhưng $\sqrt{10}$ và $-\sqrt{10}$ đều không là số tự nhiên.

Mệnh đề R đúng vì $x=-1+\sqrt{2}\in \mathbb{R}$ thỏa mãn $x^2+2x-1=0.$

b) Có thể viết lại các mệnh đề trên như sau:

P: “$\mathrm{\forall }x\in \mathbb{R},\left|x\right|\ge x$”

Q: “$\mathrm{\exists }n\in \mathbb{N},n^2=10$”

R: “$\mathrm{\exists }x\in \mathbb{R},x^2+2x-1=0$”

Bài 7 trang 15 Toán lớp 10: Xét tính đúng sai và viết mệnh đề phủ định của các mệnh đề sau đây:

a) $\mathrm{\exists }x\in \mathbb{N},x+3=0$

b) $\mathrm{\forall }x\in \mathbb{R},x^2+1\ge 2x$

c) $\mathrm{\forall }a\in \mathbb{R},\sqrt{a^2}=a$

Lời giải:

a) Mệnh đề sai, vì chỉ có $x=-3$ thảo mãn $x+3=0$nhưng $-3\notin \mathbb{N}$.

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\forall }x\in \mathbb{N},x+3\ne 0$”.

b) Mệnh đề đúng, vì  $(x-1{)}^2\ge 0$ hay$x^2+1\ge 2x$ với mọi số thực x.

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\exists }x\in \mathbb{R},x^2+1<2x$”

 c) Mệnh đề sai, vì có $a=-2\in \mathbb{R},\sqrt{{(-2)}^2}=2\ne a$

Mệnh đề phủ định của mệnh đề này là: “$\mathrm{\exists }a\in \mathbb{R},\sqrt{a^2}\ne a$”.

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tập hợp

Bài 3: Các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn