Cho ∆1 và ∆2. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là

Cho ∆1 và ∆2. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là

Thanh Dung Ngày: 05-01-2023 Lớp 10

655

Với giải Bài 38 trang 82 SBT Toán lớp 10 Cánh diều chi tiết trong Bài 4: Vị trí tương đối của góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 4: Vị trí tương đối của góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

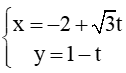
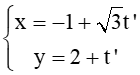
Bài 38 trang 82 SBT Toán 10 Tập 2: Cho $Δ_{1}$ : Cho ∆1 x = -2+(căn3)t; y = 1-t và ∆2 x = -1+(căn3)t'; y = 2+t' và $∆_{2}$ :. Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰;

B. 45⁰;

C. 90⁰;

D. 60⁰.

Lời giải:

Ta thấy vectơ chỉ phương của ∆₁ là: $\vec{u_{1}}$ =( $\sqrt{3}$ ;-1)

Vectơ chỉ phương của ∆₂ là: $\vec{u_{2}}$ =( $\sqrt{3}$ ;1)

Ta có: cos( $\vec{u_{1}}$ , $\vec{u_{2}}$ ) = Cho ∆1 x = -2+(căn3)t; y = 1-t và ∆2 x = -1+(căn3)t'; y = 2+t'

Suy ra góc giữa 2 đường thẳng chính là góc nhọn giữa 2 vectơ chỉ phương của 2 đường thẳng đó.

Do đó $(Δ_{1}, Δ_{2}) = (\vec{u_{1}}, \vec{u_{2}}) = 60^{o}$

Vậy chọn đáp án D.

Xem thêm lời giải SBT Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 33 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng song song với đường thẳng x – 2y + 3 = 0?...

Bài 34 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng vuông góc với đường thẳng ?...

Bài 35 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(- 1; 2) và song song với đường thẳng d: 2x – y – 5 = 0 có phương trình tổng quát là:...

Bài 36 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(3; - 4) và vuông góc với đường thẳng d: x – 3y + 1 = 0 có phương trình tổng quát là:...

Bài 37 trang 81 SBT Toán 10 Tập 2: Cho ∆₁: x – 2y + 3 = 0 và ∆₂: – 2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:...

Bài 38 trang 82 SBT Toán 10 Tập 2: Cho :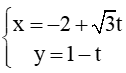 Cho ∆1 x = -2+(căn3)t; y = 1-t và ∆2 x = -1+(căn3)t'; y = 2+t' và :. Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:...

Bài 39 trang 82 SBT Toán 10 Tập 2: Khoảng cách từ điểm M(5; - 2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:...

Bài 40 trang 82 SBT Toán 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau:...

Bài 41 trang 82 SBT Toán 10 Tập 2: Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:...

Bài 42 trang 82 SBT Toán 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:...

Bài 43 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng song song ∆₁: ax + by + c = 0 và ∆₂: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆₁ và ∆₂ bằng ...

Bài 44 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng ∆₁: mx – 2y – 1 = 0 và ∆₂: x – 2y + 3 = 0. Với giá trị nào của tham số m thì:...

Bài 45 trang 82 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B đồng thời cách đều A và C?...

Bài 46 trang 83 SBT Toán 10 Tập 2: Có hai tàu điện ngầm A và B chạy trong nội đô thành phố cùng xuất phát từ hai ga, chuyển động đều theo đường thẳng. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), sau khi xuất phát t (giờ) (t ≥ 0), vị trí của tàu A có tọa độ được xác định bởi công thức Có hai tàu điện ngầm A và B chạy trong nội đô thành phố cùng xuất phát từ hai ga , vị trí của tàu B có tọa độ là (9 + 8t; 5 – 36t)...

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

SBT Toán 10 Bài 3: Phương trình đường thẳng

SBT Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

SBT Toán 10 Bài 5: Phương trình đường tròn

SBT Toán 10 Bài 6: Ba đường conic

SBT Toán 10 Bài tập cuối chương 7

Từ khóa :

toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

144

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

120

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

107

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

100

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.